Learn
AI & Machine Learning

Local Sensitivity Hashing (L.S.H.): A Comprehensive Guide

Mar 30, 20247 min read

Local Sensitivity Hashing (LSH) is a pivotal technique for tackling the complexities of large, high-dimensional datasets, streamlining the process of similarity search and data retrieval.

By Shanika W.

Read the entire series

In the era of big data and machine learning, efficiently finding nearest neighbors or similar items in large, high-dimensional datasets is a fundamental challenge across many applications. Take a music streaming service like Spotify, for example. To provide personalized song recommendations, it needs to quickly identify tracks most similar to a user’s preferences from a massive library of millions of songs, each represented by hundreds of attributes like audio features, lyrics, genres, etc. This is a high-dimensional approximate nearest-neighbor search problem.

Traditional techniques like linear scans, space-partitioning tree methods, or hash tables become computationally prohibitive as the number of dimensions and data points increases. This is where an approach called Locality Sensitive Hashing (LSH) and, sometimes, hash-based indexes comes into play. LSH is an approximate technique that can drastically enhance the efficiency of similarity search in high dimensions by intelligently mapping similar data points to the same buckets or locations with high probability. This allows you to explore only a small subset of candidates instead of exhaustively comparing against the entire dataset.

The Essence and Challenges of Similarity Search in High Dimensional Data

Similarity or vector similarity search is a technique in information retrieval and data-driven applications. The goal is to identify items or data points resembling a given query vector by comparing their spatial distance in the high-dimensional space.

This technique plays a role across numerous use cases. For instance, in e-commerce, similarity search powers product recommendation engines, offering customers choices aligned with their preferences, thereby enriching the shopping experience. In multimedia services, it enables retrieving images, videos, or music that resonate with specific patterns or themes, enhancing content discoverability and user engagement. However, similarity search presents significant computational challenges, particularly in handling large and high-dimensional datasets. Traditional brute-force methods compare each data point with every other point, impractically time-consuming due to their quadratic time complexity, especially in big data contexts. Consequently, we need an efficient approach to swiftly pinpoint similar items without requiring exhaustive pairwise comparisons, streamlining the search process in extensive datasets. Locality Sensitive Hashing (LSH) addresses this by increasing the likelihood of hash value collisions for similar inputs, grouping them into hash bins and thus improving the efficiency of similarity searches.

What is Locality-Sensitive Hashing (LSH)?

Locality-Sensitive Hashing (LSH), introduced by Indyk-Motwani in 1998, is a technique used in approximate nearest neighbor (ANN) searches that underpins and accelerates the efficiency of similarity searches. Unlike conventional hashing, which mainly focuses on mapping each data point, LSH groups similar data points together. This is enabled by its “locality sensitivity,” which ensures that close points in the original data spaces would end up in the same location, also referred to as a “bucket.”

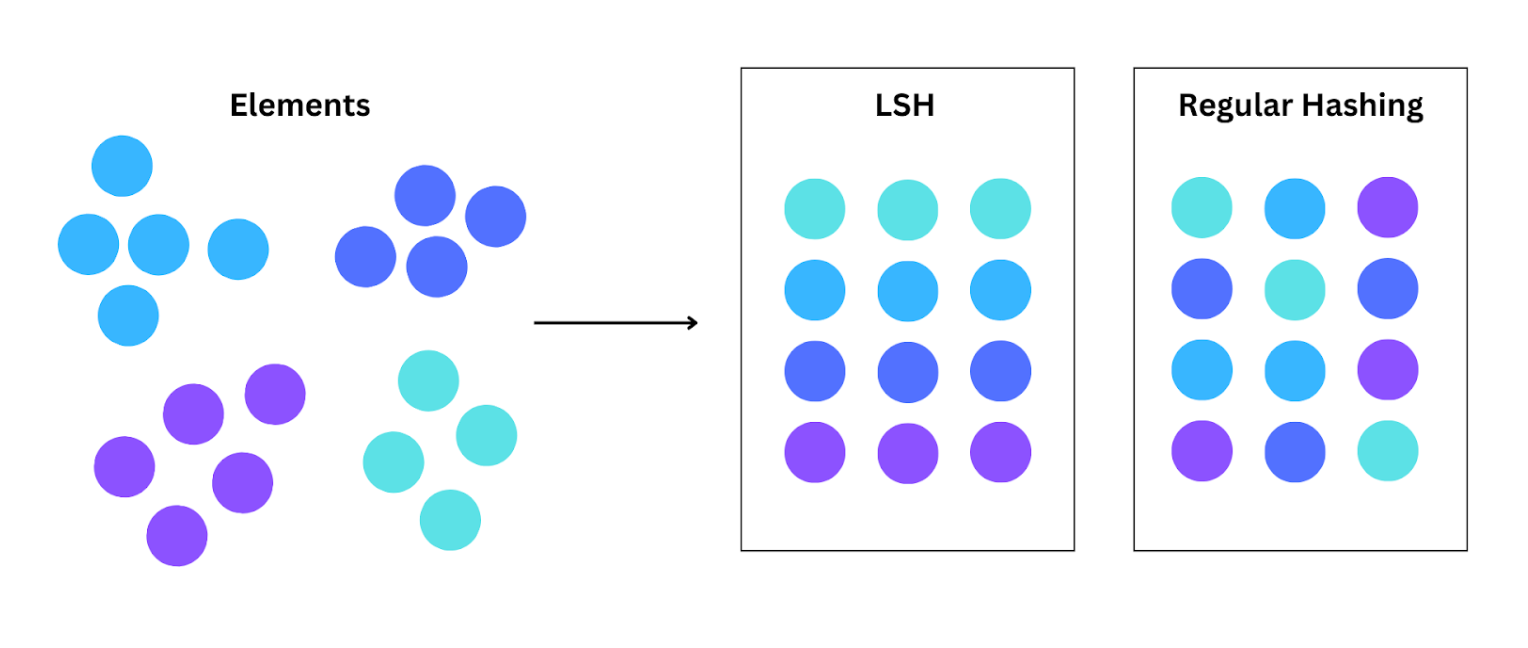LSH vs Regular Hashing

As LSH groups similar data types across datasets using multiple hash functions, the similarity search is narrowed down quickly. It does this by focusing on potentially relevant data points closer together in the high-dimensional space, speeding up the searches. Random hash functions play a crucial role in ensuring consistent performance across various datasets. Randomly chosen hash functions improve performance by applying probabilistic guarantees equally to all datasets. This approach makes it useful for applications like nearest-neighbor search for recommender systems, duplicate detection, and more.

How Does LSH Work?

Local Sensitivity Hashing operates in three major steps: Shingling, Minhashing, and Locality Sensitive Hashing. In this process, data points with the same hash code are grouped together in hash buckets, facilitating efficient querying by allowing similar items to be quickly located and examined based on their shared hash codes.

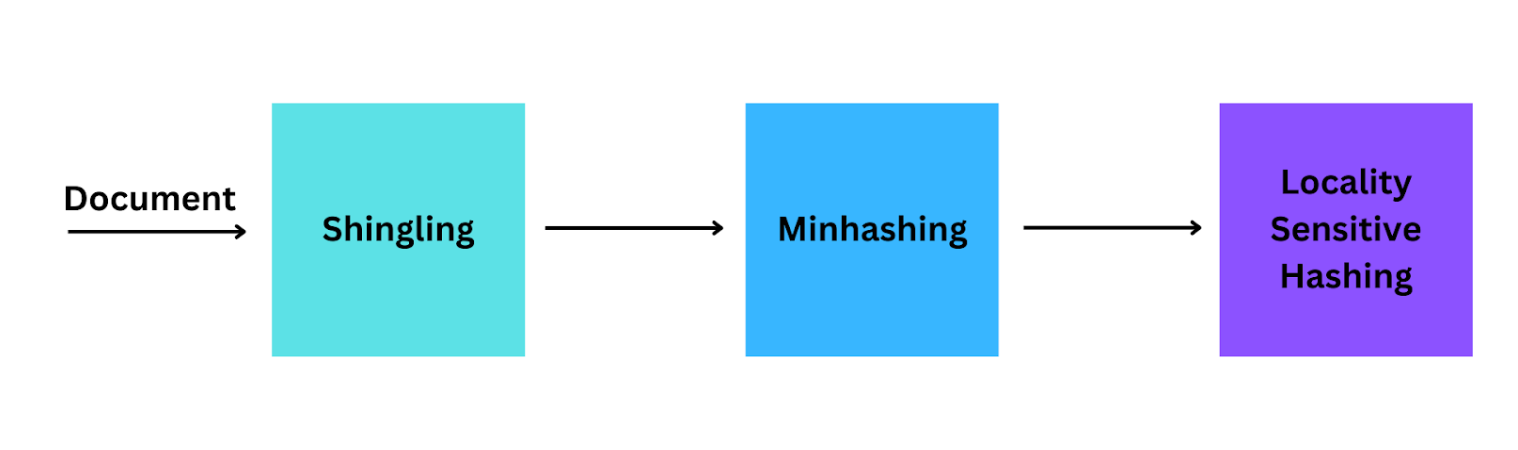The key steps of an LSH algorithm

Shingling

This step focuses on converting the documents into a set of characters of length k (also known as k-shingles or k-grams). This conversion allows you to represent the documents to be compared based on set similarity metrics, such as Jaccard similarity.

Minhashing

This technique studies the similarity between two data sets by assigning Minhash signatures and comparing them. Signatures are used to compare these sets because they capture the essence of the document’s content in a shorter form. This is the step where the Jaccard index is used. The Jaccard index of two sets is the number of common elements divided by the length of all the elements.

LSH technique

This step includes clustering similar items together. Random projections are a technique used to reduce the dimensionality of a set of points. The LSH technique uses multiple random projection functions to map the document signatures into a lower-dimensional space. This wraps up the process because the random projections are designed so that similar documents and signatures will likely be mapped into the same bucket. Similar documents are likely to be mapped to the same hash value, facilitating efficient querying.

Implementing LSH

To implement LSH, you can use a few steps we have included in the following code snippets.

Using a single hash function in high-dimensional spaces can lead to less flexible results and poorer performance in identifying approximate neighbors. Instead, utilizing multiple hash functions can improve lookup accuracy for similar items.

Start by including the following libraries.

import numpy as np

Once you’re done with that, you can define the hash function.

def hash_function(datapoint, random_vector):
  """
  Hashes a datapoint using a random projection vector.


  Args:
      datapoint: A NumPy array representing the datapoint.
      random_vector: A NumPy array representing the random projection vector.


  Returns:
      A single-bit hash value (0 or 1).
  """
  projection = np.dot(datapoint, random_vector)
  return 1 if projection >= 0 else 0

This function takes a datapoint and a random projection vector as input. It calculates the dot product between them, and if the projection is non-negative, it returns 1. Otherwise, it returns 0. This process creates a single-bit hash value depending on the relationship between the data point and the random vector.

Generate a random projection matrix.

def generate_random_matrix(num_projections, data_dim):
/*
  Generates a random projection matrix with specified dimensions.


  Args:
      num_projections: Number of random projection vectors to generate.
      data_dim: Dimensionality of the datapoints.


  Returns:
      A NumPy array representing the random projection matrix.
*/
  return np.random.randn(num_projections, data_dim)

More specifically, let’s discuss the role of this function. The num_projections is an integer that details how many random projection vectors you’d want to create, while the data_dim is another integer that shows the dimensionality of your data points.

Overall, this function generates a matrix where each row is a random projection vector you can use later on to project your high dimensional data points into a lower dimensional space, preparing it for the next function, Local Sensitive Hashing.

Start to operate local sensitive hashing.

def lsh_hash(datapoint, random_matrix):
  """
  Hashes a datapoint using multiple random projections.


  Args:
      datapoint: A NumPy array representing the datapoint.
      random_matrix: A NumPy array representing the random projection matrix.


  Returns:
      A list of hash values (one for each random projection vector).
  """
  hash_values = []
  for random_vector in random_matrix:
    hash_values.append(hash_function(datapoint, random_vector))
  return hash_values

The ish_hash function hashes a data point using multiple random projections, a core step in the LSH process. The first line includes the NumPy arrays datapoint and random_matrix, which represent the datapoint to be hashed and the random projection matrix for hashing, respectively.

Moving on to the process steps, the initialization step is executed by hash_values, which creates an empty list to store the generated hash values.

This is followed by the iteration process, which is done through random projection vectors. The random_matrix loops through each row, and then the random_vector calls the hash_function with the datapoint and random_vector as arguments.

Then you’ll get the return values in the hash_values list, containing a hash value for each random projection vector.

# Sample datapoint
datapoint = np.array([1, 2, 3])


# Number of random projections
num_projections = 2


# Dimensionality of datapoints
data_dim = len(datapoint)


# Generate random projection matrix
random_matrix = generate_random_matrix(num_projections, data_dim)


# Hash the datapoint
hash_values = lsh_hash(datapoint, random_matrix)


# Print the hash values
print("LSH Hash:", hash_values)

This code snippet generates a sample data point. It defines the number of random projections and data dimensionality, generates a random projection matrix, hashes the data point, and prints the hash values in 1s and 0s.

LSH Applications and Use Cases

LSH was designed to effectively and efficiently conduct similarity searches, which gives them a range of applications in various fields. One of its most applied use cases is in computational biology, specifically in gene and protein sequence analysis. This is because LSH can help identify similar gene expressions in genome databases, especially since gene expression data often has high dimensions.

Another widely used application of LSH is image retrieval. the LSH function maps out high-dimensional image data to lower representations while maintaining the similarity between data. This facilitates fast retrieval of images similar to a query image. This applies to stock photo services, where users request certain visuals, medical image analysis, where finding a similar case could help with diagnosis, and more. It has also improved hashing techniques and compression performance in image retrieval applications. LSH is also used in plagiarism detection software. It helps identify the similarity between documents, often with a percentage and highlighting the similar areas. LSH has other applications, such as video retrieval, social network analysis, recommendation systems, and data mining, all owing to its ability to spot similarities between datasets.

Summary of locality sensitive hashing

Local Sensitivity Hashing (LSH) is a pivotal technique for tackling the complexities of large, high-dimensional datasets, streamlining the process of similarity search and data retrieval. Its capacity to efficiently map similar data points to the same 'buckets' in a reduced-dimensional search space, makes it an invaluable tool in various sectors. From powering recommendation systems in e-commerce to facilitating advanced research in computational biology, LSH's role in enhancing search efficiency and accuracy is undeniable.

Shanika W.

Next: Optimizing AI: A Guide to Stable Diffusion and Efficient Caching Strategies