Learn
AI & Machine Learning

The Evolution of Multi-Agent Systems: From Early Neural Networks to Modern Distributed Learning (Algorithmic)

Oct 13, 202413 min read

In this article, we'll discuss the evolution of MAS from its early days to the most recent developments from an algorithmic perspective.

By Ruben Winastwan

Read the entire series

This is the first article in a two-part series. Check out the second article here.

The evolution of Multi-Agent Systems (MAS) has come a long way. Before the inception of MAS, systems typically worked in isolation to solve particular tasks. For example, an object detection model would detect all possible objects in an image. If we needed it to detect more granular objects, we would fine-tune the same model on smaller, more relevant datasets. The idea was to use a single model to solve a task.

However, what if we had several object detection models, each specializing in detecting particular objects? Together, they could collaborate to solve challenging object detection tasks and achieve better results than using a single model for all object detection tasks. This system, where several models collaborate to solve a task, is a practical implementation of MAS.

In this article, we'll discuss the evolution of MAS from its early days to the most recent developments from an algorithmic perspective. So, without further ado, let's start with one of the earliest methods: the SMFFNN framework.

SMFFNN Framework

Neural networks have proven highly reliable when predicting test data similar to their training data. However, they struggle when the test data deviates significantly from the training data.

For example, let's say we have trained a neural network to classify dog and cat pictures using a large dataset of cat and dog images. If our test data contains a picture of a cat, our model will likely give us a good result. However, if our data contains a picture of a giraffe, our model will give us an incorrect prediction. In other words, neural networks often struggle to deal with the complexity of real-world data that falls outside their training distribution.

One of the earliest methods to address this drawback of neural networks is the combination of a Supervised Multi-layer Feed-Forward Neural Network (SMFFNN) and potential weights linear analysis (PWLA).

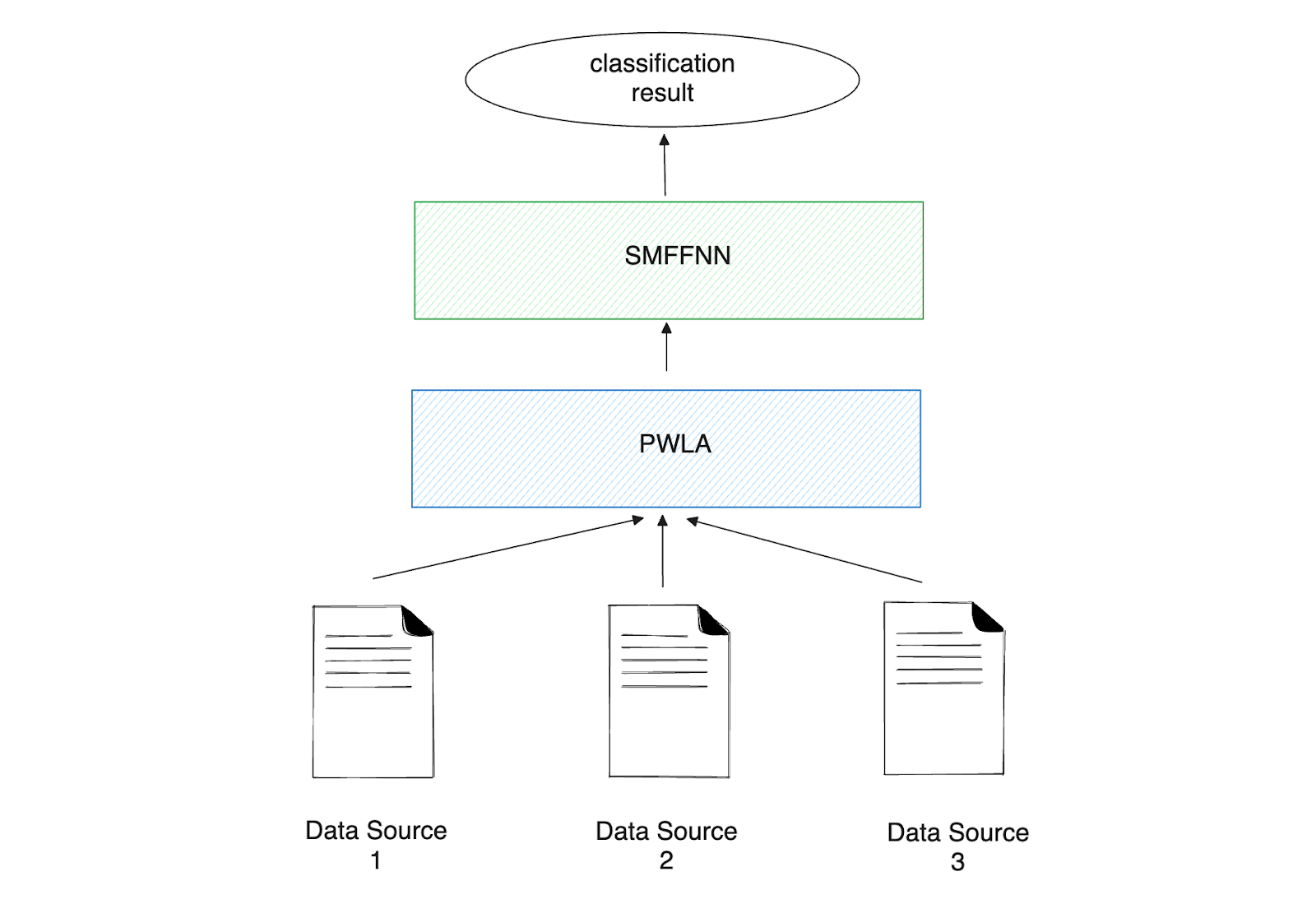Figure- Workflow of PWLA and SMFFNN..png

Figure: Workflow of PWLA and SMFFNN.

As the name suggests, SMFFNN consists of a multi-layer neural network. It's trained for only one epoch using a binary step function that simplifies the decision-making of each layer to a clear "yes" or "no," making the network much faster to train. Before the training process of SMFFNN, the data must be preprocessed by PWLA.

In a nutshell, PWLA is a data preprocessing technique that can make an initial guess about which parts of the data are important using concepts from physics, such as vector torques. It first normalizes the input data using a "min and max" method, determines which parts of the data are important, and then performs dimensionality reduction by focusing on the most relevant aspects of the data.

The processed data is then used by SMFFNN for training and making accurate predictions. The advantage of this approach is that when new data becomes available, we can integrate it directly into PWLA. We can see an early application of MAS here, as PWLA and SMFFNN work together to classify data from different sources.

For example, let's say we want a MAS to classify which city needs a hospital the most. To do this, we'd first collect population, distance from the capital, number of local staff, number of people with medical insurance, number of existing hospitals, etc. Next, PWLA gathers all this data, performs data normalization, analyzes which features are important for our use case, and then performs dimensionality reduction to focus on the most important features. Finally, we send these features to SMFFNN for training and prediction.

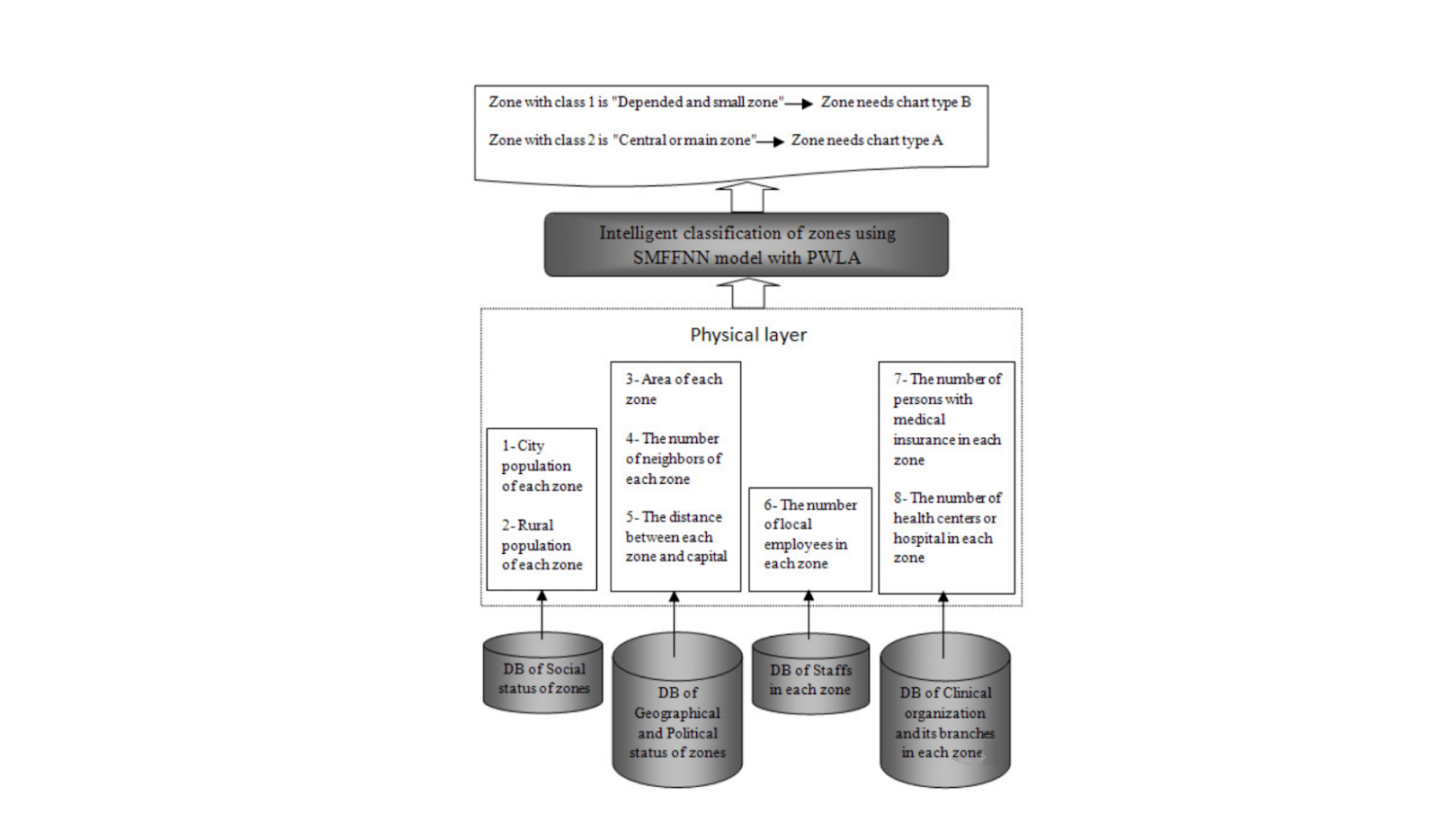Figure- Example Use Case Illustration- Intelligent classification of zones for building a hospital.

Figure: Example Use Case Illustration: Intelligent classification of zones for building a hospital. | Source.

However, this method comes with several limitations.

By design, SMFFNN and PWLA follow a unidirectional flow of information and thus struggle with the concept of feedback mechanisms required to build an intelligent multi-agent system. In a real-world multi-agent system, agents must be capable of evolving their behaviors based on feedback or new data. However, the SMFFNN system lacks a feedback mechanism allowing an agent to learn and adapt over time.

This system also allows single-agent interaction only. If we add more SMFFNNs (or agents) to the system, each agent acts more autonomously rather than being capable of efficiently sharing knowledge or adapting based on interactions with other agents. As the number of agents grows, this method might struggle to scale efficiently due to the computational complexity of training multilayer networks and performing preprocessing across all agents.

The Emergence of Reinforcement Learning

The concept behind reinforcement learning (RL) has attracted significant attention since its introduction due to its ability to be implemented without defining the dynamics of the task we want to solve, unlike supervised methods in SMFFNN. Additionally, RL introduces the concept of a feedback mechanism lacking in SMFFNN.

At a high level, an RL system consists of an agent interacting with an environment to fulfill a task. For every action an agent takes, it receives a certain amount of reward. The more aligned the agent's action is with reaching the task goal, the higher the reward it will get. Therefore, the goal of an RL system is to guide the agent in improving its future actions (policy) to maximize rewards.

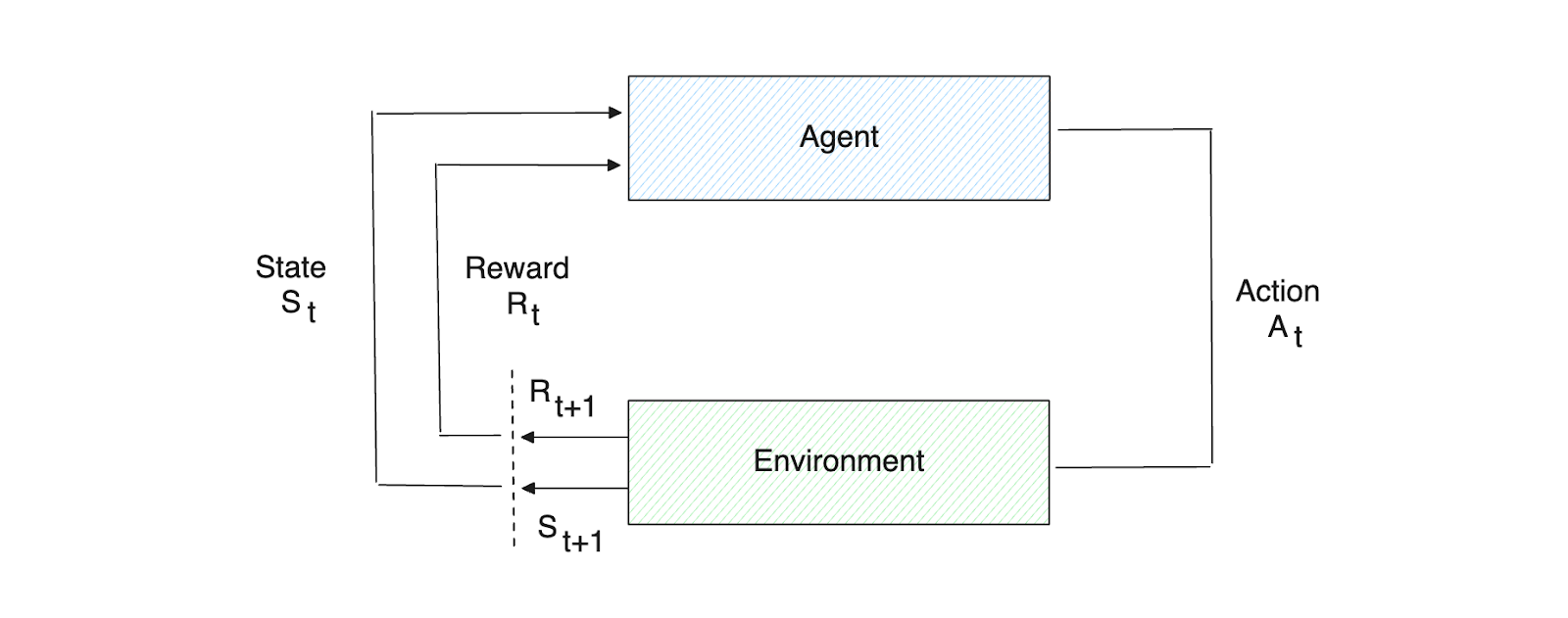Figure- Agent-Environment interaction per iteration in an RL system.

Figure: Agent-Environment interaction per iteration in an RL system.

To maximize rewards, a metric called Q-value is introduced. Q-values evaluate how good it is for an agent to take a particular action in a given state based on the future rewards it expects to receive. The agent uses this information to decide which actions to take to maximize its long-term cumulative reward.

Deep Q-learning (DQN) and Deep Deterministic Policy Gradient (DDPG) are two of the best-known RL algorithms for maximizing an agent's Q-values.

DQN focuses entirely on optimizing the Q-value function for discrete actions (such as moving right, left, forward, or backward). The Q-value is updated in each iteration using the Bellman equation based on the reward it receives from the environment and the future expected rewards, leading to the optimal Q-values and, therefore, the optimal policy.

Meanwhile, DDPG is an algorithm that consists of two components:

Actor: The actor's role is to directly output the best action for each state.
Critic: The critic estimates the Q-value, similar to how Q-values are learned in Q-Learning. However, the critic in DDPG evaluates the quality of the actions the actor selects in continuous action spaces (such as controlling a car with continuous steering angles and speed values).

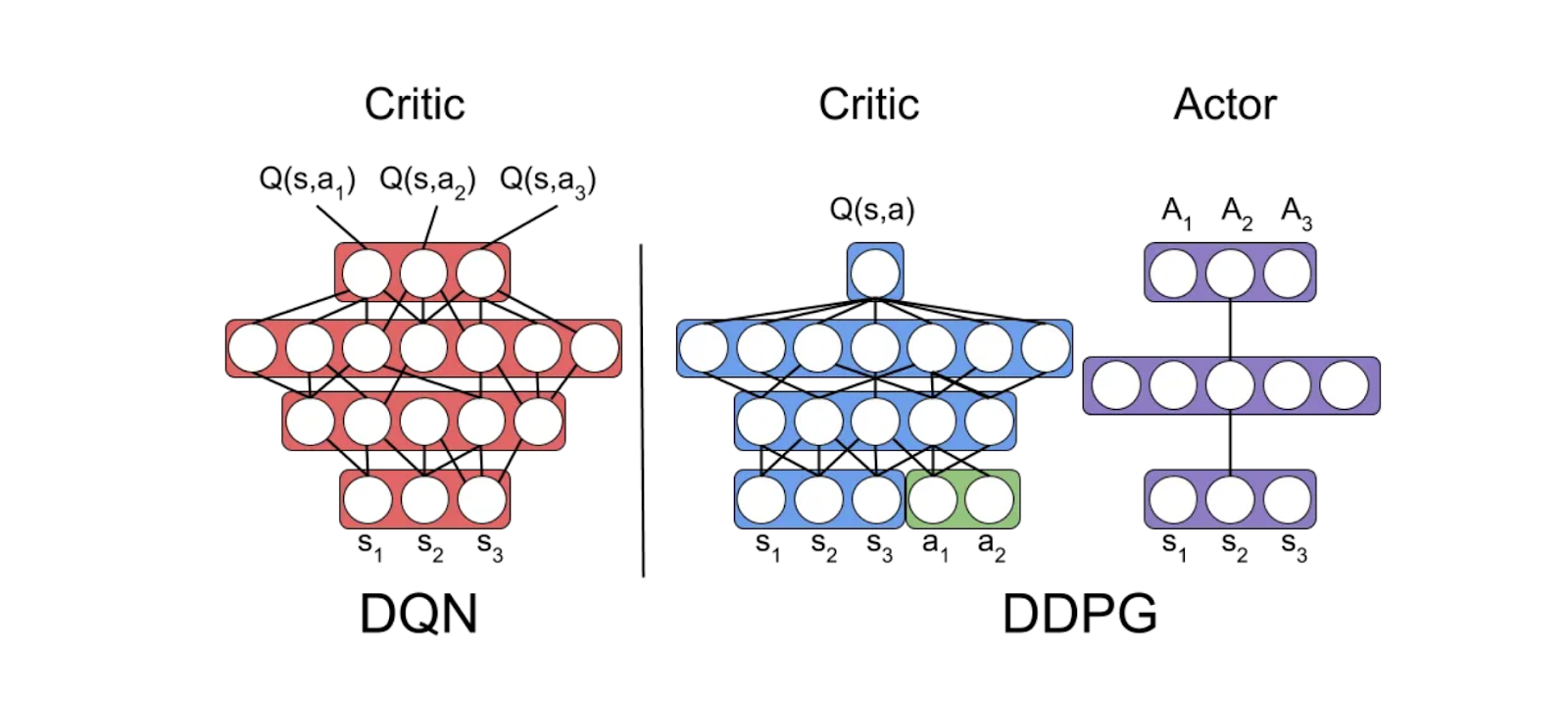Figure- Diagram of DQN and DDPG.

Figure: Diagram of DQN and DDPG. Source.

The goal of DDPG is to optimize both the actor (policy) and critic (Q-value function). Still, the critic's Q-value function plays a key role in evaluating and improving the actor's policy.

However, similar to SMFFNN, both DQN and DDPG are still designed for single-agent interaction. This means that we only optimize the policy of a single agent. One straightforward solution is to create several single agents. Unfortunately, implementing multiple RL single agents is difficult to optimize. This is because the environment is no longer stationary from each agent's perspective, and the action taken by one agent might lead to different rewards depending on the actions of other agents.

A method called Multi-Agent Deep Deterministic Policy Gradient (MADDPG) was introduced as a solution for the optimization difficulty of multiple single agents, as it can more effectively handle non-stationarity.

The key feature of MADDPG is its centralized critic, which means that the critic has access to the observations and actions of all agents during training. Therefore, the Q-value function is optimized by conditioning each agent's policy on other agents' policies. This approach is useful because it forces each agent to learn the best response to the current strategies of others rather than treating them as part of a static environment.

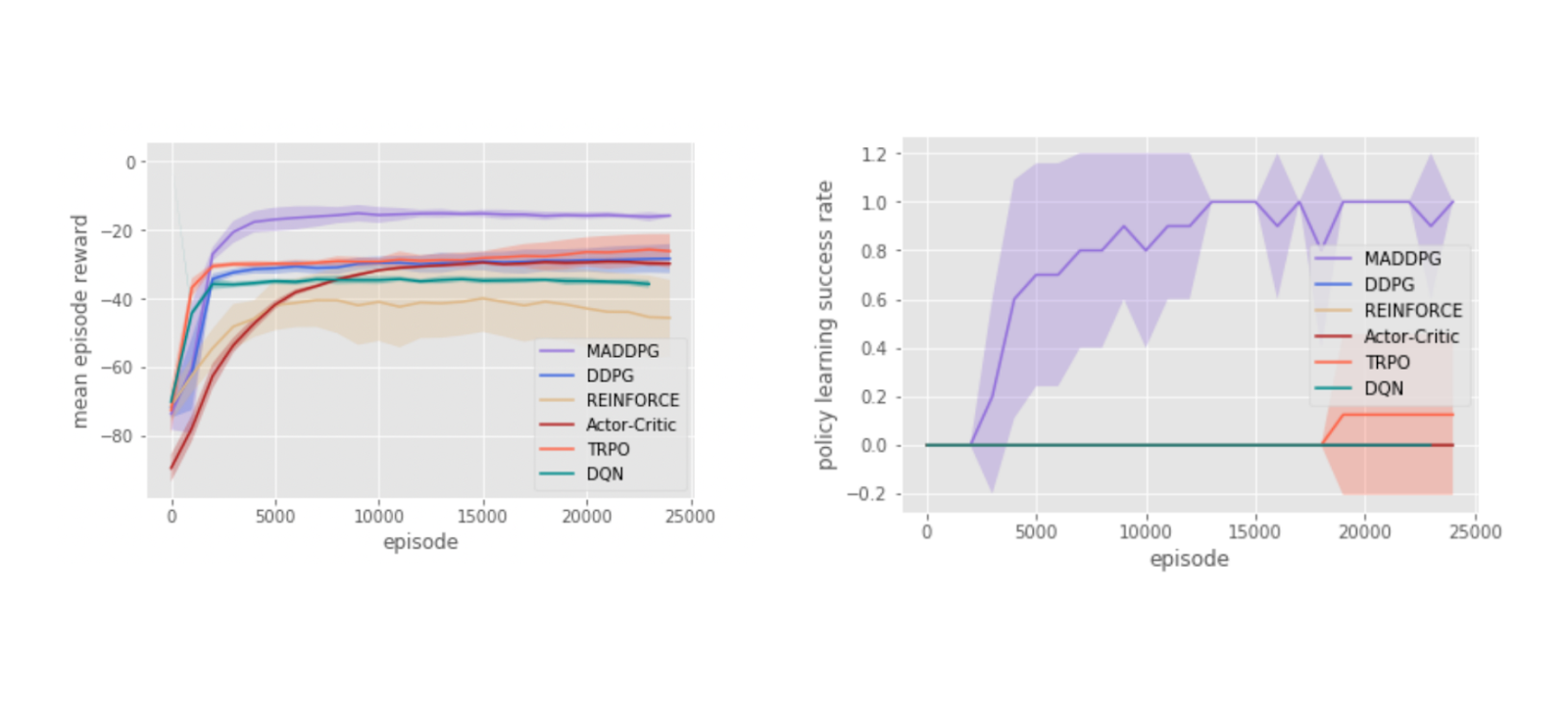Figure- Agent reward (left) and policy learning success rate (right) on cooperative communication after 25000 episodes.

Figure: Agent reward (left) and policy learning success rate (right) on cooperative communication after 25000 episodes. Source.

As you can see in the figures above, agents' performance under MADDPG is superior to that of other single-agent algorithms like DDPG in terms of agents' rewards and policy learning success rate over several episodes of experiments.

However, there is one problem regarding the MADDPG approach: the scalability issue. As mentioned above, in a centralized critic approach, the observations and actions of all agents are taken into account. As we want to train more agents, the scalability issue might become problematic, and the training process would be time-consuming and computationally expensive.

One solution that appears to address this challenge is a Graph Neural Network (GNN).

Graph Neural Network in MAS

Understanding graphs is crucial before we explore how GNNs can be used in a multi-agent system. A graph is a data structure with two fundamental elements: nodes and edges. Nodes can represent various entities, depending on the use case, such as words, agents, tokens, etc. Meanwhile, edges represent the connections between two nodes.

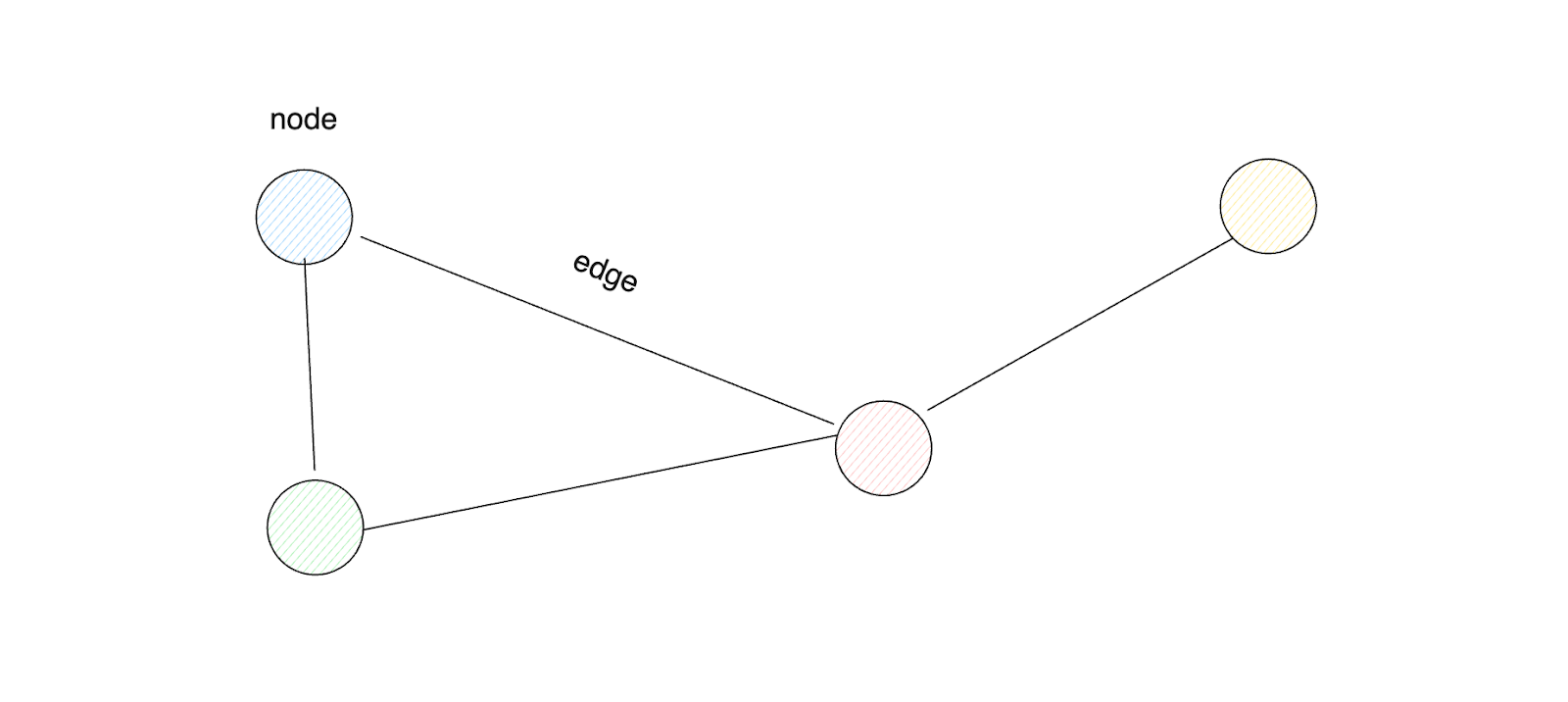Figure- Graph data structure.

Figure: Graph data structure.

Each node usually has its own features or attributes, typically represented as a vector with a particular dimension. Edges can also have features, although this is less common than for nodes. To determine which two nodes are connected by an edge, the graph structure is represented as an adjacency matrix, where A[i,j] would be 1 if there's a connection between node i and j, or 0 otherwise.

Once we have nodes, node features, and an adjacency matrix, we can implement a graph-based neural network (GNN). The goal of GNN training can be set at the node, edge, or even graph level. This means we can, for example, perform node, edge, or graph classification.

From the concepts mentioned above, we now understand that it's possible to model a multi-agent environment as a graph. This is also implemented under the hood by the method called Graph Convolutional Reinforcement Learning, or DGN for short.

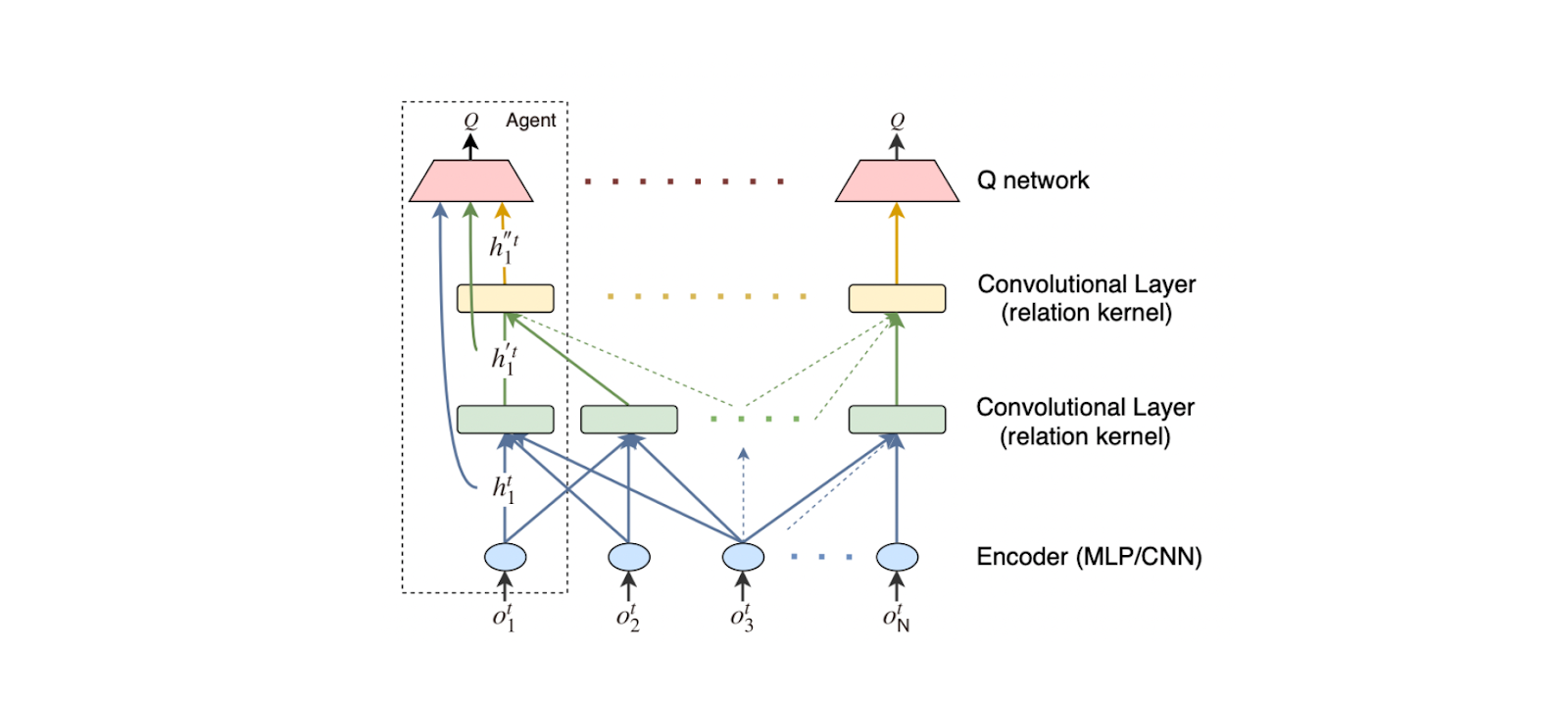Figure- DGN architectures- encoder, convolutional layer, and Q network. All agents share weights and gradients are accumulated to update the weights.

Figure: DGN architectures: encoder, convolutional layer, and Q network. All agents share weights and gradients are accumulated to update the weights. Source.

In DGN, each agent in the environment is represented by a node in the graph. Edges are formed between neighboring agents, where neighbors are typically determined by distance or other metrics, depending on the specific environment. Neighboring agents can communicate because nearby agents are more likely to interact and affect each other. The graph structure is not static but changes over time as agents move or enter/leave the environment.

DGN is easy to scale due to its parameter-sharing feature, as it shares weights among all agents. This means that all agents use the same neural network parameters, which reduces the number of parameters that need to be learned regardless of the number of agents. Also, as mentioned previously, the idea behind DGN is that nearby agents are more likely to interact and affect each other. Therefore, each agent only requires the features from its neighbors, regardless of the total number of agents in the environment.

To demonstrate its scalability feature, DGN can generalize well to scenarios with more agents than it was trained on. For example, in a routing experiment, DGN trained with 20 agents and 20 routers could perform well in settings with up to 140 agents without retraining. With DGN, we can scale the number of agents to a large number without significant degradation in performance.

Transformers in MAS

Aside from graphs, the famous Transformer architecture has also been applied to multi-agent scenarios. As you might already know, the Transformer architecture consists of an encoder and a decoder. The encoder maps the input sequence to a latent space, while the decoder generates the output in an autoregressive or sequential manner.

What makes the Transformer architecture special is an attention layer in each encoder and decoder block. This layer is crucial in providing contextual information regarding the input sequence. For example, the word 'park' in "I park my car in the garage" and "I walk outside in a park" would be perceived differently by the Transformer due to this attention layer.

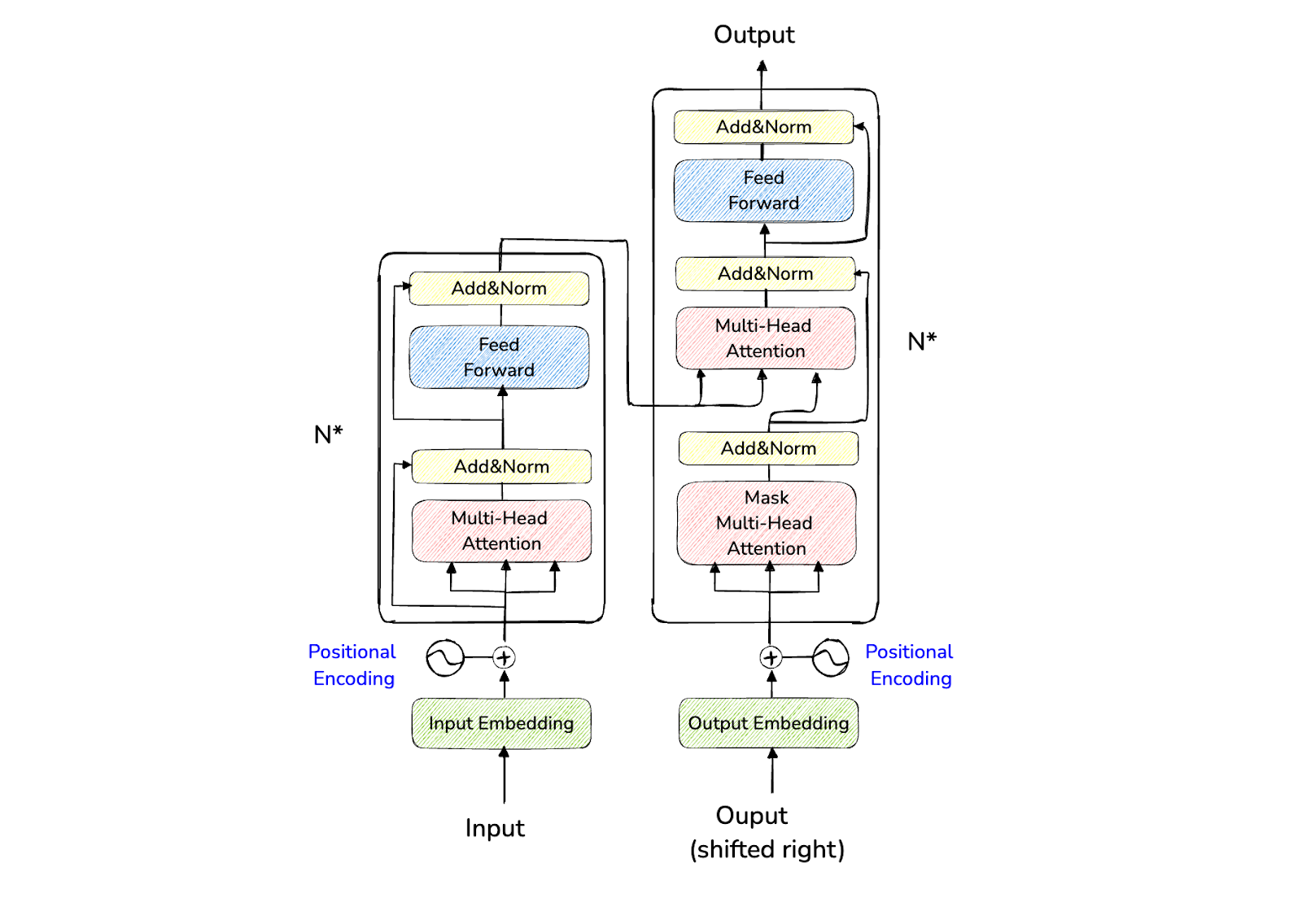Figure- Transformers architecture..png

Figure: Transformers architecture.

The Transformer architecture was originally intended only for textual use cases, such as text classification, named entity recognition, text generation, question answering, etc. However, it turns out that Transformers are versatile and can be used for different modalities, such as images, sound, etc. Therefore, it's no surprise that we can use Transformers in many use cases, including multi-agent systems.

As mentioned in previous sections, in a multi-agent system, several agents need to work together to maximize a shared reward. The challenge comes from finding optimal policies for each agent while considering how their actions interact with those of other agents. We know that non-stationarity is one of the big challenges in a multi-agent system.

One perspective on multi-agent systems is the idea that multi-agent decision-making can be thought of as a sequence of actions. This is similar to how words in a sentence are arranged in language tasks like translation. This opens the door to using sequence models (SMs) like Transformers.

One algorithm that implements Transformers in a multi-agent environment is called Multi-Agent Transformers (MAT). MAT treats the decision-making process of agents as a sequence, similar to how words in a sentence follow each other.

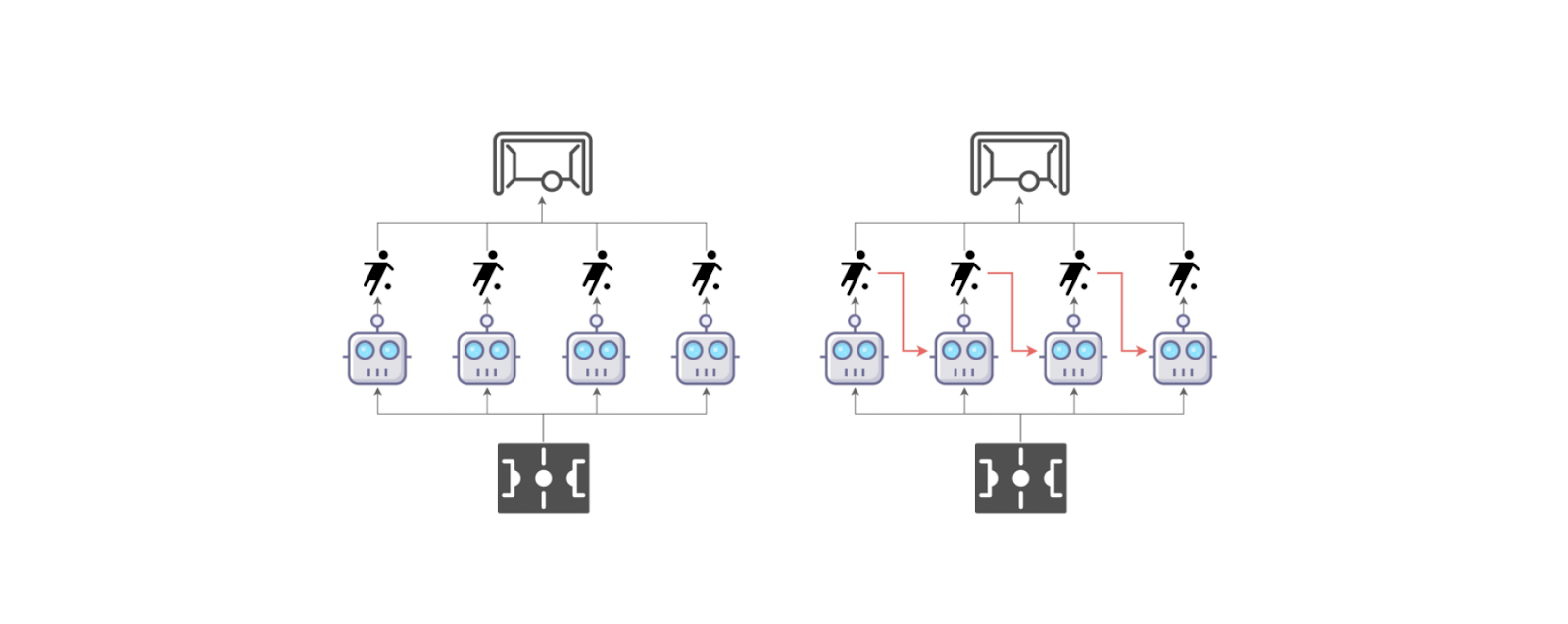Figure- Conventional multi-agent learning paradigm (left) wherein all agents take actions simultaneously vs. the multi-agent sequential decision paradigm (right) where agents take actions by following a sequential order.

Figure: Conventional multi-agent learning paradigm (left) wherein all agents take actions simultaneously vs. the multi-agent sequential decision paradigm (right) where agents take actions by following a sequential order. Source.

In the MAT approach, each agent makes a decision sequentially, like how each word is added to a sentence. This means the first agent decides its action based on what it observes. Then, the next agent sees what the first agent did, considers its observation, and decides. This process continues, with each agent considering what previous agents have done before making its own decision. By doing this, MAT reduces the complexity of agents making decisions together. It turns the problem into a step-by-step process that's easier to handle.

As MAT uses a Transformer model, it relies on an encoder and decoder in its multi-agent implementation:

Encoder: The encoder takes the observations from all agents (what they see in the environment) and converts them into useful information.
Decoder: The decoder takes this information and predicts the best action for each agent, one after the other while considering what previous agents did. It uses an attention mechanism similar to the usual text generation process to focus on the most important parts of the information when deciding the action.

As you can see in the visualization below, MAT performs superiorly on benchmark challenges compared to strong baselines such as MAPPO and HAPPO. MAT greatly simplifies the problem of coordinating multiple agents by breaking it down into manageable steps.

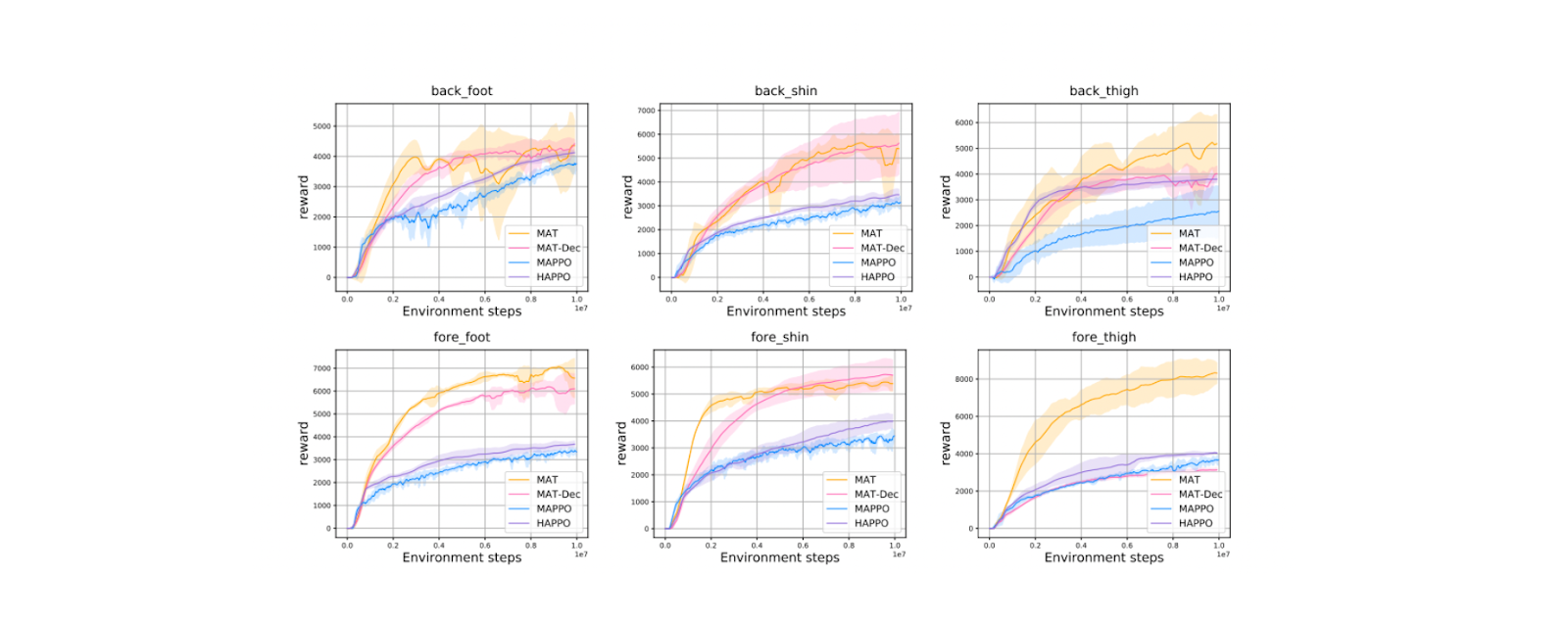Figure- Performance on the HalfCheetah task with different disabled joints. Source..png

Figure: Performance on the HalfCheetah task with different disabled joints. Source.

Conclusion

In this article, we discussed the evolution of multi-agent systems in artificial intelligence, from early neural networks to modern learning algorithms, from an algorithmic perspective. The early algorithm implementing MAS consists of a single neural network and data preprocessing technique called SMFFNN and PWLA. However, SMFFNN lacked feedback mechanisms and struggled with multi-agent interactions.

To tackle this problem, more advanced approaches were introduced, such as RL algorithms like DQN and DDPG. These RL algorithms introduced feedback mechanisms and continuous action spaces. However, the main challenge of early RL algorithms was scaling single-agent RL to multi-agent scenarios, leading to the development of MADDPG. To solve the scalability issue associated with MADDPG, Graph, and Transformer-Based algorithms can be used in MAS, and they have shown promising results compared to baseline models.

In my next article, I’ll discuss the evolution of MAS from a methodological or approach-based perspective. Stay tuned.

The Evolution of Multi-Agent Systems: From Early Neural Networks to Modern Distributed Learning (Algorithmic)

SMFFNN Framework

The Emergence of Reinforcement Learning

Graph Neural Network in MAS

Transformers in MAS

Conclusion

Further Reading

Content

Start Free, Scale Easily

Share this article