Learn
Vector Database 101: Everything You Need to Know

Mastering Locality Sensitive Hashing: A Comprehensive Tutorial and Use Cases

Apr 01, 20247 min read

Understand Locality Sensitive Hashing as an effective similarity search technique. Learn practical applications, challenges, and Python implementation of LSH.

By Haziqa Sajid

Read the entire series

As data dimensionality increases, retrieval tasks like finding the nearest neighbors become challenging. This is because the increasing distance between data points causes the curse of dimensionality, distance concentration, and the empty space phenomenon. Consequently, distance calculations and similarity comparisons become exhaustive tasks.

Locality-sensitive hashing (LSH) is a game-changer for addressing the challenges of high-dimensional data retrieval when conducting a semantic similarity search. It works by mapping similar items together with hash values while preserving local distances between the data, reducing the search space for efficient data retrieval.

LSH plays a significant role in big data in science and machine learning (ML), combating the “curse of dimensionality” and enabling practical information retrieval. By clustering similar data together, LSH allows efficient nearest neighbor search, data clustering, and other tasks requiring similarity search in large datasets.

Understanding LSH

A vector-to-vector comparison has a linear time complexity of O(n), n being the size of the search space. Comparing each vector against every other raises the complexity exponentially to O(n^2).

LSH aims to reduce this search complexity by reducing the search space. It uses a high-dimensional Euclidean space where all the data points reside and groups similar data points into the same bucket.

This is achieved by hashing similar data points within a certain distance threshold into the same bucket. Greater distance means a full hash table and higher probability of a distinct hash and vice versa. Additionally, LSH creates multiple buckets for each data point, each formed using a different hash functions. This adds robustness and improves search relevance.

Key Principles of LSH

The LSH algorithm involves two key steps. These include:

Creating multiple hash functions to generate a hash code for each data point.
Assigning data points with the same hash codes to the same hash buckets.

bucket hashing.png

Known as bucket hashing, this process defines the key principles of LSH:

Locality Locality is the core principle of LSH, which refers to mapping similar data points into the same buckets. This property guarantees approximate similarity search and clustering in high-dimensional data.
Sensitivity Sensitivity refers to dissimilar points mapped into different buckets based on their distance after hashing. This ensures that dissimilar data points are filtered out during a similarity search.
Approximate Results LSH offers approximate search, meaning dissimilar points can end up in the same bucket and similar points in different buckets. The likelihood of these errors depends upon the hash functions design and the number of hash tables. However, reducing search space and scalability outweighs the potential for errors.

Exploring LSH Algorithms and Implementation

Various LSH algorithms can be used to address the challenges of high-dimensional information retrieval.

Minhash LSH

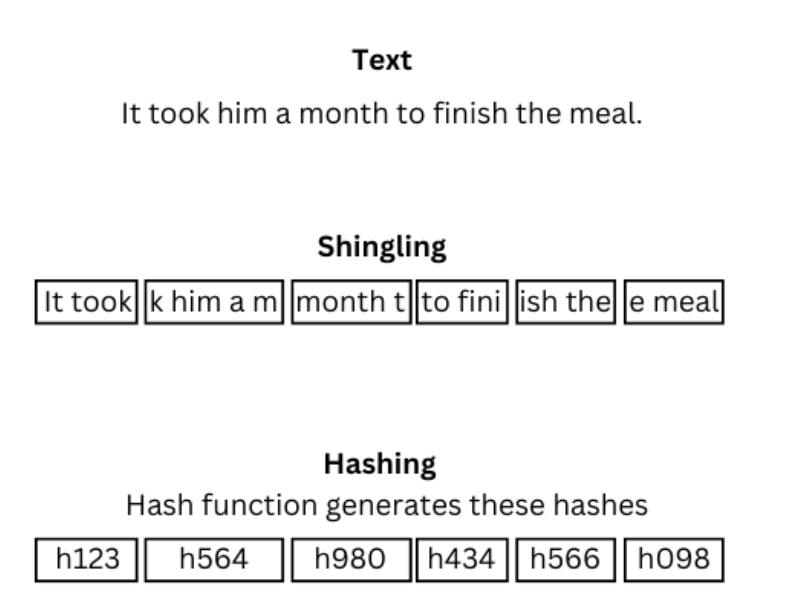
Minhash is an LSH algorithm suitable for high-dimensional documents or sets. Minhash uses the shingling method, which refers to creating overlapping fragments of a set. A set of random hash functions then takes a set of shingles and maps them to a single hash function or value.

This ensures that similar documents fall into similar hash buckets. The search query is hashed during the search, and its minhashed signature is compared with minhashes of documents in similar buckets.

The following code demonstrates a basic implementation of LSH in Python:

from collections import defaultdict

# Function to perform shingling and create MinHash signatures
def minhash(data, num_perm):
    minhash_signatures = defaultdict(list)
    
    # Create a list of hash functions
    hash_functions = [lambda x, i=i: hash(str(x) + str(i)) for i in range(num_perm)]
    
    for element in data:
        # For each element, compute the minimum hash value for each hash function
        for hash_function in hash_functions:
            minhash_signatures[element].append(min(hash_function(x) for x in element.split()))
    
    return minhash_signatures

# Function to create an LSH index, assign items to buckets, and perform a similarity search
def lsh(data, num_perm):
    # Create MinHash signatures for each data point
    minhash_dict = minhash(data, num_perm)
    index = defaultdict(list)
    
    # Assign data points to buckets based on their MinHash signature
    for point, signature in minhash_dict.items():
        bucket_id = tuple(signature)
        index[bucket_id].append(point)
    
    # Perform similarity search by finding data points in the same bucket
    similar_items = {}
    for query, query_signature in minhash_dict.items():
        bucket_id = tuple(query_signature)
        candidates = index[bucket_id]
        similar_items[query] = candidates
    
    return similar_items

# Example dataset
data = ["cat dog rabbit", "dog lizard bird", "cat bear crow", "lion lizard panda"]

# Adjust number of permutations as required
num_perm = 16

# Find similar items
similar_items = lsh(data, num_perm)

# Display the similar items
print("Similar items:")
for query, items in similar_items.items():
    print(f"\tQuery: {query}")
    print(f"\tItems: {items}")

Locality Sensitive Hashing for Jaccard Similarity

Locality-sensitive hashing for Jaccard Similarity is ideal for sets or binary vectors. It identifies similar documents or sets based on their Jaccard Similarity. The idea is to define a set of random hyperplanes, and documents on the same side of the same hash value the hyperplane are assigned similar buckets. Jaccard similarity among the documents is calculated to ensure accuracy, and documents with similar Jaccard scores land into similar buckets.

During a search, the search query is projected onto the same hyperplanes used for bucketing and data points that landed in the same hyperplane as the query are retrieved for further evaluation. This means that documents in the buckets that landed on the query point the same side of the hyperplane are retrieved for further evaluation.

datasketch library in Python offers a straightforward syntax for LSH implementation. Here’s a code that implements the LSH function for Jaccard Similarity in Python:

from datasketch import MinHash
from datasketch import MinHashLSH

# Create an LSH index with 128 permutations
minhash = MinHash(num_perm=128)

# Specify the threshold of Jaccard Similarity
lsh_jaccard = MinHashLSH(threshold=0.5, num_perm=128)

# Break "item1" into shingles and calculate minhash
minhash.update("item1".encode('utf8'))

# Assign "item1" to relevant buckets with label "item1"
lsh_jaccard.insert("item1", minhash)

# Break "item1" into shingles and calculate minhash
minhash.update("item2".encode('utf8'))

# Assign "item2" to relevant buckets with label "item2"
lsh_jaccard.insert("item2", minhash)

# Find items with similar minhash
result = lsh_jaccard.query(minhash)
print(result)

Spherical LSH

The spherical LSH algorithm suits data points that reside on a unit sphere like geospatial data. It uses random spherical subspaces to find similar data points. Data points on the same spherical subspaces are mapped to similar buckets. Cosine similarity is calculated among data points to verify the similarities. During a search, the search query is projected onto the same spherical subspaces used for bucketing. The points that landed on the same spherical subspaces as the search query are retrieved for further similarity assessment using Cosine similarity.

lshash library in Python provides a simple syntax for Spherical LSH implementation. Here’s a code that implement it in Python:

from lshash import LSHash

# Create a 6-bit hash function for input data with 8 dimensions
lsh_hash = LSHash(6, 8)

# Apply the hash function to each data point of 8 dimensions input
lsh_hash.index([2, 3, 4, 5, 6, 7, 8, 9])
lsh_hash.index([10, 12, 99, 1, 5, 31, 2, 3])

# Query a single similar data point
num_similar_point = 1
nn = lsh_hash.query([1, 2, 3, 4, 5, 6, 7, 7], num_results=num_similar_point, distance_func="cosine")
print(nn)

Practical Applications of LSH

LSH is crucial for information retrieval from large databases. A few of its data science applications where it shines significantly improving the search speed while preserving accuracy are:

LSH is crucial for information retrieval from large databases. A few of its data science applications where it shines significantly improving the search speed while preserving accuracy search quality are:

Image Retrieval Searching relevant images from a repository of millions of images is computationally exhaustive. LSH extracts feature vectors from the images and projects them into a smaller dimensional space. Similar images have similar feature vectors, which are stored in similar hash tables. This significantly reduces the dataset size, resulting in faster retrieval.
Plagiarism Detection LSH converts text documents into sets of shingles. During the plagiarism detection, the algorithm identifies the documents with similar shingles, indicating potential plagiarism. Relevant documents are then further evaluated to verify the plagiarism. This allows for the detection of plagiarism from massive amounts of documents in less time while keeping the results accurate.
Near-Duplicate Detection Near-duplicate documents have almost similar content but aren’t identical, i.e., slightly modified product descriptions or paraphrased texts. Jaccard LSH is a suitable LSH algorithm to detect near-duplicate documents, projecting documents on a random hyperplane. Jaccard Similarity is then used to map similar documents into similar hash tables. This reduces the number of documents to be scanned during the search, resulting in faster and more efficient near-duplicate detection.

LSH’s ability to efficiently navigate large datasets for accurate information retrieval makes it an essential tool for efficient approximate neighbor search. Reducing the computational burden of similarity search while maintaining high precision, LSH extracts accurate insights from vast amounts of data.

Conclusion

I hope that you liked this locality sensitive hashing python tutorial and now have a good idea how hash functions work to make your nearest neighbor search efficient! Locality Sensitive Hashing is a powerful technique that accelerates nearest neighbor searches from large databases. It achieves this without compromising on accuracy, thanks to its robust hash functions and similarity measures. This is a key aspect that makes LSH a significant tool in your work.

With all these benefits, LSH makes dealing with high-dimensional databases easier and enhances the efficiency of AI systems. LSH is a technique with great potential for revolutionizing data retrieval methods.

Explore libraries like lshash and datasketch in Python for easier LSH implementation. While these libraries simplify your task, algorithm efficiency depends on a well-tuned configuration. Designing a well-tuned configuration takes practical knowledge and enough practice, so play around with different LSH techniques to embrace its true potential.