Learn
Accelerated Vector Search

Next-Gen Retrieval: How Cross-Encoders and Sparse Matrix Factorization Redefine k-NN Search

Dec 05, 202411 min read

AXN (Adaptive Cross-Encoder Nearest Neighbor Search) uses a sparse matrix of CE scores to approximate k-NN results, reducing computation while maintaining high accuracy.

By Haziqa Sajid

Read the entire series

Efficient k-nearest neighbor (k-NN) search is fundamental for tasks like finding similar items or retrieving relevant information. In these searches, the goal is to determine the most relevant neighbors for a given query. Cross-encoders (CEs) are highly accurate in evaluating the relevance of query-item pairs because they consider both simultaneously. However, their high computational cost makes them unsuitable for large-scale k-NN searches, where thousands or millions of comparisons are required.

Dual-encoders (DEs) are often used to address this scalability issue. DEs precompute numerical representations (or vector embeddings) of queries and items separately, making retrieval faster. However, this efficiency comes at the cost of accuracy, particularly in new or unfamiliar domains, where DEs tend to underperform without additional fine-tuning. Another approach is CUR matrix factorization, which balances accuracy and efficiency by approximating the relevance matrix (the relationship between queries and items). While it improves performance compared to DEs, it still relies heavily on multiple CE computations, making it costly and impractical for large-scale applications.

Due to the limitations of current methods, there is a need to develop a more efficient and accurate approach for approximating confidence estimates in k-nearest neighbor (k-NN) search. The objective is to create a method that:

Requires significantly fewer CE calls for indexing items than CUR-based methods.
Achieves higher accuracy than DE-based retrieve-and-rerank methods, especially in new domains, without necessitating additional fine-tuning of the DE.

AXN (Adaptive Cross-Encoder Nearest Neighbor Search) introduces a novel solution to meet this need. It uses a sparse matrix of CE scores to efficiently approximate k-NN results, significantly reducing computation while maintaining high accuracy. If you're interested in exploring the details of these methods, check out the research paper for an in-depth understanding.

Understanding Key Concepts: Laying the Foundation

Before delving into the innovative methodologies discussed in this blog, it is important to grasp the fundamental building blocks.

K-Nearest Neighbor (k-NN) Search: K-Nearest Neighbor (k-NN) search is a fundamental retrieval method in machine learning. It identifies the closest k items to a given query based on a predefined similarity metric, such as distance or relevance. This technique is a cornerstone in applications such as recommendation systems, search engines, and natural language processing (NLP) tasks, where finding relevant matches is critical.
Cross-Encoders (CE): Cross-encoders (CE) are similarity functions that take a pair of data points (e.g., a query and an item) as input and directly output a scalar similarity score. They achieve state-of-the-art results in tasks such as Question Answering (QA) and Entity Linking. However, CEs are computationally expensive, especially when parameterized using deep neural models like transformers.

Methodologies for Efficient k-NN Search with Cross-Encoders

Now, let's discuss the primary methodologies for efficient k-nearest neighbor (k-NN) search using cross-encoder models, addressing the computational challenges of deploying these expensive models for large-scale retrieval tasks. The core idea is around efficiently approximating the cross-encoder scoring function using a dot product in a learned embedding space.

The methodologies can be broadly categorized into two stages:

Offline Indexing Stage: Sparse-Matrix Factorization
Online k-NN Search Stage (AXN): Adaptive Cross-Encoder Nearest Neighbor Search

Offline Indexing with Sparse-Matrix Factorization

The standard approach to indexing items for CE-based search includes using CUR decomposition, which requires many CE calls and is impractical for large datasets. A sparse-matrix factorization-based approach addresses this limitation by constructing a sparse matrix, denoted as G, containing cross-encoder scores for a carefully selected subset of query-item pairs and then factorizing this matrix to learn item representations. The sparse nature of the matrix arises from the fact that computing cross-encoder scores for every possible query-item pair is computationally prohibitive.

There are two main variants of matrix factorization.

Transductive Matrix Factorization (MF_TRNS)
Inductive Matrix Factorization (MF_IND)

Transductive Matrix Factorization (MF_TRNS)

Transductive Matrix Factorization treats both query and item embeddings as trainable parameters and directly learns these embeddings by minimizing the difference between the observed cross-encoder scores in G and the dot product of the learned embeddings.

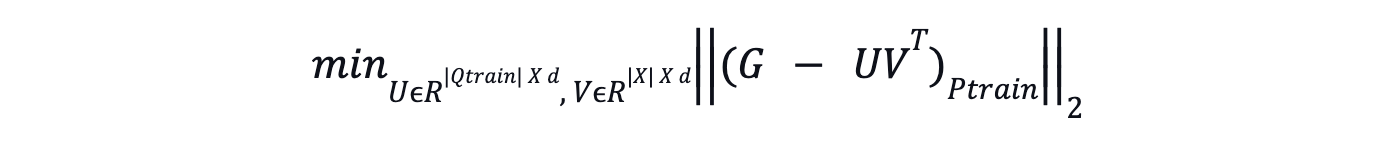equation -Transductive Matrix Factorization .png

Where:

G is the sparse matrix containing cross-encoder scores between training queries (Q_train) and a subset of items (I).
P_train denotes the projection on the set of observed entries in G.
U and V are matrices whose rows correspond to the embeddings of a query and an item, respectively.

While effective for smaller datasets, MF_TRNS can be computationally expensive and memory-intensive for large item sets due to the large number of trainable parameters.

Inductive Matrix Factorization (MF_IND)

MF_IND trains shallow MLPs to map raw query and item features to the embedding space to improve scalability. These MLPs are trained by inputting query and item embeddings from a base dual-encoder model (trained on a related task but not fine-tuned on the target domain) and producing refined embeddings that better approximate the cross-encoder scores. This approach gives better generalization to unseen queries and items and is computationally more efficient than training a full DE model via distillation.

Sparse Matrix Construction Strategies

There are two main strategies for constructing the sparse matrix for the k-NN search method with cross-encoders:

Fixed Items per Query

Given a set of training queries (Q_train ) train, this strategy selects a fixed number of items (k_d) for each query to construct the sparse matrix G. The selection of items can be done uniformly at random or by using a baseline retrieval method like a dual-encoder model (DE_SRC). This strategy works best in scenarios where queries are more diverse than items.

Fixed Queries per Item

This strategy selects a fixed number of training queries for each item in the item set (I). The selection process can again be randomized or based on a baseline retrieval method. This approach is ideal when items are more diverse than queries.

Online k-NN Search with AXN

AXN (Adaptive Cross-Encoder Nearest Neighbor Search) performs a k-NN search for a given test query by adaptively refining its embedding using feedback from cross-encoder scores. This method efficiently finds the k-nearest neighbors for a given query by adaptively refining the query embedding and using approximate CE scores for retrieval. The item embeddings remain fixed throughout this process.

AXN operates over multiple rounds, incrementally improving the approximation of the cross-encoder scores for the test query. It starts by randomly retrieving a small set of items or using a baseline retrieval method like a dual-encoder or TF-IDF. The cross-encoder then scores these items, and the initial query embedding is computed by solving a system of linear equations. In subsequent rounds, AXN retrieves additional items based on the approximate cross-encoder scores computed using the current query embedding and the fixed item embeddings. The exact cross-encoder scores for these newly selected items are computed and used to update the query embedding for the next round.

This process continues for a fixed number of rounds or until a computational budget is exhausted. The budget is distributed evenly across the rounds. Finally, the retrieved items are ranked based on their exact cross-encoder scores, and the top-k items are returned as the approximate k-NN for the given test query.

AXN - Test-time k-NN Search Inference

Below, the algorithm provides a step-by-step procedure for performing the adaptive k-NN search with AXN.

Figure- AXN Algorithm .png

Figure: AXN Algorithm | Source

Regularization of Test Query Embedding

Regularizing is used to prevent overfitting during the refinement process. This is done by combining the query embedding obtained from the adaptive refinement process with the embedding from a parametric model like a DE model using a weighted average. This regularization helps generalize unseen items and improve retrieval quality. The final test query embedding as:

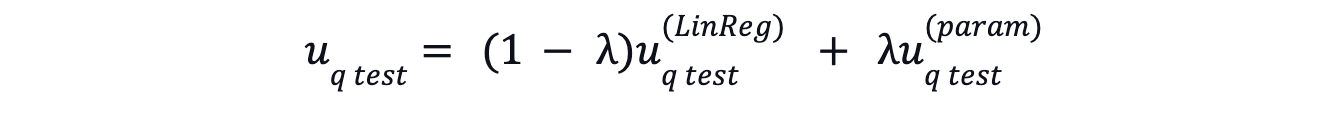equation -regularization.png

Analysis of the Results from AXN and Sparse Matrix Factorization

Two popular benchmark datasets, ZESHEL (for zero-shot entity linking) and BEIR (for zero-shot information retrieval), are used to evaluate the effectiveness of the proposed sparse-matrix factorization and AXN methodologies against various baseline approaches, including retrieve-and-rerank using different retrieval models and ADACUR, a recently proposed CUR decomposition-based method.

AXN vs. Retrieve-and-Rerank (RNR)

The adaptive k-NN search method, AXN, performs better than the traditional retrieve-and-rerank (RNR) approach. For example, on the YuGiOh dataset (test domains from ZESHEL dataset), AXN using DE_SRC for both indexing and initial retrieval achieves a 5.2% improvement in Top-1-Recall and a remarkable 54% improvement in Top-100-Recall compared to RNR with DE_SRC. Notably, this performance gain comes with minimal computational overhead.

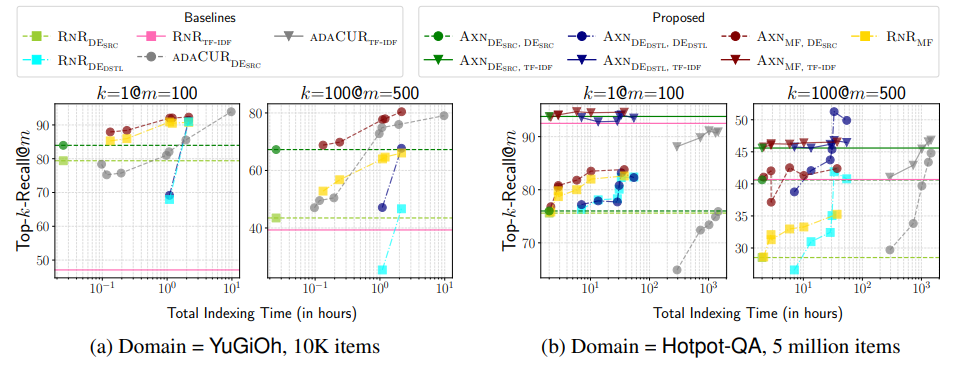Figure- Top-1-Recall and Top-100-Recall vs. indexing time for various approaches.png

Figure: Top-1-Recall and Top-100-Recall vs. indexing time for various approaches| Source

The x-axis represents the total indexing time, encompassing steps like computing embeddings and training models. The y-axis shows the Top-1-Recall@100 and Top-100-Recall@500, meaning the fraction of top-k neighbors (as per the cross-encoder) found within the top 100 and 500 retrieved items, respectively.

Matrix Factorization vs. DE_DSTL

Matrix factorization-based approaches, particularly the inductive variant (MF_IND), demonstrate a remarkable ability to balance efficiency and accuracy. They consistently match or surpass the distillation-based methods' performance for training dual-encoder models while requiring significantly less computational resources for indexing. This efficiency stems from using a sparse matrix for factorization and training a shallow MLP in MF_IND, leading to fewer parameters compared to training a full dual-encoder model.

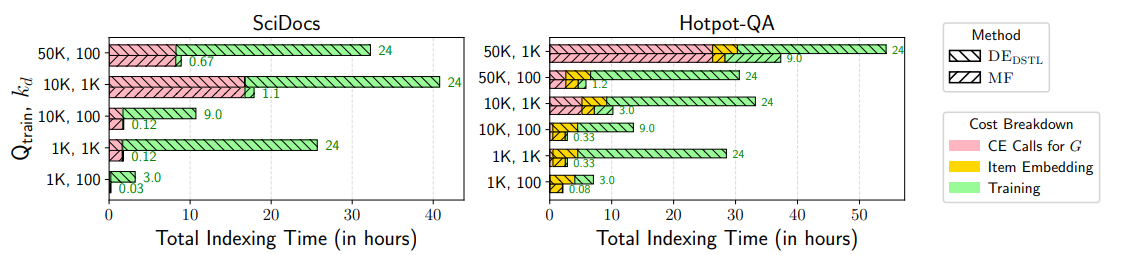Figure- Indexing latency of MF and DEDSTL.png

Figure: Indexing latency of MF and DE_DSTL| Source

Significant Indexing Speedup over ADACUR

The proposed approaches, especially when combined with AXN, show a significant advantage in indexing speed compared to the recent CUR decomposition-based method, ADACUR. For instance, on the large-scale Hotpot-QA dataset (datasets from BEIR), ADACUR requires over 1000 GPU hours to index 5 million items. In contrast, MF_IND, coupled with AXN using DE_SRC for initial retrieval, achieves comparable retrieval accuracy while completing the indexing process in under three hours. This shows the computational efficiency of the sparse-matrix factorization approach.

Downstream Task Performance Analysis

The evaluation of improved k-NN search accuracy shows varying impacts on downstream task performance across different datasets. While improvements in k-NN recall directly correlated with better downstream task performance for the Hotpot-QA dataset, the trend differs for other datasets like SciDocs, YuGiOh, and Star Trek. On these datasets, exact brute-force search with the cross-encoder leads to suboptimal downstream task performance compared to RNR_DESRC.

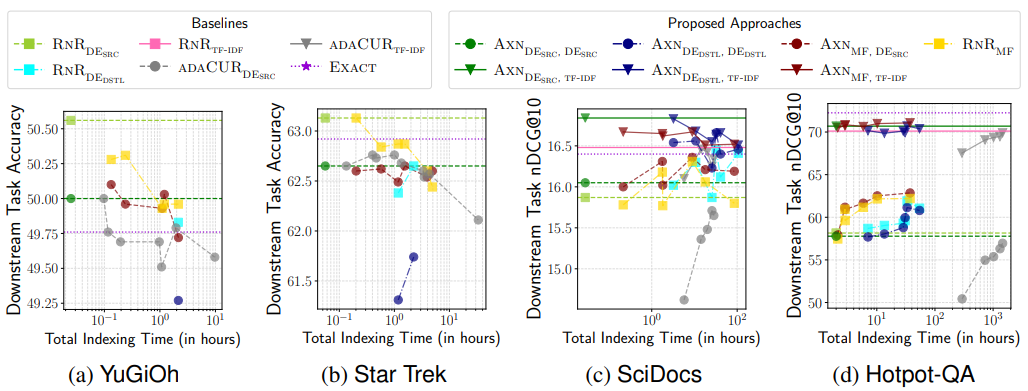Figure- Downstream task performance vs. indexing time.png

Figure: Downstream task performance vs. indexing time | Source

Impact and Implications

The methodologies hold several significant impacts and implications for various machine-learning applications

1. Bridging the Gap Between Efficiency and Accuracy

Despite their superior accuracy, cross-encoders have often needed to be more suitable for large-scale applications due to their computational demands. Methods such as sparse-matrix factorization and the AXN adaptive retrieval algorithm address these limitations. Together, these techniques approximate cross-encoder performance with minimal accuracy loss while significantly enhancing scalability. As a result, systems such as search engines, recommendation platforms, and question-answering tools can now achieve high-quality retrieval without incurring prohibitive computational costs.

2. Improved Zero-Shot Retrieval Performance

The adaptive nature of the proposed AXN method enables it to improve retrieval recall, even when dealing with items unseen during training. This is particularly valuable in zero-shot retrieval scenarios, where models are tasked with generalizing to new domains or item sets. The ability to leverage existing DE models for initialization while avoiding the computational cost of full distillation-based training further enhances the applicability of these methods in practical settings.

3. Broad Applicability Across Tasks

The proposed methods are not limited to a specific task or domain. They can be applied to any application where k-NN search with CE models is beneficial, including information retrieval, question answering, entity linking, and recommendation systems. The generalizability of the techniques, combined with their efficiency advantages, positions them as valuable tools for a wide range of machine learning practitioners and researchers.

4. Scalable Deployment of Cross-Encoders

The framework unlocks cross-encoder scalability and enables their integration into real-world systems handling vast datasets. Techniques like offline indexing and iterative refinement allow these systems to manage millions or even billions of query-item pairs efficiently. This scalability is particularly transformative for industries such as e-commerce, where quick and accurate retrieval directly affects user satisfaction and revenue. With this approach, applications can deliver precise results even for expansive product catalogs.

5. Computational Efficiency for Large Datasets

Sparse-matrix factorization reduces computational overhead by strategically selecting query-item pairs for similarity score calculations. The system optimizes compact embeddings for reusability, ensuring that subsequent retrievals are highly efficient. This computational efficiency is invaluable for resource-constrained environments such as mobile devices or IoT systems. Applications like voice-activated search and personalized recommendations can now adopt advanced retrieval methods without sacrificing performance.

Conclusions and Future Directions

The proposed methodologies—sparse-matrix factorization, offline indexing, and the AXN adaptive k-NN search algorithm—redefine the scalability and efficiency of cross-encoder-based k-NN retrieval. The framework enables practical deployment in large-scale, real-world systems by addressing computational challenges while maintaining high precision. This innovation holds transformative potential for industries like e-commerce, healthcare, and information retrieval, offering highly relevant results on a massive scale.

Future Research Opportunities

Enhancing Multi-Modal Retrieval Capabilities: Future work can expand retrieval methods to support multi-modal data, such as text, images, and audio. To give you an idea, combining text and images could improve visual search in e-commerce while integrating audio and text might enable more effective voice-activated searches. These innovations could also support hybrid recommendation systems by using product descriptions, reviews, and images together. Developing cross-modal embeddings or unified models for these data types will be key to making these applications practical .
Integrating Graph-Based Indexing: Combining sparse-matrix factorization with graph-based indexing methods, known for their efficiency in large-scale searches, could improve retrieval scalability and performance.
Advancing Regularization Techniques: Developing more robust regularization methods could enhance the framework's ability to generalize in noisy or complex datasets, increasing its reliability across diverse environments.
Adapting to Dynamic Data: Exploring strategies to allow the framework to adjust as datasets evolve dynamically is crucial, especially for fast-changing platforms like social media or news aggregators.
Applying to Specialized Domains: The framework's capabilities can be tailored to fields like bioinformatics, legal research, and medical retrieval, where handling high-dimensional genomic or clinical data is critical.
Optimizing Sparse-Matrix Construction: Leveraging machine learning to identify high-impact query-item pairs during sparse-matrix construction could improve efficiency and accuracy.

Haziqa Sajid
Digital Storytelling for Data, AI, B2B & SaaS

Next: What is Voyager?

Content

Start Free, Scale Easily

Try the fully-managed vector database built for your GenAI applications.

Try Zilliz Cloud for Free