Decoding Softmax Activation Function
This article will discuss the Softmax Activation Function, its applications, challenges, and tips for better performance.
Read the entire series
- Introduction to Unstructured Data
- What is a Vector Database and How Does It Work?
- Understanding Vector Databases: Compare Vector Databases, Vector Search Libraries, and Vector Search Plugins
- Introduction to Milvus Vector Database
- Milvus Quickstart: Install Milvus Vector Database in 5 Minutes
- Introduction to Vector Similarity Search
- Everything You Need to Know about Vector Index Basics
- Scalar Quantization and Product Quantization
- Hierarchical Navigable Small Worlds (HNSW)
- Approximate Nearest Neighbors Oh Yeah (Annoy)
- Choosing the Right Vector Index for Your Project
- DiskANN and the Vamana Algorithm
- Safeguard Data Integrity: Backup and Recovery in Vector Databases
- Dense Vectors in AI: Maximizing Data Potential in Machine Learning
- Integrating Vector Databases with Cloud Computing: A Strategic Solution to Modern Data Challenges
- A Beginner's Guide to Implementing Vector Databases
- Maintaining Data Integrity in Vector Databases
- From Rows and Columns to Vectors: The Evolutionary Journey of Database Technologies
- Decoding Softmax Activation Function
- Harnessing Product Quantization for Memory Efficiency in Vector Databases
- How to Spot Search Performance Bottleneck in Vector Databases
- Ensuring High Availability of Vector Databases
- Mastering Locality Sensitive Hashing: A Comprehensive Tutorial and Use Cases
- Vector Library vs Vector Database: Which One is Right for You?
- Maximizing GPT 4.x's Potential Through Fine-Tuning Techniques
- Deploying Vector Databases in Multi-Cloud Environments
- An Introduction to Vector Embeddings: What They Are and How to Use Them
Decoding Softmax Activation Function
This article will discuss the Softmax Activation Function, its applications, challenges, and tips for better performance. We'll explore its mathematical foundations, compare it with other activation functions, and provide practical implementation examples.
Introduction to Activation Functions
Activation functions introduce non-linearity in a neural network (NN) to transform raw inputs into meaningful outputs. Without non-linearity, a neural network is a linear regression model, simply passing the result of one neuron to another. Activation functions allow neural networks to learn complex patterns by deciding which neurons are crucial for decision-making and activating them to pass to the next layer.
What is Softmax Activation Function?
The Softmax function, also known as the normalized exponential function, is a popular activation function primarily used for multi-class classification. While other activation functions, like the Sigmoid activation function mentioned earlier, are limited to binary classification use cases, the softmax function works on multiple classes of labels.
The Softmax function takes an input vector of raw outputs from a neural network and scales them into an array of probabilities. In the probability array, each probability represents the likelihood of the presence of each class label, and the array sums up to one. The class with the highest probability is chosen as the final prediction by the neural network.
The formula of the Softmax Activation function is:
f(xi) = e^xi / Σj e^xj
Where:
x = Vector of raw outputs from the previous layer of a neural network
i = Probability of class i
e = 2.718
Scaling logits into probabilities adding their values up to one enhances the interpretability of a model’s predictions. These probabilities can be interpreted as confidence scores, enforcing a decision where a model picks the class with the highest probability.
Mathematical Intuition
To understand why the Softmax function works, let's break it down:
Exponentiation: By applying e^x to each input, we ensure all values are positive. This step also amplifies differences between inputs.
Normalization: Dividing by the sum of all exponentiated values ensures the output sums to 1, creating a valid probability distribution.
Relative scale: The exponential nature of the function preserves the relative scale of the inputs while mapping them to probabilities.
Visualizing the Softmax Equation
Keeping the mathematical formula in view, the Softmax function transforms logits into probabilities in the following steps:
Calculate the exponent of each entry in the raw vector, which denotes the output layer vector of final layer of a neural network. After exponentiation, higher scores become more prominent, while lower scores are further minimized, indicating which scores to activate.
Step 1 Calculate exponents
Step One: Divide the exponent of probability distribution of each entry by the sum of exponents of all entries. This normalizes probabilities sum of the exponentiated values into probabilities.
Step Two: Divide each exponent by sum of exponents
Step 2 Divide each exponent by sum of exponents
- The values after the normalization represent the output probabilities for each class. These are arranged into a vector, representing the final Softmax output.
Step Three Arrange probabilities in vector
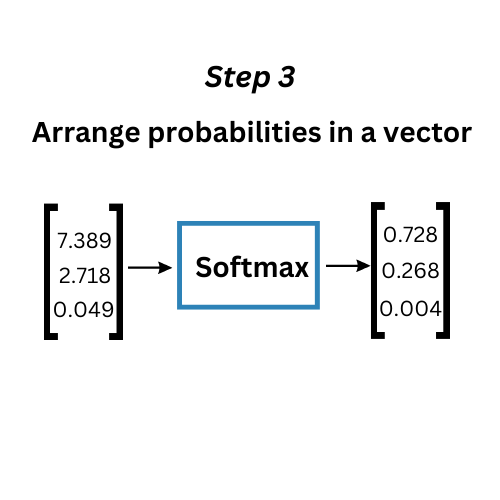Step 3 Arrange probabilities in vector
Implementing the Softmax Function in Python
Implementing the Softmax function in Python is straightforward. Let's have a look at how we can do it in TensorFlow and PyTorch, respectively:
- Softmax Function in TensorFlow
In TensorFlow, implementing the Softmax Activation Function is as simple as defining the output layer with Softmax function:
from tensorflow.keras import layers
# Define the output layer with softmax activation
output_layer = layers.Dense(num_classes, activation="softmax")(hidden_layer_output)
# Compile the model
model.compile(loss="categorical_crossentropy", optimizer="adam", metrics=["accuracy"])
The above snippet defines the following:
num_classes: The number of categories in your dataset.
hidden_layer_output: The output of the previous layer (the final hidden layer in most cases).
activation=”softmax”: Specifies the model to use Softmax as an activation function.
Alternatively, nn.softmax function in TensorFlow allows more direct control:
import tensorflow as tf
# Apply softmax to the logits
predictions = tf.nn.softmax(logits, axis=-1)
Where:
logits: Output of the final hidden layer.
axis=-1: Specifies applying Softmax function in the last dimension.
- Softmax Activation Function in PyTorch
Similar to TensorFlow, PyTorch offers a Softmax function for a simple implementation:
import torch
# Apply softmax to the logits
predictions = torch.nn.functional.softmax(logits, dim=1)
Where:
logits: Output of the final hidden layer.
axis=1: Specifies applying Softmax in the last dimension.
A dedicated Softmax layer can also be created in PyTorch using nn.Softmax function:
import torch.nn as nn
# Create a softmax layer
softmax_layer = nn.Softmax(dim=1)
# Pass the output through the layer
predictions = softmax_layer(logits)
Where:
- dim=1: Specifies applying Softmax along dimension 1.
Applications of Softmax Activation Function in Artificial Intelligence (AI)
Softmax activation function solves real-world multi-class machine learning problems. Some of them include:
- Image Classification
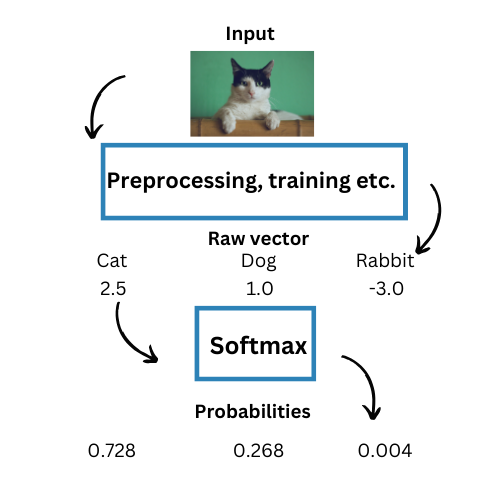
Neural networks excel at image classification, analyzing and categorizing an input image into predefined classes. The softmax function plays a vital role in this process, assigning a probability to each class based on its learning. The class with the highest probability is picked as the model’s final output.
For example, consider a Convolutional Neural Network (CNN) that uses the Softmax function in its final layer. The task is to classify images into “Cat”, “Dog”, and “Rabbit”. Suppose the probabilities assigned to each vector components each class are [0.728, 0.268, 0.004]. In this case, the softmax output vector with highest probability is assigned to “Cat”; hence, it will be the final output.
- Sentiment Analysis
Twitter sentiment analysis is a well-known application of the Softmax function. Furthermore, AI headline analyzers have emerged recently to identify whether a headline is positive, negative, or neutral. Softmax activation function makes this possible under the hood.
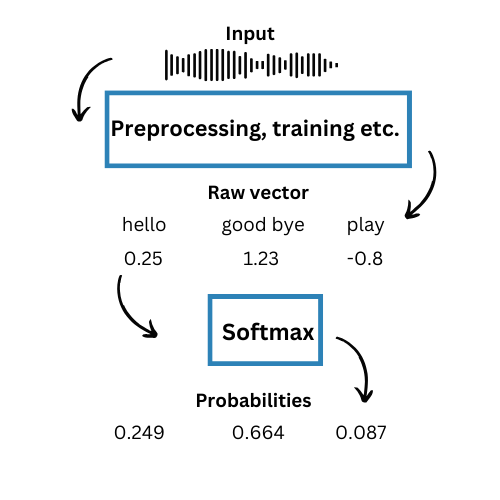
- Speech Recognition
AI chatbots must accurately identify users’ words from input array of predefined alternatives and formulate their responses accordingly. So, the model analyzes the input audio and generates a score for maximum value for each possible word. The Softmax function can compute values and then assigns probabilities to each alternative. For example:
Challenges and Best Practices of Softmax
Considering the challenges of an activation function beforehand ensures accurate and efficient classification. Taking preventive measures will improve model accuracy. While Softmax function is robust for multi-class and classification tasks, it has its limitations. However, we can mitigate these limitations by following best practices and ensuring efficient performance.
- Imbalanced Dataset
Datasets, where one class outnumbers others, mislead Softmax activation. This results in the majority class receiving a higher probability, even if the contrary is the case.
Best Practices: Removing some records from the majority class or duplicating some records from oversampling the minority class results in balanced datasets. Cost functions that heavily penalize misclassifications can prompt)) the model to learn minority classes and achieve accurate probabilities.
- Numerical Instability
When logits are large, their exponentials may result avoid overflow, in extremely large numbers. Contrarily, when logits are extremely small, their exponentials can become close to zero. These could lead to overflow errors and inaccurate output values and probability distributions, along with other numerical stability and instability.
Best Practices: Normalizing data to the largest value on a consistent scale prevents numerical instability. The Log-Softmax function can also be used to mitigate the challenges of overflow errors. It works by computing the logarithm of the two Softmax values and output, converting them into smaller numbers.
Relationship with Cross-Entropy Loss
Softmax is often used in conjunction with cross-entropy loss for training multi-class classification models. The cross-entropy loss function is particularly well-suited for use with Softmax because:
It measures the dissimilarity between the predicted probability distribution and the true distribution.
It provides a smooth, convex optimization landscape when used with Softmax.
The formula for cross-entropy loss with Softmax is:
L = -Σ_i y_i * log(softmax(x_i))
Where y_i is the true label (usually one-hot encoded) and softmax(x_i) is the predicted probability for class i.
Conclusion
The Softmax activation function is widely used due to its simplicity and interpretability. It guides accurate decision-making by assigning softmax values or probabilities to each class in a dataset, making the highest probability class suitable as an output.
Understanding how the softmax function works is crucial in AI and classification tasks. It transforms raw neural outputs into normalized probabilities that sum to one, enabling reliable decision-making in various applications. While best practices exist to combat the challenges of any tool, a trade-off always exists. Understanding its functionality and best practices allows for making appropriate trade-offs and leveraging it to its highest potential.
Use Softmax function in real-world projects and experiment with its applications for a deeper understanding.
Other Resources: A list of Neural Network Activation functions
To better understand Softmax, let's compare it with other common activation functions:
Binary Step Function
A binary step function is an activation function used in neural networks that determines whether a neuron should be activated based on a threshold value. When the input to the function exceeds the threshold, the neuron is activated and outputs a value of 1; otherwise, it is deactivated, outputting a value of 0. This function effectively decides whether the neuron's output values should be passed on to the next layer in the network.
Linear
An activation function (sometimes referred to as a "no activation" function) that returns real value of its input multiplied by a specified value.
RelU
The ReLU (Rectified Linear Unit) function is an activation function commonly used in neural networks. It outputs the input directly if it's positive, and outputs zero if the input is negative. Although it behaves like a linear function for positive inputs, ReLU is non-linear because it introduces a zero output for negative values.
One key feature of ReLU is that it allows for efficient backpropagation due to its simple derivative, which is either 1 or 0, depending on the input. This makes ReLU computationally efficient and helps in training deep networks.
Importantly, ReLU doesn't activate all neurons simultaneously—only those with a positive output from the linear transformation are activated. Neurons with a negative input are deactivated, effectively outputting zero and not passing any signal forward.
Tanh
An activation function that returns the hyperbolic tangent of its input vector. This function should not be used in hidden layers as they increase the model's susceptibility to training issues, such as vanishing gradients.
Formula: tanh(x) = (e^x - e^(-x)) / (e^x + e^(-x))
Use case: Hidden layers, but less common than ReLU
Limitation: Can suffer from vanishing gradients
Sigmoid (Logistic)
An activation function that returns the sigmoid function of its input. This sigmoid function should not be used in hidden layers as they increase the model's susceptibility to training issues, such as vanishing gradients.
Formula: σ(x) = 1 / (1 + e^(-x))
Use case: Binary classification
Limitation: Output range [0,1] for a single class
ELU
The Exponential Linear Unit (ELU) is an activation function used in neural networks that is a variant of the ReLU function. Unlike ReLU, which outputs zero for negative inputs, ELU modifies the slope of the negative part of the function using an exponential curve. Specifically, for negative input values, ELU outputs a smooth, curved value rather than a flat zero, which helps to reduce the "dead neuron" problem seen with ReLU.
In contrast to Leaky ReLU and Parametric ReLU, which introduce a small, constant slope (a straight line) for negative inputs, multiple outputs, ELU applies a logarithmic curve for negative values. This curve allows ELU to push the mean of activations closer to zero, which can help speed up machine learning, and make the model more robust to changes in input.
References:
Pearce, Brintrup, and Zhu. "Understanding Softmax Confidence and Uncertainty" arXiv 2021
Bridle. "Training Stochastic Model Recognition Algorithms as Networks can Lead to Maximum Mutual Information Estimation of Parameters" Neurips 1989
Haziqa SajidDigital Storytelling for Data, AI, B2B & SaaS
- Introduction to Activation Functions
- What is Softmax Activation Function?
- Visualizing the Softmax Equation
- Implementing the Softmax Function in Python
- Applications of Softmax Activation Function in Artificial Intelligence (AI)
- Challenges and Best Practices of Softmax
- Relationship with Cross-Entropy Loss
- Conclusion
- Other Resources: A list of Neural Network Activation functions
- **References:**
Content
Start Free, Scale Easily
Try the fully-managed vector database built for your GenAI applications.
Try Zilliz Cloud for Free