What is Backpropagation?
What is Backpropagation?
Backpropagation in Neural Networks
If you've walked around San Francisco lately, you will notice that there are a lot of autonomous vehicles from Waymo and Zoox not only driving the streets but picking up and dropping off passengers all day and night. These vehicles politely observe traffic rules, avoid any mishaps with other cars, and manage to navigate the crowds of people during busy times of the day. For people not used to this sight, it is amazing to see these armies of vehicles doing their job!
 Autonomous Car in San Francisco
Autonomous Car in San Francisco
A process in machine learning called backpropagation allows these vehicles to navigate these complex situations. But what exactly is backpropagation, and how does it enable such sophisticated behavior?
At its core, backpropagation is a highly efficient learning mechanism for artificial neural networks, heavily relying on the activation function to determine the output of neurons. Imagine a novice driver learning to navigate city streets. They might start off making mistakes—braking too hard, turning too sharply, or misjudging distances. With each error, they adjust their actions, gradually improving their skills. Backpropagation works in a similar way, but at lightning speed and with mathematical precision.
In machine learning, backpropagation is the behind-the-scenes teacher, constantly fine-tuning the decision-making process of AI systems. The input data flows through the layers of the neural network model during the training process, impacting the performance and efficiency of the neural network's training and error adjustment processes. It's not just limited to self-driving cars; this technique is the secret sauce behind many AI applications we encounter daily - from voice assistants that understand our accents to recommendation systems that seem to know our preferences better than we do, all thanks to the output layer generating the model's predictions.
In this post, we'll peel back the hidden layers of backpropagation, exploring how it transforms raw data into intelligent decisions. We'll break down the math without getting lost in equations, walk through a practical example you can relate to, and even show you how to implement this powerful technique using Python.
Whether you're a budding data scientist, a curious tech enthusiast, or simply someone fascinated by the AI revolution around us, understanding backpropagation will give you valuable insights into the machinery of modern AI. So, let's get into the heart of machine learning, where numbers dance with neurons to create the intelligent systems shaping our world.
What is the backpropagation algorithm?
Backpropagation is a backpropagation algorithm crucial in training feedforward neural networks, the workhorses of many AI applications.
Think of backpropagation as a relentless coach with a knack for data-driven improvement: A feedforward neural network utilizes recurrent backpropagation to adjust its weights and biases during training, ensuring optimal performance.
It's not a one-and-done process but a persistent cycle of refinement. With each training round (called an epoch), backpropagation analyzes the network's performance and makes precise adjustments. It's like a coach reviewing game footage after each play, tweaking strategies in real time.
The algorithm's goal? To minimize the 'cost function', reduce the gap between the AI's predictions and reality. It does this by fine-tuning the network's internal parameters (weights and biases), much like a mechanic adjusting the various components of an engine for optimal performance.
Backpropagation employs sophisticated optimization techniques, typically gradient descent or its close cousin, stochastic gradient descent. These methods help the network navigate the complex landscape of possible solutions, always moving towards better performance.
At its core, backpropagation leverages a fundamental principle of calculus: the chain rule. This mathematical tool allows the algorithm to traverse the neural network's intricate layers, determining how each component contributes to the overall error. It's akin to tracing a river back to its source, understanding how each tributary affects the main flow.
By combining iterative learning, smart optimization, and mathematical precision, backpropagation transforms neural networks from static structures into dynamic, self-improving systems. It's not just about making predictions; it's about constantly evolving to make better predictions, pushing the boundaries of what artificial intelligence can achieve.
 Backpropagation of neural networks
Backpropagation of neural networks
Backpropagation algorithms
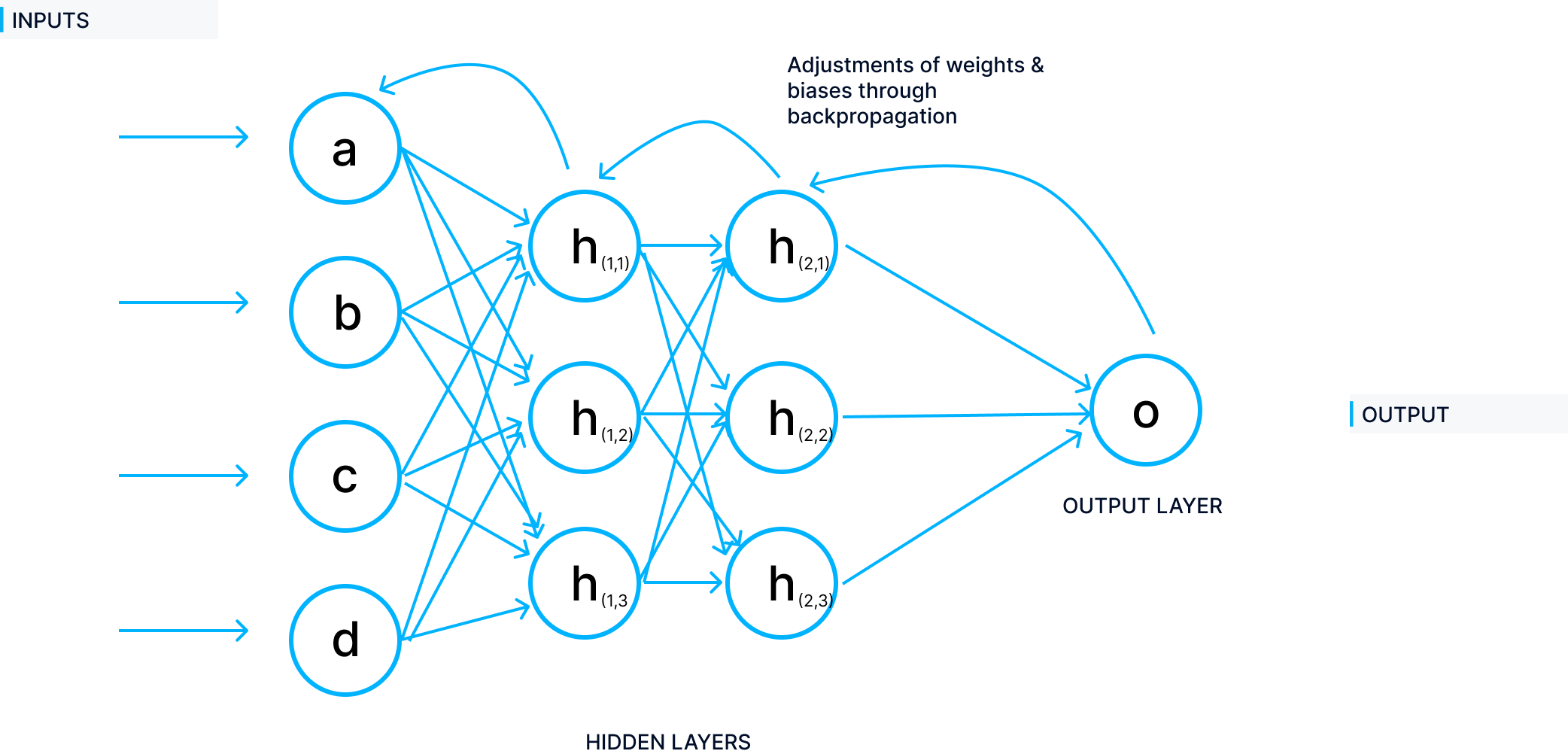
Mathematically, backpropagation is a sophisticated dance of calculus and optimization. At its core, it's about understanding how changes in a neural network's parameters affect its overall performance. The process begins with a loss function, quantifying the difference between the network's predictions and actual outcomes. This function acts as a compass, guiding the network towards better performance. The feedforward process pushes data through the network, with each neuron applying weights and biases before passing the result through an activation function.
Here's where calculus takes center stage: backpropagation calculates partial derivatives to determine how each weight and bias contributes to the overall error. The chain rule, a fundamental principle of calculus, allows these derivatives to be efficiently computed across multiple layers computing the gradient. The learning rate, a crucial hyperparameter, controls how quickly the network adjusts its parameters in response to these calculations. Too high, and the network might overshoot its optimal configuration; too low, and learning becomes painfully slow. This entire process is iterative, with each epoch (a full pass through the training data) refining the network's parameters. Over time, this mathematical machinery drives the network towards a configuration that minimizes the loss function, effectively teaching the AI to make increasingly accurate predictions.
Understanding the Backpropagation Algorithm
Backpropagation operates in two main phases:
1. Forward Pass:
Input data enters the network through the input layer.
Each neuron in subsequent layers calculates a weighted sum of its inputs, adds a bias, and applies an activation function.
Information flows through the network, with each layer's output becoming the next layer's input.
The final layer produces the network's prediction.
2. Backward Pass:
The network calculates the error between its prediction and the actual target.
This error signal propagates backwards through the network.
For each neuron, the algorithm computes how the error would change with small adjustments to weights and biases.
These calculations use the chain rule to determine the gradient of the error with respect to each parameter.
Weights and biases are adjusted to reduce the error.
Key Components:
- Activation Functions: Introduce non-linearity, enabling the network to learn complex patterns. Common choices include ReLU for hidden layers and softmax for classification outputs.
- Loss Function: Measures the difference between predictions and actual values. Mean squared error is often used for regression, while cross-entropy is common for classification.
- Learning Rate: Determines the size of weight updates. It requires careful tuning to balance learning speed and stability.
- Chain Rule: Allows efficient gradient calculation across multiple layers, helping the network attribute the final error to each of its parameters.
Backpropagation's effectiveness comes from its ability to adjust numerous parameters simultaneously, gradually improving the network's predictions over multiple iterations.
 Backpropagation
Backpropagation
An example of backpropagation in practice
Let's bring backpropagation to life with a practical example. Imagine we're all training neural networks with a simple AI to predict house prices in a bustling city neighborhood. Our neural network is like a rookie real estate agent learning the ropes of property valuation.
We start with a basic network architecture:
An input layer (think of it as the agent's eyes and ears).
A hidden layer (the agent's brain).
An output layer (the final price estimate).
Our dataset is a collection of recent home sales with features like square footage, number of bedrooms, and location.
In the forward and backward pass through, our AI agent looks at a house (inputs the features). It makes initial guesses about how important each feature is (applies weights) and adds some personal hunches (biases). After some internal calculations (activation functions), a price prediction is produced.
Now comes the reality check. Using a loss function, we compare squared error of the AI's prediction with the actual sale price. Let's say our agent overestimated by $50,000 - that's a big miss!
This is where backpropagation kicks in. It's like the agent's mentor, helping determine why the prediction was off. Working backward, it calculates how much each part of the decision-making process contributed to the error.
Based on this analysis, we update the weights and biases. Maybe our agent was putting too much emphasis on the number of bedrooms and not enough on the location. We make small adjustments to correct this.
This process repeats for many houses (iterations). Our AI agent gets a little smarter with each prediction and correction. Over time, its predictions start getting closer to the actual sale prices.
By the end of training, our AI has transformed from a rookie into a savvy property valuator, able to make accurate price predictions based on a home's features. That's backpropagation in action - turning raw data into valuable insights through continuous learning and refinement.

Cross-entropy loss* is used for training classification models. It’s an easy-to-implement loss function requiring labels encoded in numeric values for accurate loss calculation.*
Advantages of Backpropagation in Neural Networks
Backpropagation has become a fundamental algorithm in training neural networks due to several key advantages:
Accessibility: The algorithm doesn't require extensive mathematical background, making it approachable for newcomers to machine learning. Its straightforward implementation allows for easier debugging and modification.
Versatility: Backpropagation adapts well to various network architectures and problem domains. It can be applied effectively in feedforward networks, convolutional neural networks, and recurrent neural networks.
Efficient Learning: By directly calculating error gradients, backpropagation enables rapid weight adjustments. This efficiency is particularly valuable in deep networks where learning complex features can be time-consuming.
Generalization Capability: Through iterative weight updates, backpropagation helps networks identify underlying patterns in data. This leads to models that can make accurate predictions on new, unseen examples.
Scalability: The algorithm performs well across different dataset sizes and network complexities. This scalability makes it suitable for both small experiments and large-scale industrial applications.
These advantages have contributed to backpropagation's widespread adoption in neural network training. Its balance of simplicity and effectiveness makes it a valuable tool for developing machine learning models across various applications.
Backpropagation Implementation in Python
There are a number of cool python projects to help you to try backpropagation yourself.
Implementing Backpropagation in Python: Building a Neural Network from Scratch — Andres Berejnoi
How to Code a Neural Network with Backpropagation In Python (from scratch)
Backpropagation Applications
Backpropagation's influence extends far beyond theoretical machine learning, powering a multitude of AI applications that have become integral to our daily lives. Some of these applications include:
Autonomous Vehicles: As mentioned earlier with Waymo and Zoox, self-driving cars rely heavily on neural networks to interpret sensor data, predict traffic patterns, and make split-second decisions. Backpropagation enables these vehicles to learn from each journey, continuously improving their navigation and safety protocols.
Medical Diagnosis: AI systems are increasingly assisting healthcare professionals in interpreting medical images like X-rays, MRIs, and CT scans. Backpropagation allows these systems to learn from vast databases of medical images, often spotting subtle abnormalities that might escape the human eye.
Natural Language Processing: Beyond voice assistants, backpropagation powers machine translation services, sentiment analysis tools, and chatbots. These applications can understand context, nuance, and even sarcasm in written text, bridging language barriers and enhancing communication.
Recommendation Systems: Streaming services like Netflix and Spotify use neural networks to analyze your viewing or listening habits and suggest content you might enjoy. Backpropagation helps these systems learn from user interactions, continuously refining their recommendations.
Robotics: In manufacturing and research settings, robots use neural networks to learn complex tasks, from precise assembly operations to navigating unpredictable environments. Backpropagation allows these robots to refine their movements and decision-making processes over time.
These applications represent just a fraction of backpropagation's impact. As AI continues to evolve, this algorithm remains at the heart of innovations that are reshaping industries, advancing scientific research, and transforming our interaction with technology.

This post covers Natural Language Processing fundamentals that are essential to understanding all of today’s language models.
Challenges and Considerations:
While backpropagation has revolutionized machine learning, it's not without its challenges and considerations. Let's explore some of the key issues that researchers and practitioners grapple with:
Vanishing Gradient Problem: In deep neural networks, gradients can become extremely small as they're propagated back through the layers. This can lead to painfully slow learning or even a complete halt in training for the earlier layers. It's like trying to whisper a message through a long chain of people - by the time it reaches the end, the message might be lost.
Exploding Gradient Problem: The flip side of vanishing gradients, this occurs when gradients become extremely large, causing unstable updates to the network weights. It's akin to a small change in input causing a disproportionately large change in output, making the network unreliable.
Local Minima Traps: Backpropagation aims to find the global minimum of the loss function, but it can get stuck in local minima, leading to suboptimal solutions. Imagine trying to find the lowest point in a hilly landscape while blindfolded - you might think you've reached the bottom when you're actually just in a small dip.
Computational Intensity: Training large neural networks with backpropagation can be extremely computationally expensive, requiring significant time and resources. This can limit the accessibility of deep learning to those with access to powerful hardware.
Overfitting: With its ability to learn complex patterns, a network using backpropagation can sometimes learn the noise in the training data too well, leading to poor generalization on new data. It's like memorizing the answers to a test instead of understanding the underlying principles.
Hyperparameter Tuning: Choosing the right learning rate, batch size, and network architecture can be more art than science, often requiring extensive experimentation. It's a delicate balance - too aggressive, and the model might never converge; too conservative, and training might take an impractically long time.
Non-Differentiable Activation Functions: Backpropagation relies on calculating gradients, which becomes problematic with non-differentiable activation functions like the step function. This limits the types of neural architectures that can be easily trained.
Catastrophic Forgetting: When training on new data, neural networks can rapidly forget previously learned information. This is particularly challenging in scenarios requiring continuous learning.
Interpretability Issues: The complex nature of deep neural networks makes it difficult to interpret why a network made a particular decision. This "black box" nature can be problematic in applications requiring transparency, like healthcare or finance.
Data Dependency: Backpropagation's effectiveness is heavily reliant on the quality and quantity of training data. In scenarios with limited or biased data, the algorithm may struggle to learn effectively or may perpetuate existing biases.
Addressing these challenges is an active area of research in the machine learning community. Techniques like batch normalization, residual connections, and adaptive learning rates have been developed to mitigate some of these issues. As the field progresses, new innovations continue to push the boundaries of what's possible with backpropagation and neural networks.
Future Implications:
As we peer into the future of AI, backpropagation stands at a fascinating crossroads. While it remains a cornerstone of deep learning, emerging trends suggest a landscape of both evolution and revolution. Here's a glimpse into what the future might hold:
Quantum Backpropagation: With the rise of quantum computing, researchers are exploring quantum versions of backpropagation. These could potentially solve optimization problems exponentially faster than classical methods, opening doors to training vastly more complex networks.
Neuromorphic Computing: As AI hardware evolves to more closely mimic biological brains, we might see new forms of backpropagation that are more energy-efficient and capable of real-time learning, similar to how our brains continuously adapt.
Federated Learning: Future backpropagation algorithms might enable better privacy-preserving AI, allowing models to learn from distributed datasets without centralizing sensitive information. This could revolutionize areas like healthcare AI, where data privacy is paramount.
Explainable AI: As the demand for AI transparency grows, we may see new backpropagation techniques that not only optimize performance but also provide clearer insights into the decision-making process of neural networks.
Meta-Learning: Future backpropagation might not just optimize model parameters, but also learn how to learn. This could lead to AI systems that adapt to new tasks with minimal training, similar to human intuition.
Continuous Learning Systems: Advancements in backpropagation could solve the challenge of catastrophic forgetting, leading to AI systems that learn continuously throughout their operational lifetime, constantly improving without losing previously acquired knowledge.
Hybrid Learning Approaches: We might see backpropagation combined with other learning paradigms, like reinforcement learning or evolutionary algorithms, creating more robust and versatile AI systems.
Emotional and Social Intelligence: Future backpropagation techniques could help AI systems better understand and respond to human emotions, potentially leading to more empathetic and socially intelligent AI assistants.
Environmental Adaptation: As AI systems are deployed in diverse and unpredictable environments, new forms of backpropagation might enable rapid adaptation to changing conditions, crucial for applications like disaster response robots or climate monitoring systems.
Ethical AI Training: Future backpropagation algorithms might incorporate ethical considerations directly into the learning process, helping to create AI systems that are not just intelligent, but also aligned with human values and societal norms.
These potential advancements suggest a future where backpropagation evolves beyond its current form, continuing to drive AI innovation in ways we're only beginning to imagine. As with all technological predictions, some of these may materialize while others give way to entirely unforeseen developments. What's certain is that the principles behind backpropagation will continue to shape the trajectory of AI for years to come.
Interdisciplinary Relevance with Vector Databases:
Backpropagation's influence extends across numerous disciplines, with vector databases playing a crucial supporting role:
Cognitive Neuroscience: Simulating neural processes to understand human cognition.
Computational Linguistics: Revolutionizing language processing and generation.
Computer Vision: Enhancing image interpretation for medical imaging and autonomous vehicles.
Bioinformatics: Predicting protein structures and gene functions.
Finance: Powering predictive models for market trends and risk assessment.
Robotics: Helping robots adapt to new environments.
Materials Science: Predicting material properties and designing new compounds.
Climate Science: Creating complex climate models and analyzing weather patterns.
Recommender Systems: Refining user preferences for personalized content delivery.
Cybersecurity: Detecting anomalies and potential threats in network traffic.
Vector databases enhance these applications by efficiently storing and retrieving high-dimensional data, crucial for neural networks trained via backpropagation. This synergy enables faster training, more efficient inference, and the ability to work with larger, more complex datasets.
As AI and machine learning continue to evolve, the interdisciplinary applications of backpropagation, supported by vector databases, promise to unlock new frontiers across an expanding range of fields, from quantum computing to creative AI systems.
- Backpropagation in Neural Networks
- What is the backpropagation algorithm?
- Backpropagation algorithms
- Understanding the Backpropagation Algorithm
- An example of backpropagation in practice
- Advantages of Backpropagation in Neural Networks
- Backpropagation Implementation in Python
- Backpropagation Applications
- Challenges and Considerations:
- Future Implications:
- Interdisciplinary Relevance with Vector Databases:
Content
Start Free, Scale Easily
Try the fully-managed vector database built for your GenAI applications.
Try Zilliz Cloud for Free