Activation Functions in Neural Networks
Activation Functions in Neural Networks
Activation Functions.png
Recent advancements in artificial intelligence (AI ) have been incredible, particularly in image recognition, natural language processing (NLP), and self-driving cars. A key factor contributing to these achievements is the ability of artificial neural networks to estimate complex, non-linear functions often present in real-world data. This capability is primarily attributed to activation functions, which introduce non-linearity into neural networks, allowing them to model complex relationships and patterns.
Let's understand activation functions in depth, their purpose, how they work, and why they are important for neural networks.
What are Activation Functions?
Activation functions are mathematical functions used in neural networks to determine the output of a neuron, introducing non-linearity into the model. They are applied to the inputs of nodes (neurons), the fundamental units of a neural network, to produce the node's output. A neural network computes the weighted sum of inputs, adds a bias, and then passes this sum through the activation function, which outputs a modified value. This value is passed to the next network layer or becomes the final output.
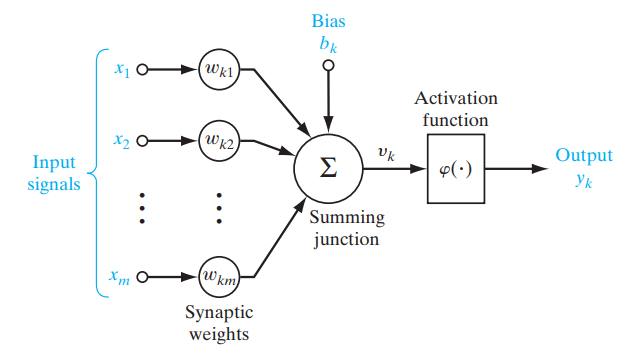Figure- Role of an activation function in a neural network. .png
Figure: Role of an activation function in a neural network. | Source
Why Non-Linearity Matters?
To understand why activation functions are essential, it’s important to know why linear models have limitations. A linear model represents a straight-line relationship between inputs and outputs. It works well in simple tasks but fails where data is more complex and has non-linear patterns.
Non-linearity allows neural networks to create decision boundaries that are not straight lines. Therefore, neural networks can understand non-linear patterns in data that cannot be represented by linear models.
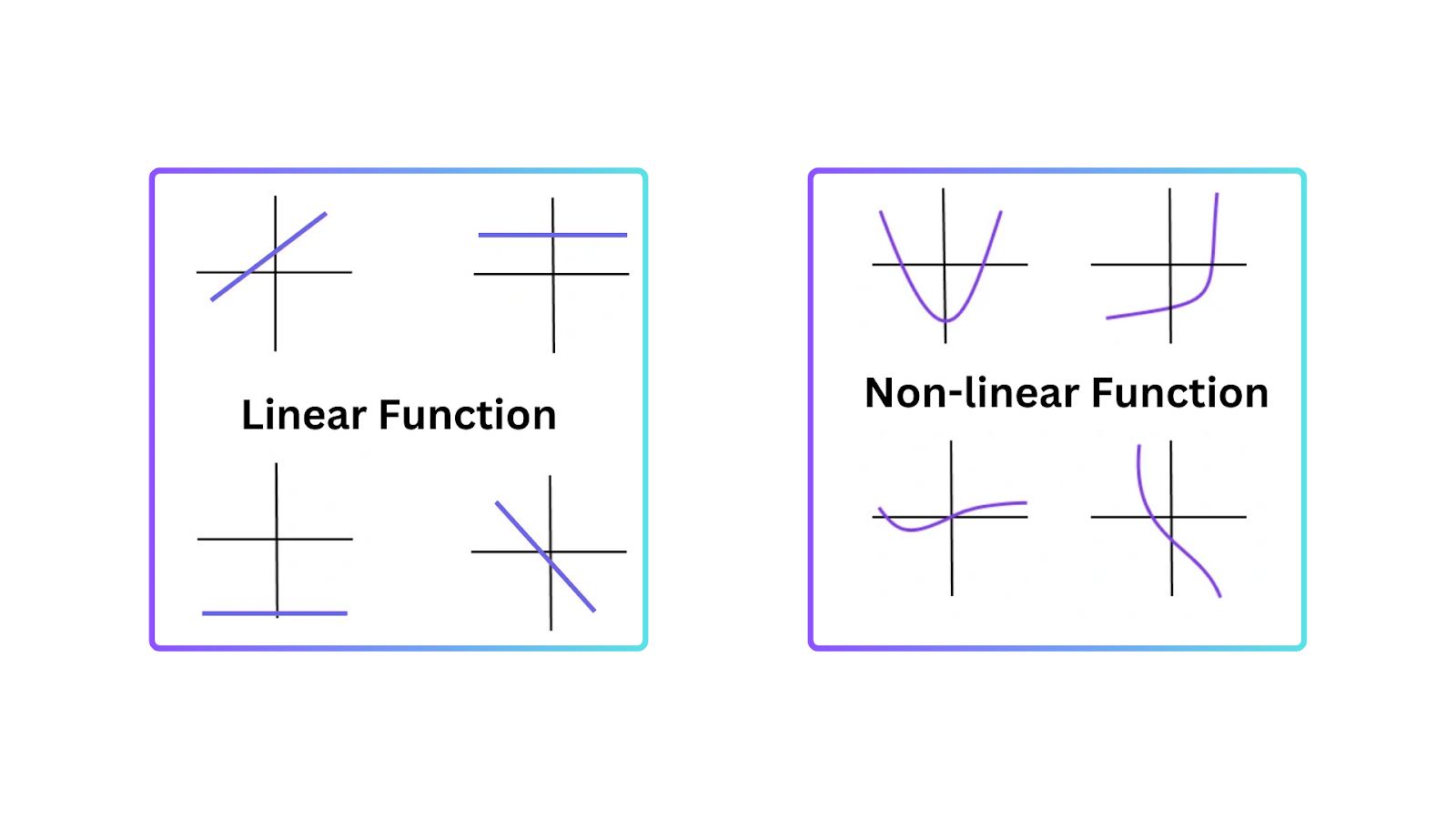Figure- Types of Functions.png
Figure: Types of Functions
How Activation Functions Work
Now that we’ve introduced activation functions let’s see how these functions work mathematically to convert the input signal into an output signal, a range often between 0 and 1 or -1 and 1. At each neuron in a neural network, data flows through in the following steps:
Input: Each neuron in a neural network receives one or more inputs. These inputs can come from the original data feeding into the network (in the case of the input layer) or from the outputs of neurons in the previous layer.
Weighted sum calculation: The inputs are multiplied by corresponding weights to determine their importance. Then, the weighted inputs are summed up, and a single value is returned, known as the weighted sum.
Activation function application: Once the weighted sum is calculated, it is passed through an activation function, and the result of the activation function becomes the neuron's output.
This process repeats in each neuron across network layers to change the data in more complex ways.
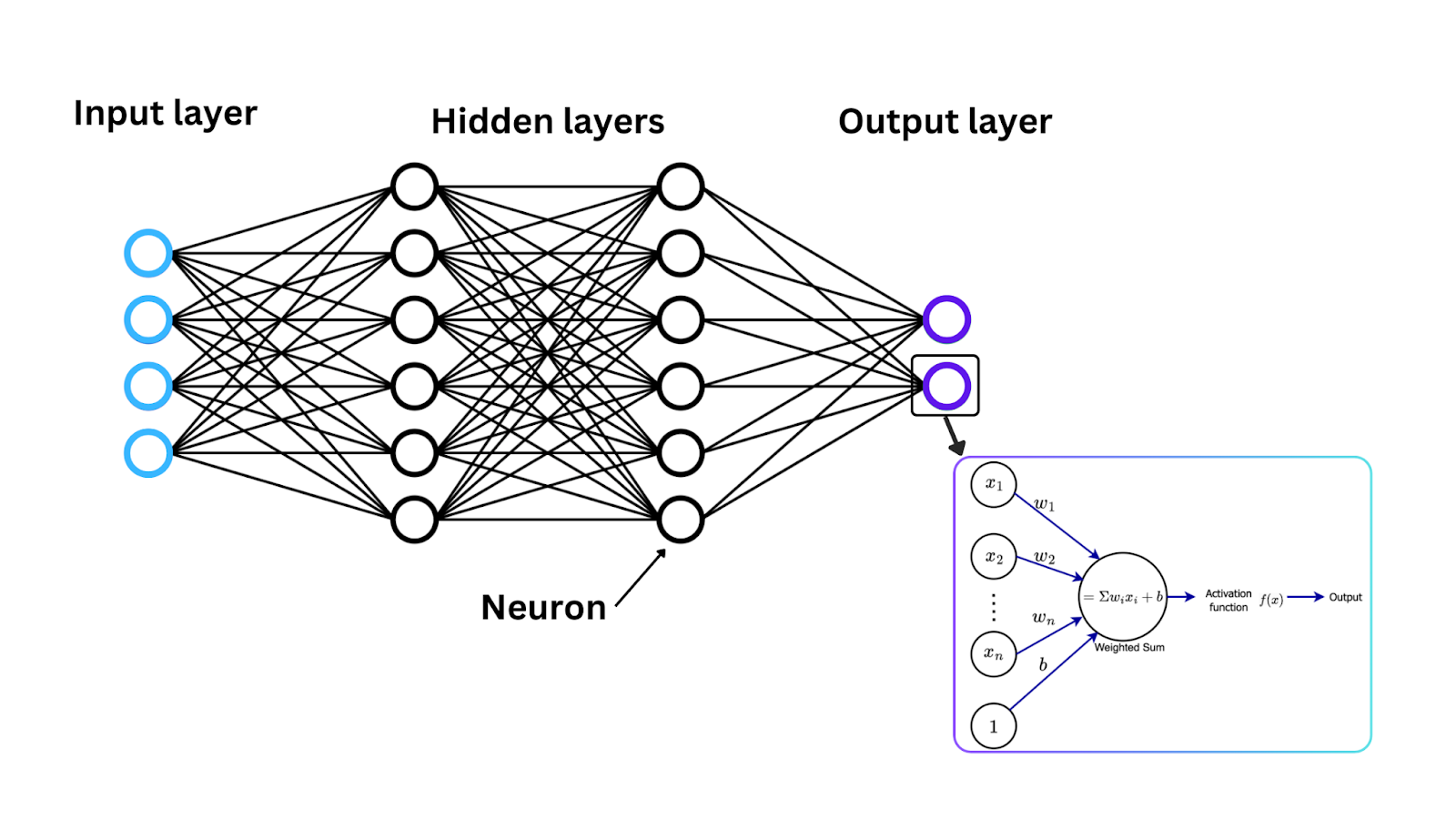Figure- Neural network architecture, activation function, and neuron weight updates. .png
Figure: Neural network architecture, activation function, and neuron weight updates.
Neural networks use different types of activation functions. Each function has its own strengths and is better suited for specific tasks. For instance, the sigmoid function is optimal for binary classification problems, softmax is useful for multi-class prediction, and ReLU helps overcome the vanishing gradient issue.
Choosing the right activation function speeds up training and improves performance. Now, Let’s look at some of the common activation functions:
Sigmoid Activation
ReLU (Rectified Linear Unit) Activation
Tanh (Hyperbolic Tangent) Activation
Leaky ReLU Activation
Sigmoid Activation
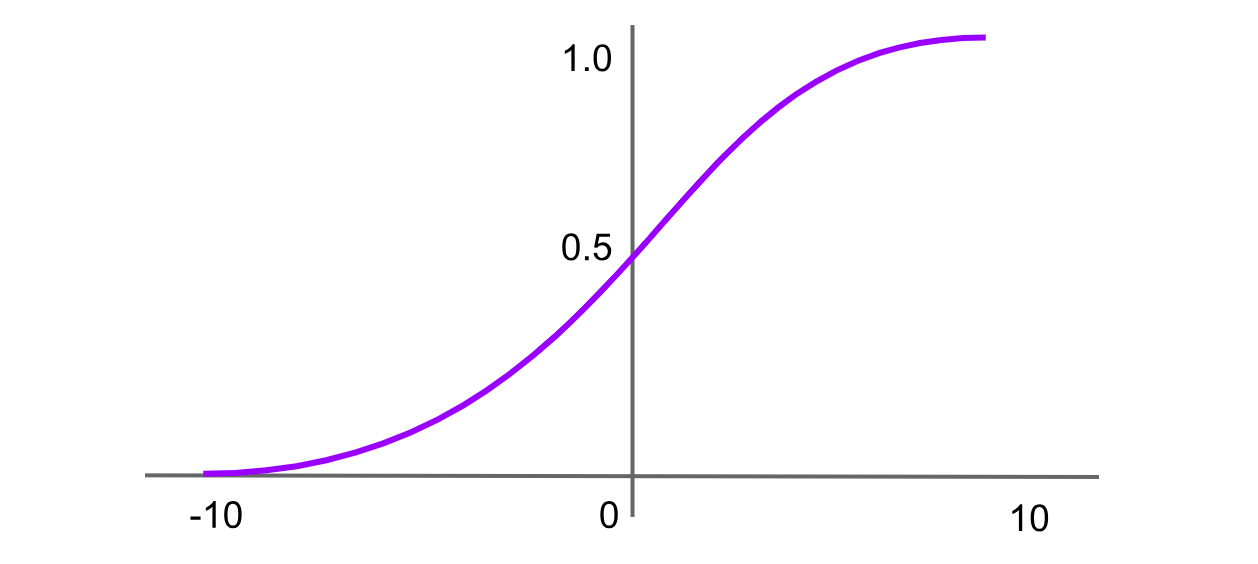Figure- Sigmoid activation function.png
Figure: Sigmoid activation function
The sigmoid function, also known as the logistic function, is one of the earliest and most widely known activation functions. It maps any input value to a range between 0 and 1, producing an "S"-shaped curve. The formula for the sigmoid function is:
Sigmoid = σ(x) = 1 / (1 + exp(-x))
Here is the code for defining the sigmoid function in Python.
import numpy as np
def sigmoid_function(x):
z = (1/(1 + np.exp(-x)))
return z
Sigmoid functions are useful for models where we need to predict the probability as an output. For example, in binary classification problems, we want the output to be interpreted as a probability between 0 and 1.
However, the Sigmoid has a vanishing gradient problem. During backpropagation (when the network learns by updating weights), sigmoid gradients become very small, which causes slow learning for deeper layers.
Softmax Activation
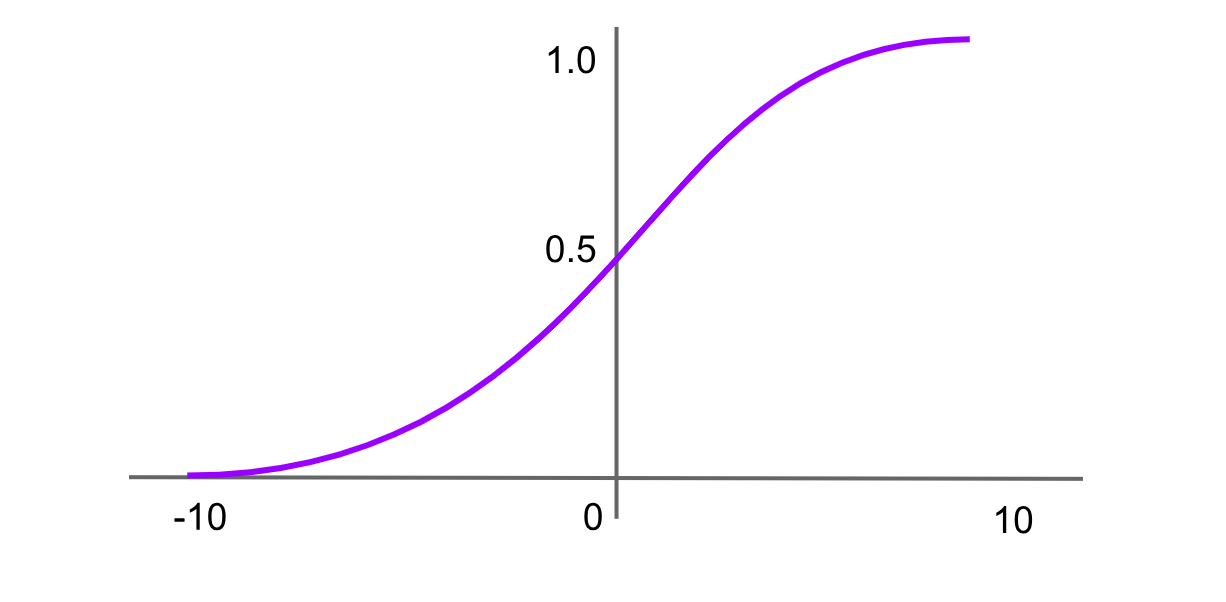Figure- Softmax activation function.png
Figure: Softmax activation function
The softmax function is commonly used in the output layer of neural networks for multi-class classification problems. It takes a vector of real numbers as input and normalizes it into a probability distribution over the classes. Each output is between 0 and 1, and all outputs sum to 1. The formula for the softmax function is:
Softmax(x)=f(xi)= exp(x) / sum(exp(x))
Let's code this in Python.
def softmax_function(x):
z = np.exp(x)
z_ = z/z.sum()
return z_
However, Softmax can be computationally expensive, especially in large networks, as it requires computing exponentials and normalizing them through all outputs.
ReLU (Rectified Linear Unit) Activation
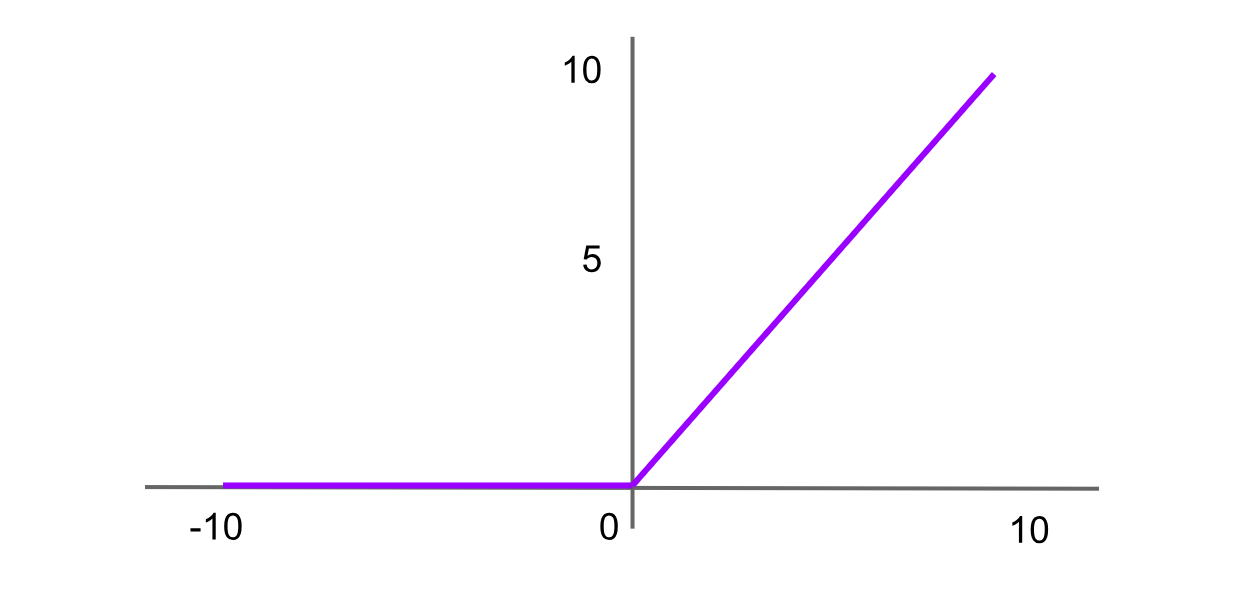Figure- ReLU activation function.png
Figure: ReLU activation function
ReLU is one of the most widely used activation functions in advanced neural networks. It returns 0 for any negative input, and for positive values, it returns the value itself. The formula for the ReLU function is:
ReLU = f(x) = max(0,x)
Here is the Python function for ReLU:
def relu_function(x):
if x<0:
return 0
else:
return x
ReLU is used in hidden layers of neural networks, particularly in computer vision tasks. It is computationally efficient because it does not have exponential or division operations. Compared to sigmoid, it's also less affected by the vanishing gradient problem. However, there is one downside of ReLU, which is the “dying ReLU” problem. If a neuron consistently outputs zero for all inputs, it becomes inactive and can no longer contribute to learning.
Tanh (Hyperbolic Tangent) Activation
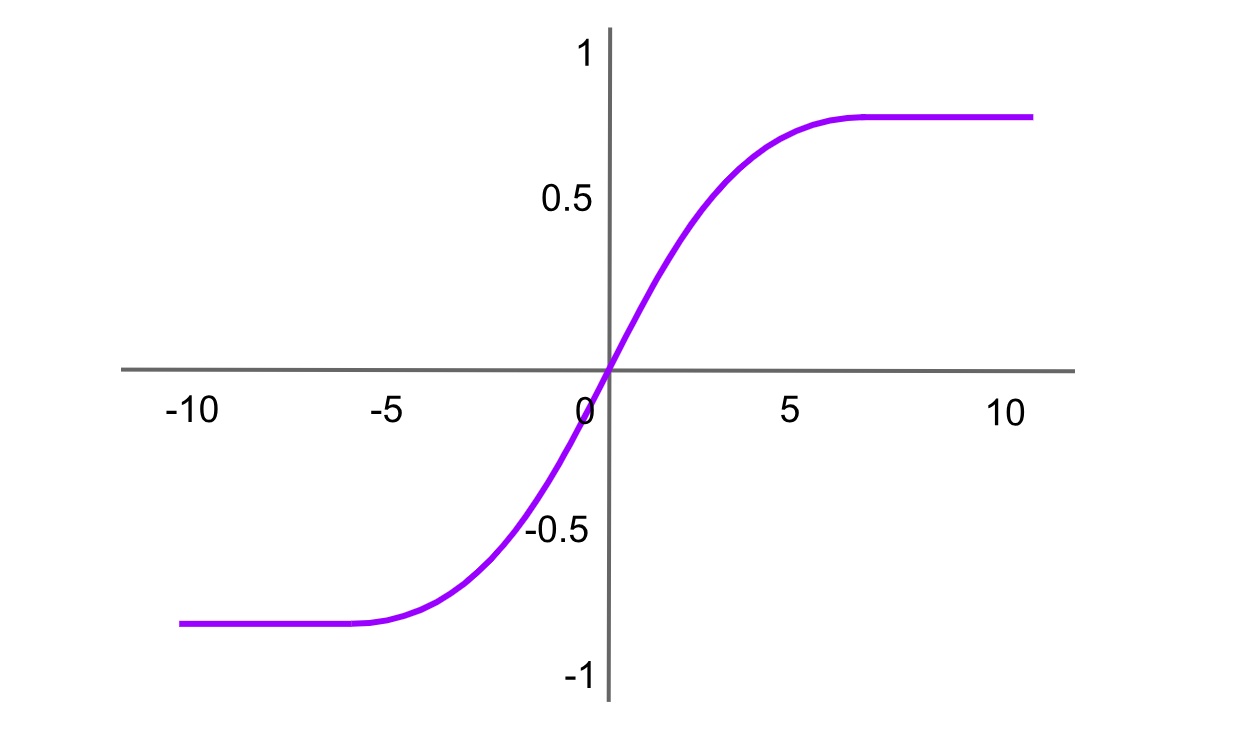Figure- Tanh activation function .png
Figure: Tanh activation function
The hyperbolic tangent function is similar to the sigmoid function but outputs values between -1 and 1. The formula for the Tanh function is:
tanh(x)= f(x)= 2 / (1+exp (−2x ))−1
Or
tanh(x)= f(x)=2sigmoid(2x)-1
Here is the Python code for the same:
def tanh_function(x):
z = (2/(1 + np.exp(-2*x))) -1
return z
Hyperbolic tangent is used in hidden layers of neural networks, particularly in natural language processing (NLP) tasks. It shares some similarities with the sigmoid function but has the advantage of being zero-centered, which can speed up learning in certain networks. However, like the sigmoid function, tanh is also affected by the vanishing gradient problem.
Leaky ReLU Activation
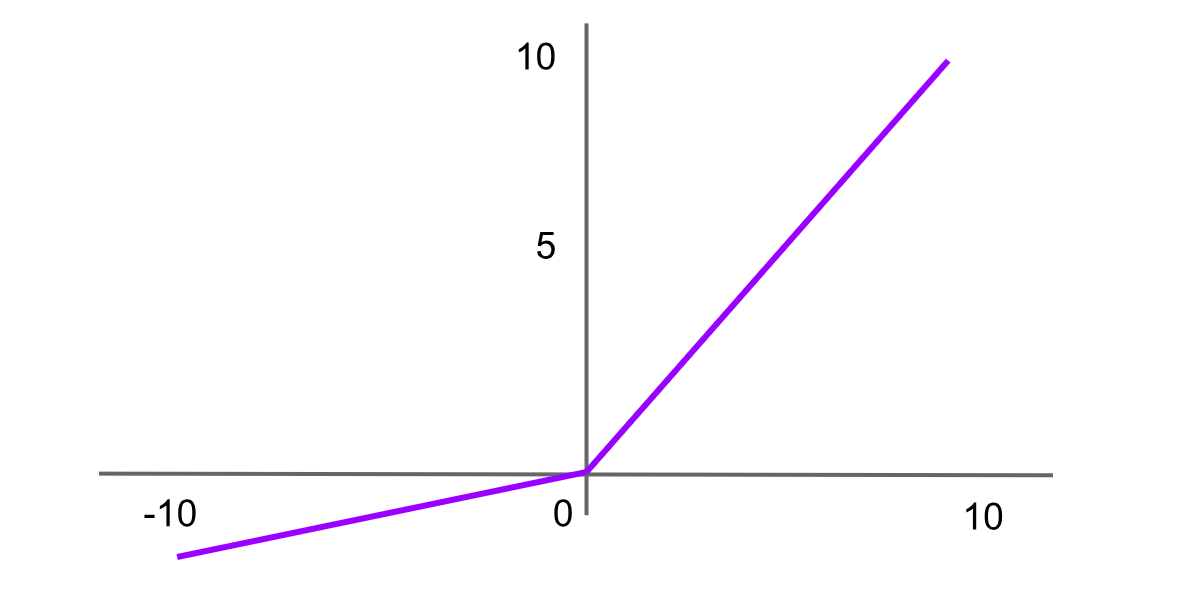Figure- Leaky ReLU activation function .png
Figure: Leaky ReLU activation function
Leaky Rectified Linear Unit, or Leaky ReLU, is a variant of ReLU designed to solve the “dying ReLU” problem by introducing a small slope for negative values instead of a flat slope. This helps neurons to continue learning instead of being permanently inactive. The formula for the Leaky ReLU function is:
Leaky ReLU = f(x)=max(αx,x)
Here, 𝛼 α is a small positive constant (e.g., 0.01) to ensure the neuron outputs a small negative value instead of zero for negative inputs. Since Leaky ReLU is a variant of ReLU, the Python code can be implemented with a minor modification.
def leaky_relu_function(x):
if x<0:
return 0.01*x
else:
return x
Comparison
To get a more better understanding of the activation functions, it's helpful to compare them with other key components of neural networks:
Activation Functions vs. Loss Functions
Activation functions define how the neurons in a network respond to incoming signals. They are applied to the outputs of neurons (or layers) to introduce non-linearity, which helps the network understand patterns and relationships in the data.
On the other hand, Loss functions are used to determine how well the neural network's predictions match the actual target values (the ground truth). They calculate the error between the predicted output and actual outcomes. Additionally, Optimization algorithms adjust the network's weights during training to minimize this error. Loss function includes:
Mean Squared Error (MSE) is commonly used for regression tasks.
Cross-entropy loss is used for classification tasks.
Activation Functions vs. Normalization
Activation functions control how the data moves from one layer to another and how neurons "fire" based on inputs.
However, Normalization, such as Batch normalization, helps to make training more effective. They work by modifying the distribution of the inputs to a layer to speed up network learning and prevent vanishing or exploding gradients. Batch normalization normalizes the input to each layer to have a consistent mean and variance and helps the network convergence be easier. Other normalization techniques include:
Layer normalization: Normalizes across each layer.
Instance normalization: Usually used in image processing, it normalizes each instance separately.
Benefits and Challenges of Activation Functions
Activation functions offer several advantages to neural networks, but they also present challenges that need to be addressed. Let's first discuss the benefits of the activation functions.
Non-linearity: The most important benefit of activation functions is that they introduce non-linearity into the network. This helps the networks capture non-linear patterns in data and is ideal for tasks such as image recognition and natural language understanding.
Output range: Activation functions like sigmoid and softmax bound the outputs within a specific range (0-1 for sigmoid and between -1 and 1 for tanh). This makes it much simpler to understand the outputs, especially in classification tasks.
Efficient computation: Some functions, like ReLU, are computationally efficient, which lets networks scale up and be applied to large datasets.
Now, let's discuss the challenges of activation functions.
Vanishing gradient problem: it is common in deep neural networks, mainly when using activation functions like sigmoid and tanh. During backpropagation, the gradients can become very small as they propagate through multiple network layers, causing the slow convergence of the network from learning effectively.
Exploding Gradients: Exploding gradients are a problem in which large error gradients accumulate, resulting in very large updates to the weights of neural network models during the training process. This makes the model unstable and unable to learn from the training data.
Choice of function: Choosing the optimal activation function for a task or neural network can be challenging and usually requires some experimentation. It depends on the type of problem we are trying to solve.
Use Cases of Activation Functions
Activation functions are important components of various neural network architectures that perform different tasks. Here are some key applications:
Image classification: Convolutional Neural Networks (CNNs) use ReLU activation in their hidden layers to process pixel data and softmax in the output layer for multi-class classification.
Natural language processing (NLP): Recurrent Neural Networks (RNNs), Long Short-Term Memory (LSTM), and Transformers use tanh or ReLU activations in their hidden layers to process sequential data.
Generative models: Generative Adversarial Networks (GANs) typically use ReLU or LeakyReLU in the generator network to introduce non-linearity and generate realistic outputs and sigmoid in the discriminator network.
Several deep learning frameworks, including TensorFlow and PyTorch, provide a wide range of built-in activation functions and implementations to create your custom ones.
FAQs about Activation Functions
- What is the activation function?
Activation functions are fundamental building blocks of neural networks that allow them to learn complex patterns in input data. They convert a node's (neuron) input signal into an output signal, which is then passed to the next neural network layer.
- Why is the ReLU activation function used?
The ReLU activation function introduces nonlinearity in a neural network, which helps reduce the vanishing gradient problem during machine learning model training.
- What are the most commonly used activation functions?
ReLU, Leaky ReLU, Softmax, and Swish are popular activation functions.
- What is the activation function used for?
The main purpose of an activation function is to transform the summed weighted input from a node into an output value, which is then passed on to the next hidden layer or used as the final output.
- Can you have multiple activation functions?
Yes, it's common to have different activation functions in different layers of a neural network. For example, a standard configuration might use ReLU activation in hidden layers and softmax in the output layer for a multi-class classification problem.
Further Resources
- What are Activation Functions?
- How Activation Functions Work
- Comparison
- Benefits and Challenges of Activation Functions
- Use Cases of Activation Functions
- FAQs about Activation Functions
- Further Resources
Content
Start Free, Scale Easily
Try the fully-managed vector database built for your GenAI applications.
Try Zilliz Cloud for Free