学習
AIと機械学習

バッチとレイヤーの正規化 - ニューラルネットワークの効率性を引き出す

Mar 22, 20242 分で読めます

レイヤーとバッチの正規化の複雑さを解明することで、ニューラルネットワークの初心者に、効率を引き出し、モデルの性能を向上させるための知識を提供することを目的としています。

シリーズ全体を読む

♪* はじめに**

ディープラーニングやニューラルネットワークが複雑化し規模が大きくなるにつれ、安定的かつ効率的なトレーニングの確保はますます困難になっている。効率的なトレーニングは、バッチ正規化レイヤーとテクニックがこれらの課題の一部を軽減するために介入するところである。正規化によって、ネットワーク層を通過するデータが管理可能な範囲内に留まることが保証される。2015年、「バッチ正規化：Accelerating Deep Network Training by Reducing Internal Covariate Shift"](https://arxiv.org/pdf/1502.03167.pdf)がGoogleからバッチ正規化テクニックを発表した。1年後、トロント大学から "Layer Normalization"](https://arxiv.org/abs/1607.06450)というタイトルの論文がレイヤー正規化に関するテクニックを発表した。

この記事では、これらのテクニックをレビューし、それぞれの特徴的な機能、利点、アプリケーション、Pythonの構文を探ります。レイヤー正規化とバッチ正規化を理解し比較することで、ニューラルネットワークの初心者が効率性を引き出し、モデルのパフォーマンスを向上させるために必要な知識を身につけることを目指す。

正規化](https://assets.zilliz.com/A_close_up_of_a_blueprint_Description_automatically_generated_bdba42d0db.jpg)

正規化**を理解する

**この最適化プロセスは、さまざまなデータ分布の影響を緩和するのに役立つだけでなく、ニューラルネットワークの各層への入力が管理可能な範囲内にあることを保証することによって、学習プロセスを安定させるのにも役立ちます。

正規化が取り組む主な課題のひとつは、内部共変量シフトである。内部共変量シフトとは、各ニューラルネットワークレイヤーに入るデータが、ネットワークが学習するにつれて変化する現象を指します。動いているターゲットに命中させようとすることを想像してみてほしい。同様に、データが変化し続けると、ネットワークが効果的に学習することが難しくなる。正規化することで、データをより安定した状態に保つことができます。

正規化は、入力データの分布に一貫性を持たせることで、内部の共変量シフトを緩和し、よりスムーズで効率的な学習を促します。入力を正規化することで、ニューラルネットワークはより安定した勾配の流れを維持することができ、収束が早くなり、ニューラルネットワークモデルの全体的な効率と精度が向上します。

バッチノルムはどのように機能するのか？

バッチ正規化またはバッチノルムは訓練で広く使われているテクニックで、異なるミニバッチデータ間で各層の入力を正規化する体系的なアプローチを提供します。このプロセスでは、バッチ平均を差し引き、バッチ標準偏差で割ることで、与えられた平均と分散のレイヤーのアクティベーションを正規化します。

そのプロセスと式は以下の通りである：

訓練中、バッチと空間次元を削減することにより、ミニバッチに対応する平均と標準偏差を計算する。各ミニバッチ内の入力を正規化することにより、バッチ正規化ノルムを実装することで、内部の共変量シフトを減らし、学習プロセスを安定させ、収束を早めることができる。このバッチ正規化レイヤーは、特に消失勾配や爆発勾配の問題が発生する可能性のある深いアーキテクチャにおいて、ニューラルネットワークをより効率的かつ効果的に学習することを可能にする。

この正規化プロセスは、各入力テンソルの特徴次元（チャネル）に対して独立して適用される。パラメータγとβは、他のニューラルネットワークパラメータとともに学習中に学習される。

バッチ正規化の利点と欠点

バッチノルムの4つの主要な利点と潜在的な欠点を下表に示す：

|-------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------|------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------| | バッチ・ノルムの利点｜バッチ・ノルムの欠点｜｜バッチ・ノルムの利点 | 内部共変量シフトを減らすことで、訓練中の収束を早める。 | ミニバッチ統計量に依存するため、これらの統計量が利用できない推論では性能が制限される可能性があります。また、シーケンスモデルでは、潜在的に異なる長さのシーケンスを持つ可能性があり、より長いシーケンスに対応する小さいバッチサイズがあるため、シーケンスモデルにはあまり適していません。| | 学習プロセスを安定させ、より高い学習率とモデルの汎化を可能にする。 | バッチ統計量を計算し、活性を正規化する必要があるため、訓練中にさらなる計算オーバーヘッドが発生する。 | | 正則化の効果をもたらし、ドロップアウトなどの他の正則化テクニックの必要性を減らす。| バッチサイズが小さい場合や、入力分布が大きく変動する場合、性能が低下する可能性がある。 | | 勾配の消失や爆発による影響を緩和し、ディープニューラルネットワークの学習を容易にする。 | トレーニング中にノイズが発生し、場合によっては最適でないパフォーマンスや収束の問題につながることがある。 | アーキテクチャと設計の選択に応じて、バッチ正規化はレイヤーの活性化関数の前または後に適用できる。その欠点にもかかわらず、バッチ正規化を適用することは、トレーニングの効率と性能の面で具体的な利点を提供し、ニューラルネットワークの実践者にとって依然として貴重なツールである。

レイヤー正規化とは？

レイヤー正規化またはレイヤー規範はバッチ正規化の代替アプローチを提示する。これは、バッチサイズとは無関係に、各層の特徴間の入力を正規化することに焦点を当てる。データのミニバッチで動作するバッチ正規化とは異なり、レイヤー正規化はデータセット全体にわたって各入力レイヤーの活性を正規化する。

このプロセスでは、各サンプル内の前のレイヤーの特徴間のアクティブ度の平均と標準偏差を計算し、各レイヤー内の入力を効果的に独立に正規化する。これにより、バッチサイズの変動に対してネットワークがロバストであることが保証され、異なるデータセットや入力分布にわたって安定した学習が容易になります。

バッチ正規化と同様に、この（レイヤー）正規化プロセスは、各入力テンソル特徴次元（チャンネル）に対して独立して適用される。レイヤーの正規化は、特徴次元全体の統計量を計算する。

レイヤー正規化の利点と欠点

バッチ正規化の4つの主要な利点と潜在的な欠点を下表に示す：

|-------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------|--------------------------------------------------------------------------------------------------------------------------------------------------------| | レイヤー・ノームの長所｜レイヤー・ノームの短所｜レイヤー・ノームの長所と短所 | 特徴量間で独立にアクティブ度を正規化するため、バッチサイズが小さい、またはバッチサイズが可変のシナリオに適している。 | バッチサイズが大きいシナリオでは、バッチ正規化の方が適している可能性がある。 | | 入力分布やバッチサイズの変化に強く、トレーニング中の安定性が高い。 | バッチ統計量を計算する必要がないため、バッチ正規化と比較して学習時の計算オーバーヘッドが最小。 | | バッチ正規化のような正則化効果があり、モデルの汎化を向上させる。 | 特にバッチサイズが大きく、単純なネットワーク・アーキテクチャの場合、バッチ正規化よりも収束が遅くなることがある。| | リカレント・ニューラル・ネットワーク](https://zilliz.com/glossary/recurrent-neural-networks)(RNN)や、入力シーケンスの長さが異なるトランスフォーマーベースのモデルにも適用可能。| 正規化スケールやシフト・パラメータ（ガンマやベータ）などのハイパーパラメータを調整する必要がある。 | 層の正規化は、隠れ層の前の層のアーキテクチャと設計の選択に応じて、層の活性化関数の前または後に適用することができる。

バッチ正規化とレイヤー正規化の比較

レイヤー正規化とバッチ正規化はニューラルネットワークの学習プロセスを安定させ加速させる強力なツールです。しかし、これらは異なる原理で動作し、明確な特徴を示すため、特定のアプリケーションでどちらかを選択する際には注意深く考慮する必要があります。下の表は、レイヤー正規化とバッチ正規化について説明した比較分析です。


ファクター**	レイヤー規範	バッチ規範
正規化アプローチ**｜特徴量全体（レイヤごと）の活性度を正規化する。	ミニバッチ全体（レイヤごと）の活性を正規化する。
計算**｜特徴間の統計量を計算する。	ミニバッチ間の統計量を計算する。
バッチサイズに依存しない。	安定したトレーニングのためには十分に大きなバッチサイズが必要。
オンラインまたはリアルタイムの推論に適している。	バッチ依存性のため推論に追加調整が必要な場合がある。
入力シーケンスの長さが変化する可能性があるリカレントニューラルネットワーク (RNNs)やトランスフォーマベースのモデルに適している。	フィードフォワード・ニューラル・ネットワークや畳み込みニューラルネットワーク(CNN)でよく使われ、特にバッチサイズが大きく一定している場合に効果的である。
特に大きなバッチサイズと単純なネットワークアーキテクチャーでは、バッチ正規化に比べて収束が遅くなる場合があります。	バッチ統計量を計算し、活性を正規化する必要があるため、トレーニング中に追加の計算オーバーヘッドが発生します。
使用例**｜ ▶リカレントニューラルネットワーク(RNN)-トランスフォーマーベースのモデル- オンラインまたはリアルタイムの推論シナリオ｜ ▶フィードフォワードニューラルネットワーク-畳み込みニューラルネットワーク(CNN)- バッチサイズが大きく、一貫性のあるシナリオ｜ ▶レイヤーの正規化とバッチサイズの選択

レイヤー正規化とバッチ正規化のどちらを選択するかは、データセット固有の特性、ニューラルネットワークのアーキテクチャ、トレーニング環境の計算制約など、さまざまな要因によって決まります。バッチ正規化はトレーニングダイナミクスの安定化と収束の促進に優れていますが、レイヤー正規化は、特にバッチサイズが小さいシナリオやデータ分布が変動するシナリオにおいて、より高い柔軟性とロバスト性を提供します。

バッチ正規化とレイヤー正規化の使用例

レイヤー規範とバッチ規範は様々な領域で広く応用されており、ニューラルネットワークの訓練と性能を強化する上で有効であることが実証されています。ここでは、これらの正規化技術が効果的に実装された実際のアプリケーションとシナリオを掘り下げる：

画像処理：**物体検出や画像分類のようなコンピュータビジョンのタスクにおいて、レイヤノルムとバッチノルムは学習ダイナミクスを安定させ、モデルの汎化を改善する上で重要な役割を果たす。これらの技術は、データのばらつきの影響を緩和し、照明条件、視点、物体のスケールのばらつきに対するニューラルネットワークモデルの頑健性を高めるのに役立つ。
自然言語処理(NLP): 言語モデリング、機械翻訳、センチメント分析などのNLPタスクでは、正規化は、文の長さ、単語の分布、言語的ニュアンスが異なるという課題に対処するのに役立ちます。レイヤーノルムとバッチノルムは学習プロセスを安定化させるのに役立ち、ニューラルネットワークモデルが長距離依存関係を捕捉し、多様なテキストデータセットで優れた性能を達成することを可能にする。
強化学習：** ゲームプレイやロボット工学などの強化学習アプリケーションでは、正規化は学習プロセスを安定化させ、ポリシーの収束を加速させる上で極めて重要である。ポリシーパラメータ、レイヤノルム、バッチ正規化に対する一貫性のある安定した更新を保証することで、より効率的な探索と利用戦略が容易になり、学習効率とタスク性能の向上につながります。
画像やテキスト生成のような生成モデリングタスクでは、正規化は学習プロセスの安定性と収束を保証するために不可欠です。レイヤノルムとバッチ正規化は、モード崩壊を緩和し、生成されたサンプルの多様性と品質を向上させ、より現実的で首尾一貫した出力につながります。

これらの多様なアプリケーションとユースケースを探索することで、我々は様々なドメインとタスクにおけるレイヤーとバッチ正規化の汎用性と有効性について貴重な洞察を得ることができる。次のセクションでは、ニューラルネットワーク内のバッチ正規化パラメータとテクニックの新たなトレンドについて説明し、この進化する分野の将来を垣間見ます。次のセクションでは、画像認識のためのPythonプログラミング言語におけるバッチ正規化とレイヤー正規化の実践的なハンズオン例を見ていきます。

Pythonでのバッチ正規化-例

必要な依存関係をすべてインポートすることから始めます：

# 必要なパッケージをインポートする
np として numpy をインポートする
import matplotlib.pyplot as plt
import tensorflow as tf
from tensorflow.keras.datasets import mnist
from tensorflow.keras.models import シーケンシャル
from tensorflow.keras.layers import Dense, Flatten, BatchNormalization
from tensorflow.keras.optimizers import Adam

以降、MNISTデータセットをロードし、データを前処理する：

# MNIST データセットをロードする。
(X_train, y_train), (X_test, y_test) = mnist.load_data()
X_train, X_test = X_train / 255.0, X_test / 255.0.

次に、バッチノルムを使わない単純なニューラルネットワークモデル（model_no_bn）を次のように定義する：

# バッチノルムのないシンプルなニューラルネットワークモデルを定義する
model_no_bn = シーケンシャル([
    Flatten(input_shape=(28, 28))、
    Dense(128, activation='relu')、
    Dense(64, activation='relu')、
    Dense(10, activation='softmax')
])

その後、バッチノルムを使わずにモデルをコンパイルして訓練する：

# バッチノルムなしのモデルをコンパイルして訓練する
model_no_bn.compile(optimizer='adam'、
                    loss='sparse_categorical_crossentropy'、
                    メトリクス=['accuracy'])
history_no_bn = model_no_bn.fit(X_train, y_train, epochs=5, validation_data=(X_test, y_test), verbose=2)

バッチノルムを用いた単純なニューラルネットワークモデルを定義します（model_with_bn）：

# バッチノルムを用いた単純なニューラルネットワークモデルを定義する。
model_with_bn = シーケンシャル([
    Flatten(input_shape=(28, 28))、
    Dense(128, activation='relu')、
    バッチ正規化()、
    Dense(64, activation='relu')、
    バッチ正規化()、
    Dense(10, activation='softmax')
])

バッチノルムでモデルをコンパイルし、訓練する：

# バッチノルムを用いたモデルのコンパイルと学習
model_with_bn.compile(optimizer='adam'、
                      loss='sparse_categorical_crossentropy'、
                      メトリクス=['accuracy'])
history_with_bn = model_with_bn.fit(X_train, y_train, epochs=5, validation_data=(X_test, y_test), verbose=2)

最後に、両モデルの学習カーブを可視化し、性能を比較する。

# 学習曲線を可視化する
plt.figure(figsize=(10, 5))
plt.subplot(1, 2, 1)
plt.plot(history_no_bn.history['accuracy'], label='トレーニング精度（BNなし）')
plt.plot(history_no_bn.history['val_accuracy'], label='検証精度（BNなし）')
plt.xlabel('Epoch')
plt.ylabel('精度')
plt.title('バッチ正規化なしのトレーニング曲線')
plt.legend()

plt.subplot(1, 2, 2)
plt.plot(history_with_bn.history['accuracy'], label='トレーニング精度（BNあり）')
plt.plot(history_with_bn.history['val_accuracy'], label='検証精度（BNあり）')
plt.xlabel('Epoch')
plt.ylabel('精度')
plt.title('Training Curves with Batch Normalization')
plt.legend()

plt.tight_layout()
plt.show()

上に示したコードのスクリプト全体の出力は、以下のようになります（実行するたびにグラフが異なることに注意してください）：

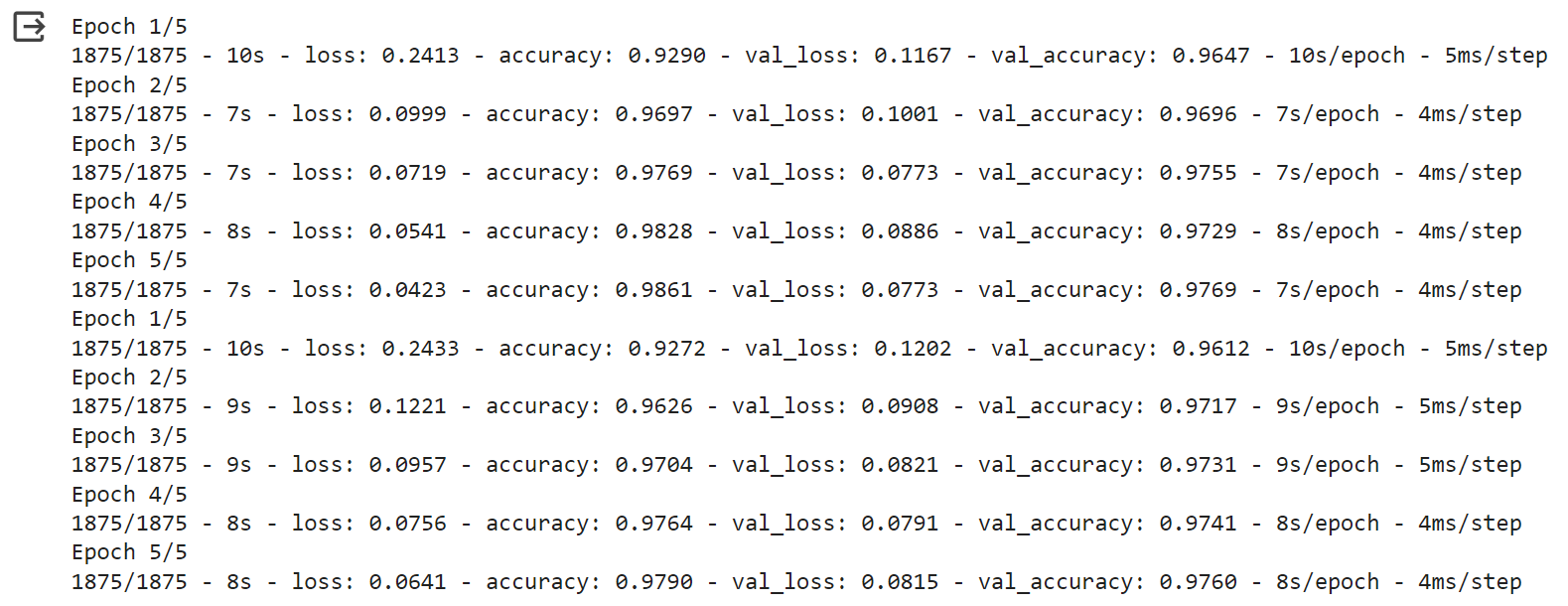
出力の解読

トレーニングログは、トレーニングセットと検証セットの両方について、トレーニングプロセス中の各エポックにおけるテストデータに対する損失と精度の値を示している。

結果の解釈:

損失と精度の傾向:** 損失の値を見ると、モデルが予測において改善していることを示す、エポックにわたって損失が減少することを目指します。また、精度の値は、トレーニングデータセットと検証データセットの両方において、より良いパフォーマンスを反映し、上昇することを望みます。
より速い収束：*** バッチ正規化モデルは、より速く****収束するようです。"収束"とは、モデルの性能が安定する、またはプラトーに達する時点を指します。この文脈では、モデルがデータ中のパターンをより速く学習し、学習プロセスにおいてより早く高い精度を達成することを意味します。
学習率：「学習率」という用語は通常、最適化アルゴリズムにおけるハイパーパラメーターを指しますが、ここでは、モデルが学習データから学習する速度として非公式に理解することができます。収束が速いほど、有効学習率が高いことを意味することが多く、これはモデルが損失を最小化するために、より速くパラメータを更新することを意味する。

要約すると、バッチノルムを用いたモデルは、バッチノルムを用いないモデルと比較して、より速い学習を示し、より少ないエポックでより良い性能（より高い精度）を達成する。これはバッチノルムが学習プロセスの安定化と高速化に有効であることを示している。

Pythonにおけるレイヤーの正規化-例

必要な依存関係を全てインポートすることから始める：

# 必要な依存関係をインポートする
np として numpy をインポートする。
import matplotlib.pyplot as plt
import tensorflow as tf
from tensorflow.keras.datasets import mnist
from tensorflow.keras.models import シーケンシャル
from tensorflow.keras.layers import Dense, Flatten, LayerNormalization
from tensorflow.keras.optimizers import Adam

その後、MNISTデータセットをロードし、データを前処理する：

# MNIST データセットをロードする。
(X_train, y_train), (X_test, y_test) = mnist.load_data()
X_train, X_test = X_train / 255.0, X_test / 255.0.

次に、レイヤーの正規化を行わない単純なニューラルネットワークモデル（model_no_ln）を次のように定義する：

# レイヤーの正規化を行わないシンプルなニューラルネットワークモデルを定義する。
model_no_ln = シーケンシャル([
    Flatten(input_shape=(28, 28))、
    Dense(128, activation='relu')、
    Dense(64, activation='relu')、
    Dense(10, activation='softmax')
])

その後、レイヤーの正規化を行わずにモデルをコンパイルし、学習する：

# レイヤー正規化なしのモデルをコンパイルする。
model_no_ln.compile(optimizer='adam'、
                    loss='sparse_categorical_crossentropy'、
                    metrics=['accuracy'])

# レイヤー正規化なしでモデルをトレーニングする
history_no_ln = model_no_ln.fit(X_train, y_train, epochs=5, validation_data=(X_test, y_test), verbose=2)

レイヤーの正規化（model_with_ln）を伴う単純なニューラルネットワークモデルを定義します：

# レイヤー正規化を使ったシンプルなニューラルネットワークモデルを定義する
model_with_ln = シーケンシャル([
    Flatten(input_shape=(28, 28))、
    Dense(128, activation='relu')、
    LayerNormalization(), # レイヤー正規化レイヤーの追加
    Dense(64, activation='relu')、
    LayerNormalization(), # レイヤー正規化レイヤーの追加
    Dense(10, activation='softmax')
])

バッチノルムでモデルをコンパイルし、訓練する：

# レイヤ正規化を使ってモデルをコンパイルする
model_with_ln.compile(optimizer='adam'、
                      loss='sparse_categorical_crossentropy'、
                      metrics=['accuracy'])

# レイヤー正規化を使ってモデルをトレーニングする
history_with_ln = model_with_ln.fit(X_train, y_train, epochs=5, validation_data=(X_test, y_test), verbose=2)

最後に、両モデルの学習曲線を可視化し、性能を比較する。

# 学習曲線を可視化する
plt.figure(figsize=(10, 5))

# レイヤーの正規化を行わずに学習曲線をプロットする
plt.subplot(1, 2, 1)
plt.plot(history_no_ln.history['accuracy'], label='学習精度（LNなし）', color='blue')
plt.plot(history_no_ln.history['val_accuracy'], label='検証精度（LNなし）', color='orange')
plt.xlabel('Epoch')
plt.ylabel('Accuracy')
plt.title('層正規化なしのトレーニング曲線')
plt.legend()

# レイヤー正規化を行った学習曲線をプロットする
plt.subplot(1, 2, 2)
plt.plot(history_with_ln.history['accuracy'], label='学習精度（LNあり）', color='blue')
plt.plot(history_with_ln.history['val_accuracy'], label='検証精度（LNあり）', color='orange')
plt.xlabel('Epoch')
plt.ylabel('Accuracy')
plt.title('Training Curves with Layer Normalization')
plt.legend()

plt.tight_layout()
plt.show()

上記のコードのスクリプト全体の出力は以下のようになる（実行するたびにグラフが異なることに注意）：

出力の解読

この出力は、MNISTデータセットを5エポック学習した、レイヤー正規化なしとレイヤー正規化ありの2つのモデルの学習進捗を示している。

レイヤー正規化なしモデルの場合：*。

当初、学習精度は92.93%、検証精度は96.09%であった。
5エポックの学習後、学習精度は約98.68%まで上昇し、検証精度は約97.38%に達する。
全体的に、レイヤー正規化を行わないモデルは、エポック数を重ねるごとに、訓練精度と検証精度が着実に向上しています。

レイヤー正規化ありのモデルの場合:。

同様に、このモデルは約93.61%の訓練精度と約96.70%の検証精度でスタートします。
5エポック後、学習精度は約98.70%まで向上しますが、検証精度は3エポック目で約96.58%まで落ち込み、その後約97.76%まで再び向上します。
3回目のエポック後に検証精度が一時的に落ち込んだにもかかわらず、レイヤー正規化を行ったモデルは、レイヤー正規化を行わなかったモデルよりも高い検証精度を達成しています。

まとめると、どちらのモデルもエポックを重ねるごとに学習精度と検証精度が向上している。しかし、レイヤー正規化を行ったモデルは、トレーニング中に検証精度が一時的に低下するものの、同等かそれよりもわずかに優れた性能を示している。これは、トレーニング中の分散を安定させ、時間の経過とともにモデルの性能を向上させるレイヤー正規化の有効性を強調するものである。

バッチ正規化とレイヤー正規化の今後の方向性とベストプラクティス

ニューラルネットワークトレーニングの分野が進化し続ける中、正規化技術は研究と革新の最前線にあります。ニューラルネットワークにおける正規化の最も顕著な新興トレンドと将来の方向性は以下の通りです：

1.適応型正規化：有望な方向性の1つは、データの特性とトレーニングダイナミクスに基づいて、トレーニング中に動的にパラメータを調整する適応型正規化の開発です。適応的正規化法は、様々な入力分布や学習環境に対するニューラルネットワークモデルの頑健性と適応性を高めることを目的としている。

2.**各層のチャンネルをグループに分け、各グループ内の正規化統計量を独立に計算します。グループ正規化は、バッチ正規化やレイヤ正規化に代わるアプローチを提供し、特に計算資源が限られているシナリオにおいて、柔軟性と効率性を向上させます。

3.**リカレントニューラルネットワーク（RNN）やトランスフォーマーベースモデルなど、特定のニューラルネットワークアーキテクチャに合わせた技術も注目されている。カスタマイズされた正規化レイヤーと戦略は、これらのアーキテクチャ特有の課題と要件に対処するのに役立ち、性能と効率をさらに高めることができます。

4.正規化を正則化のフレームワークに組み込むことで、実務家はモデルの複雑性をよりよく制御し、オーバーフィッティングを防ぐことができます。

ベストプラクティスという点では、ニューラルネットワーク分野の初心者は、さまざまな正規化テクニックを試し、多様なデータセットとタスクでそのパフォーマンスを評価することが推奨される。各正規化手法に関連するトレードオフと考慮事項を理解することは、モデル設計とトレーニングにおいて十分な情報に基づいた意思決定を行う上で極めて重要である。

結論

このブログでは、ディープラーニングのニューラルネットワークトレーニングの領域における2つのテクニックであるレイヤー正規化とバッチ正規化の概念についてレビューしました。それぞれの特徴的な機能、利点、アプリケーション、実践的な実例を探ることで、モデルの効率とパフォーマンスを向上させる上での役割について貴重な洞察を得ることができた。

レイヤー正規化とバッチ正規化は、内部共変量シフトの課題に対処し、学習プロセスを安定化させるための補完的なアプローチを提供する。バッチ正規化がトレーニングダイナミクスの安定化と収束の促進に優れているのに対し、レイヤー正規化は、特にバッチサイズが小さい場合やデータ分布が変動するシナリオにおいて、より高い柔軟性とロバスト性を提供します。

これらの長所と短所を理解することで、実務者はモデル設計とトレーニングにおいて十分な情報に基づいた意思決定を行うことができ、最終的に、より効率的で効果的なニューラルネットワークアーキテクチャを導き出すことができる。

結論として、レイヤーの正規化とバッチの正規化は、ニューラルネットワークの実践者にとって不可欠なツールである。これらは、トレーニングダイナミクスの安定化、モデル性能の向上、自然言語処理とコンピュータビジョンタスクの実行、ニューラルネットワークアーキテクチャの効率化のための強力なメカニズムを提供する。Zillizチームは、様々な機械学習プロジェクトにおいて、これらのテクニックのさらなる探求と実験を奨励し、この分野の継続的な進歩への道を開く。

さらなるリソース

article.updateAt