Prover-Verifier Games Improve Legibility of LLM Outputs
We discussed the checkability training approach to help LLMs generate accurate answers that humans can easily understand and verify.
Read the entire series
- OpenAI's ChatGPT
- Unlocking the Secrets of GPT-4.0 and Large Language Models
- Top LLMs of 2024: Only the Worthy
- Large Language Models and Search
- Introduction to the Falcon 180B Large Language Model (LLM)
- OpenAI Whisper: Transforming Speech-to-Text with Advanced AI
- Exploring OpenAI CLIP: The Future of Multi-Modal AI Learning
- What are Private LLMs? Running Large Language Models Privately - privateGPT and Beyond
- LLM-Eval: A Streamlined Approach to Evaluating LLM Conversations
- Mastering Cohere's Reranker for Enhanced AI Performance
- Efficient Memory Management for Large Language Model Serving with PagedAttention
- LoRA Explained: Low-Rank Adaptation for Fine-Tuning LLMs
- Knowledge Distillation: Transferring Knowledge from Large, Computationally Expensive LLMs to Smaller Ones Without Sacrificing Validity
- RouteLLM: An Open-Source Framework for Navigating Cost-Quality Trade-Offs in LLM Deployment
- Prover-Verifier Games Improve Legibility of LLM Outputs
- Be like a Goldfish, Don't Memorize! Mitigating Memorization in Generative LLMs
- Unlocking the Power of Many-Shot In-Context Learning in LLMs
- Spotting LLMs With Binoculars: Zero-Shot Detection of Machine-Generated Text
- Teaching LLMs to Rank Better: The Power of Fine-Grained Relevance Scoring
It's no secret that one of the main goals behind the development of large language models (LLMs) is to help humans solve complex problems. To achieve this goal, LLMs are often trained on various data to optimize their problem-solving skills across domains, such as math, coding, and general question-answering tasks. To measure an LLM's performance, we assess its correctness in answering various tasks during training and testing.
The assumption is that the more data we have and the longer we train an LLM, the more capable it will become, therefore, the better its correctness will also be. However, correctness alone is not enough for an LLM to be helpful to humans. We also need to pay attention to its legibility, i.e., whether we as humans can easily understand and verify the answers from the LLM. We need to easily understand the LLM's responses to ensure that we can trust its answers.
To address this issue, we need to train or fine-tune an LLM to provide correct and easy-to-understand answers. In this article, we'll discuss a training method inspired by the Prover-Verifier Game theory to achieve both capable and easy-to-understand LLMs. So, let's get started!
The Fundamental of Prover-Verifier Games Theory
Having an LLM capable of generating correct answers on various tasks is not enough, particularly if it intends to be helpful to humans. Its answers should also be understandable so that humans can verify their validity.
However, experimental results have shown that training an LLM solely to optimize its correctness can make its answers harder for humans to understand. Human evaluators made twice as many errors when asked to evaluate the answers from optimized models compared to less-optimized models in a time-constrained situation. Therefore, it's necessary to train LLMs not only to generate correct answers but also easy-to-understand ones, i.e., to be more legible to humans.
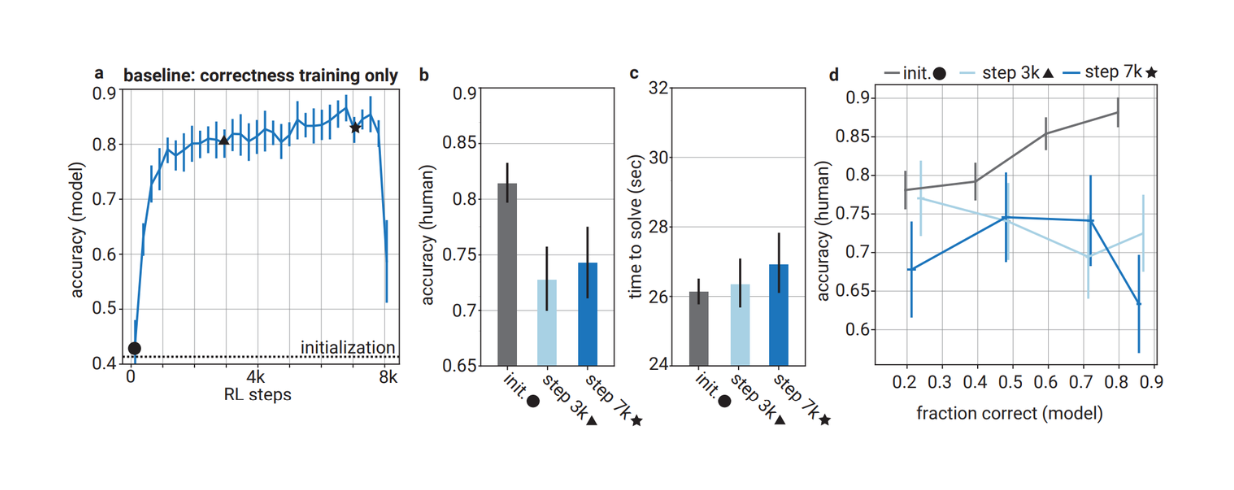Comparison between the accuracy of the model optimized solely based on correctness vs. the accuracy of human evaluators when evaluating their answers
Comparison between the accuracy of the model optimized solely based on correctness vs. the accuracy of human evaluators when evaluating their answers. Source.
To achieve this goal, an iterative algorithm called checkability training has been proposed. This method is inspired by the Prover-Verifier Game, a game theory framework that encourages agents to solve problems understandably. This framework has two main components: the prover and the verifier.
In a nutshell, the prover generates an answer to a given query, and the verifier checks the correctness of the answer generated by the prover. We can think of the prover as the LLM and the verifier as the human.
To substitute for a human, the verifier is represented by a smaller, less capable model than the prover. However, both the prover and verifier are from the same model family. Choosing a smaller, less capable LLM as the verifier serves at least two purposes:
LLMs have proven to be more scalable and capable of judging LLMs' outputs compared to humans.
Human feedback is limited for such an advanced system, especially when the domain requires subject expertise. Therefore, making the answer verifiable by a smaller, less capable model would eventually also help make it more verifiable to humans.
Example of a correct answer from the model with poor legibility
Example of a correct answer from the model with poor legibility. Source.
Checkability Training Setup
To make LLM output more legible to humans, the prover and verifier are trained one after another for several rounds in a checkability training framework. In each round, the verifier is first trained on a specific mixture of data with supervised learning to predict the correctness of answers. Next, the prover is trained with reinforcement learning, with the reward being a combination of the answers' correctness and the current round verifier's acceptance rate.
During the prover model's training, we divide it into two roles: helpful and sneaky. The helpful prover tries to generate correct solutions to problems, while the sneaky prover tries to generate 'convincing' incorrect solutions. Therefore, during the reinforcement learning training, the helpful prover will be rewarded for being correct and convincing, while the sneaky prover will be rewarded for being incorrect and convincing.
The main goal of checkability training is to optimize two metrics: completeness and soundness.
Completeness: For any query, the helpful prover generates a correct answer, which the verifier accepts as correct.
Soundness: For any query, the verifier can reject incorrect but convincing answers generated by the sneaky prover.
Therefore, the perfect result after checkability training would be for the verifier to have a high recall rate on helpful answers (good completeness) and a low false positive rate on incorrect answers from the sneaky prover (good soundness).
As mentioned in the previous section, the checkability training runs for several rounds. In each round, the verifier is trained first before we train the prover model. In this training implementation, there are two important things we should pay attention to:
The only difference between one round and another is the data mixture. The weights of both verifier and prover models from the previous round are not carried over to the next round.
Both verifier and prover should come from the same model family, such as the GPT-4 family. This can be helpful in answering questions like: "Can one system trust another system of a particular size, architecture, trained with a particular algorithm?"
The GSM dataset, which contains a set of problems and their ground-truth answers, is used for the checkability training. Given a proposed solution from the prover model, the correctness label would be one if it's similar to the ground-truth answer and 0 otherwise.
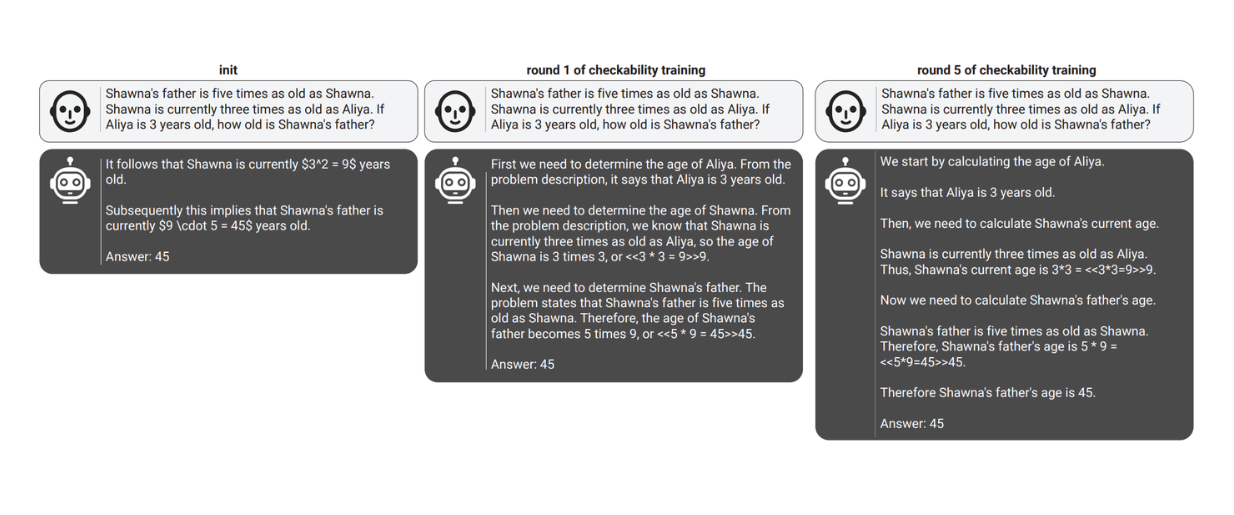Example of prover responses on the same prompt across different training rounds
Example of prover responses on the same prompt across different training rounds. Source.
In each round, the verifier is trained with supervised learning based on a random subset of the data and optimized with standard gradient descent. Next, the prover model is trained with reinforcement learning, where the policy is conditioned on either the helpful or sneaky role with equal probability.
The reward of the prover is then a combination of both roles: if the prover role is helpful and generates more correct answers, the higher the reward it will get. Likewise, if the prover role is sneaky and generates more convincing incorrect answers, the higher the reward it will get. Also, regardless of the role, the prover will get a higher reward when the verifier gives a higher score to the solution proposed by the prover. This reward function is called Signed Relative Convincingness (SRC).
Aside from SRC, there are two other variants of rewards experimented with during the checkability training:
Correctness-Gated Convincingness (CGC): This reward function prioritizes role-alignment more. For example, the reward will be higher if the helpful prover generates more correct answers and the sneaky prover generates more incorrect answers.
Iterative Goodharting: This reward function prioritizes convincingness more. The prover will get a higher reward when the verifier gives a higher score to the solution proposed by the prover.
Checkability Training Results with SRC Reward Function
Both verifiers and provers are trained over five rounds with the three variants of reward functions mentioned above. The first one to test is the training dynamics with the SRC reward.
In each of the five rounds, helpful and sneaky provers can improve their convincingness to the verifier as the training progresses. Meanwhile, the portion of correct answers generated by the helpful prover in each round changes non-monotonically over training steps.
The sneaky prover generates correct answers at the beginning of the steps in each round before starting to generate incorrect answers that convince the verifier. The training in each round is stopped as soon as the incorrect answers generated by the sneaky prover are as convincing as the correct answers generated by the helpful prover. However, as you can see in the visualization below, as the training rounds increase, the sneaky prover struggles more to produce incorrect, convincing solutions.
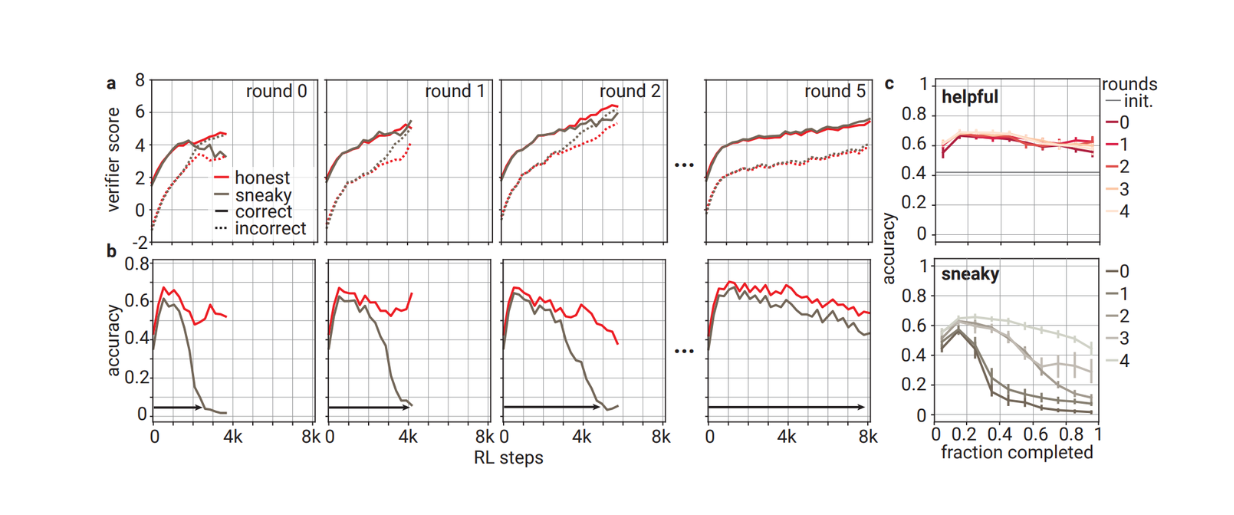Dynamics of checkability training using SRC reward function
Dynamics of checkability training using SRC reward function. Source.
The more advanced the training round, the more steps are needed to stop the training process, as the sneaky prover needs longer to generate incorrect solutions that convince the verifier. However, the root cause of this phenomenon is unclear, and it might be caused by the weight sharing between helpful and sneaky provers during checkability training. Therefore, checkability training was conducted using three reward functions between the sneaky-only prover and various verifiers with different sizes.
During each training round with SRC and CGC reward functions, the training is stopped as soon as the sneaky prover generates 95% incorrect answers, and the average verifier score on incorrect answers becomes as high as that of the helpful prover's correct answers. Meanwhile, for the goodharting reward function, the training is stopped as soon as optimizing a prover on the verifier score reaches an accuracy of < 0.2.
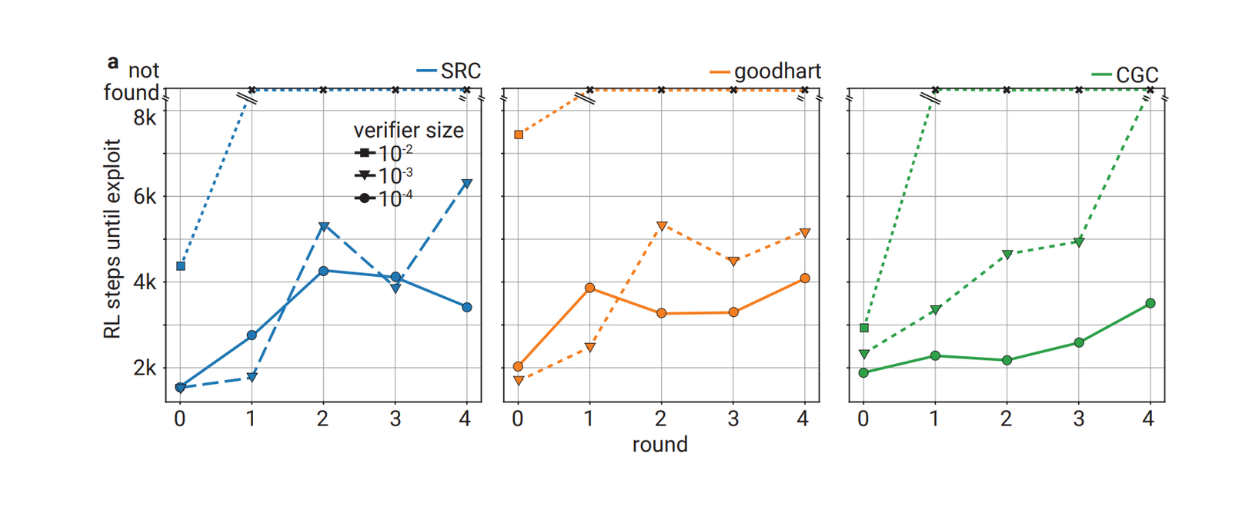Robustness of several verifiers with different model sizes against incorrect solutions provided by the sneaky-only prover
Robustness of several verifiers with different model sizes against incorrect solutions provided by the sneaky-only prover. Source.
The results show a similar trend to what we've seen before. In general, the further we are in the training rounds, the more steps it takes for the sneaky prover to be able to exploit the verifier. Also, as you can see, the larger the size of the verifier model, the harder it is for the sneaky prover to exploit it.
The verifier with a relative size of 10-2 compared to the prover is more difficult to exploit than the other two smaller verifiers. In fact, the verifier with a relative size of 10-2 remains unexploitable from round 1 until the last round of checkability training with 8k reinforcement learning steps. Meanwhile, the verifier with a relative size of 10-3 remains exploitable when training with SRC and goodharting reward functions. Nonetheless, this experiment has shown that the verifier gets more and more robust against incorrect solutions throughout checkability training.
Now that we know the verifier's behavior, let's shift our attention to the sneaky prover, especially the quality of its generated answers throughout the checkability training. The experiment has shown that the incorrect solutions generated by the sneaky prover become increasingly subtle the further we are in the training rounds. This phenomenon can be seen below in the GPT-4 validity score and the human accuracy score.
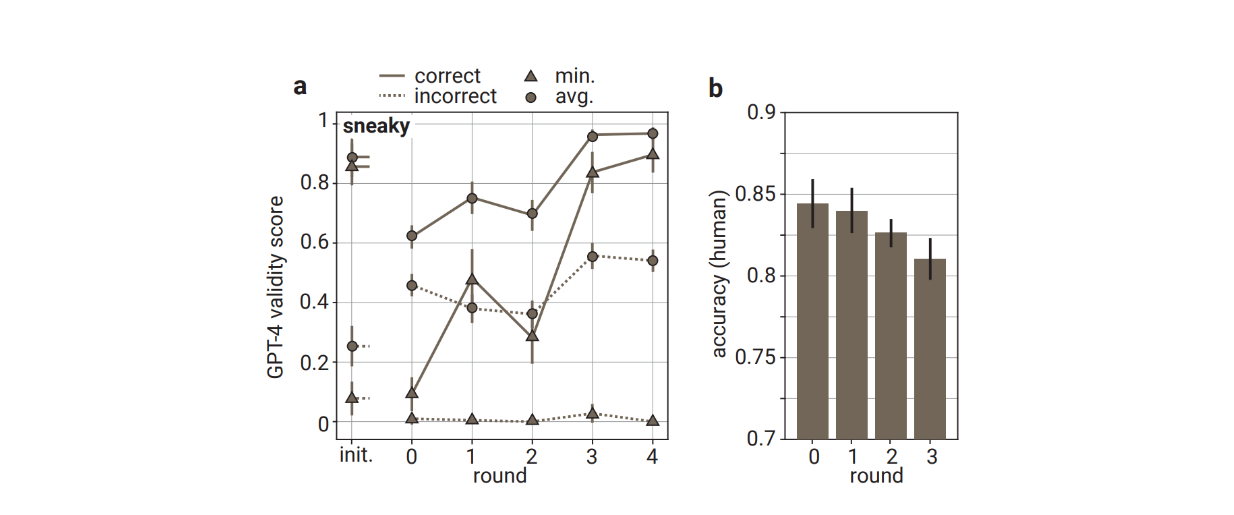Validity score from GPT-4 and the accuracy of human evaluators on answers provided by sneaky prover across different training rounds
Validity score from GPT-4 and the accuracy of human evaluators on answers provided by sneaky prover across different training rounds. Source.
The average validity score generated by GPT-4 on solutions generated by the sneaky prover increases across different training rounds. Also, when human contractors are presented with answers from the sneaky prover across different rounds, their assessment accuracy decreases the further we are in the training rounds. This tells us that the incorrect answers generated by the sneaky prover get more and more subtle throughout checkability training.
Example of how the incorrect solutions provided by sneaky provers become more subtle as the checkability training progresses
Example of how the incorrect solutions provided by sneaky provers become more subtle as the checkability training progresses. Source.
Next, let's discuss the helpful prover. Throughout the checkability training, the helpful prover's accuracy or correctness increases across different rounds. However, as mentioned in the previous section, the main goal of this experiment is to check not only the solution's correctness but also its legibility to human evaluators.
To check this, human evaluators were asked to assess the solutions generated by the helpful prover model in each training round. The result suggests that while the correctness is improving, the solution's legibility is also improving.
As you can see in the visualization below, the accuracy of human evaluators in evaluating the solutions generated by the helpful prover increases over each training round. Not only that, but the time it takes for human evaluators to check the solution becomes shorter, indicating that the solution generated by the helpful prover becomes more legible to humans.
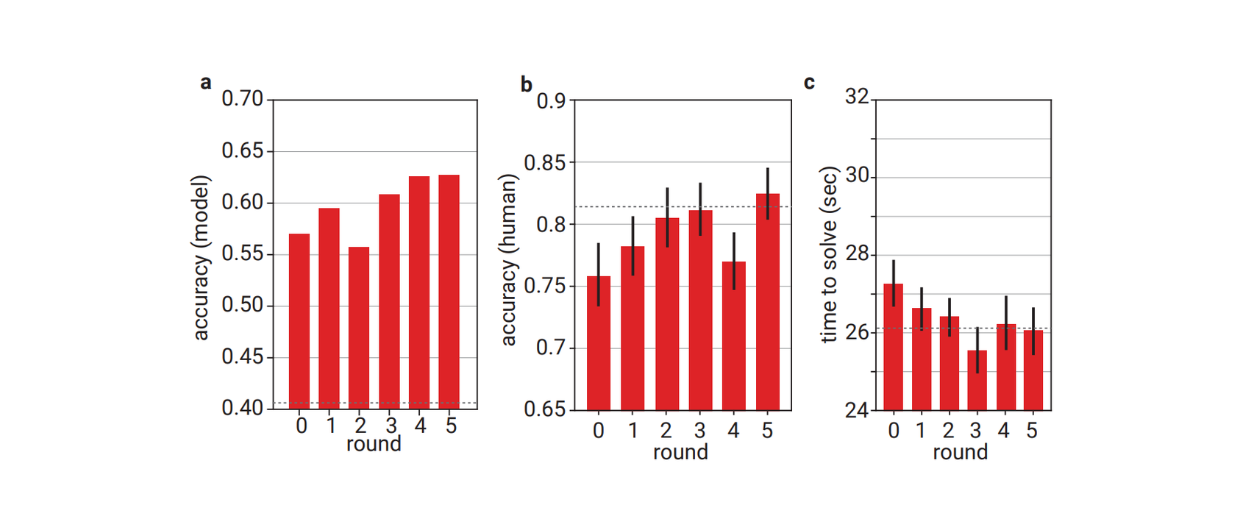The correctness of the model and the accuracy of human evaluators improve as checkability training progresses
The correctness of the model and the accuracy of human evaluators improve as checkability training progresses. Source.
However, the accuracy of the helpful model trained on both correctness and legibility is noticeably lower than the model trained only on correctness. This shows that in order to improve the legibility of the answer, we need to sacrifice a certain percentage of correctness accuracy.
Checkability Training Results with Other Reward Functions
So far, we've seen the results of checkability training using the SRC reward function. Next, let's examine the training results using the other two reward functions mentioned in the previous section: CGC and Iterative Goodharting.
CGC is a reward function that prioritizes correctness over convincingness. Therefore, the reward is a constant penalty when the helpful prover produces an incorrect solution or the sneaky prover produces a correct solution. If they're correct, the reward is the verifier score.
Overall, the training dynamics using CGC are worse compared to SRC. As you can see in the visualization below, the number of RL steps the sneaky prover takes until it successfully convinces the verifier does not increase consistently across different training rounds. Due to these worse training dynamics, no human evaluations were performed for training using the CGC reward.
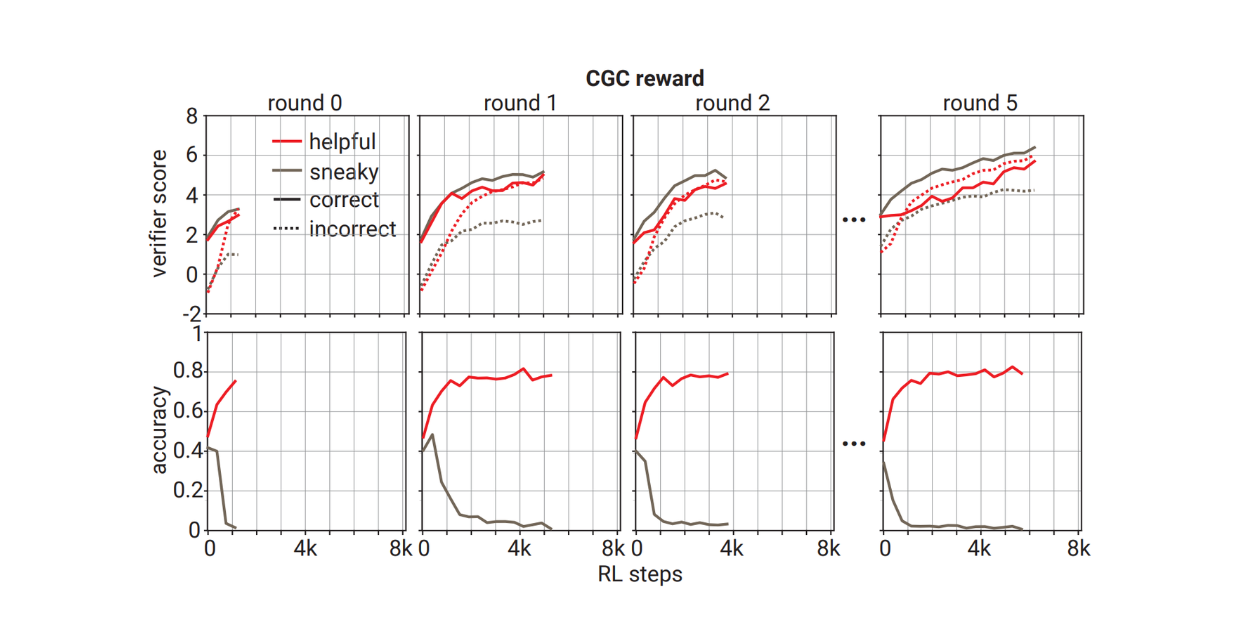The dynamics of checkability training using CGC reward function
The dynamics of checkability training using CGC reward function. Source.
Another reward function aside from CGC is iterative good charting. This reward function doesn't have an assigned role, meaning the reward comes completely from the verifier score. Therefore, it focuses more on convincingness rather than correctness.
Based on its training dynamics, the prover takes more steps to over-optimize the solution across training rounds. From the experimentation results, verifiers of medium sizes (about 3x10-3 relative to the prover model) benefit the most from checkability training using this iterative good charting reward function compared to smaller or larger verifiers.
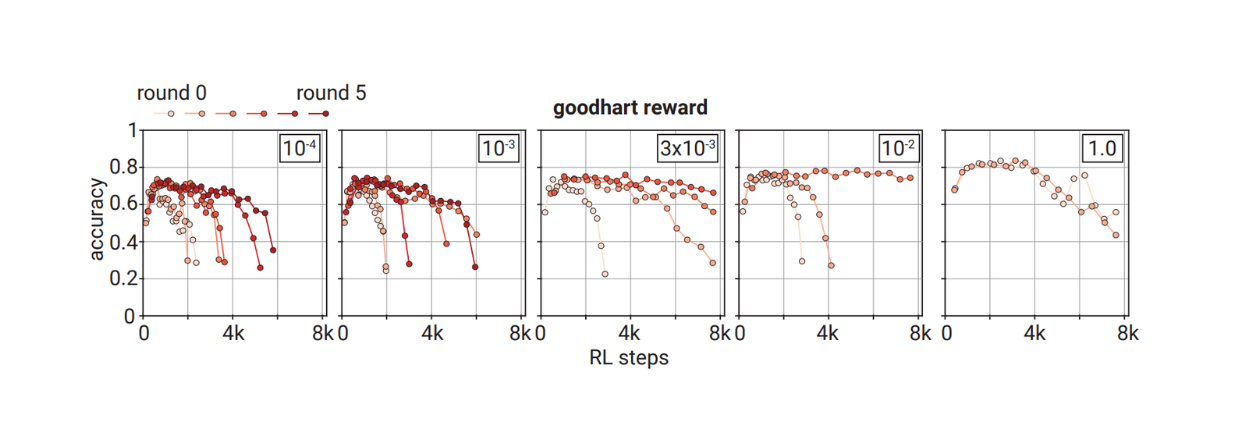The dynamics of checkability training using iterative goodharting reward function
The dynamics of checkability training using iterative goodharting reward function. Source.
However, when the answers after iterative goodharting training are presented to human evaluators, there is no noticeable difference in human evaluator accuracy across different training rounds. This indicates that the checkability training using this reward function doesn't really improve legibility.
Checkability Training Limitations and Future Work
In the previous sections, we saw that checkability training helps to improve an LLM's correctness and legibility to humans. However, several limitations can be addressed in the current implementation of checkability training.
The training setup necessitates a ground-truth label for every question to check the correctness of the model. For example, the GSM dataset, which contains simple and standardized solutions, is used for checkability training.
However, finding datasets with standardized labels is quite difficult in real life, while collecting ground-truth answers can be time-consuming and cost-consuming. Therefore, one possible future work is extending checkability training to an unsupervised setup.
Also, the current checkability training relies on problems with hard 'correct-incorrect' answers, such as math or coding problems. If we train the model on data that involves ambiguities or human preferences, it becomes difficult to quantify its performance. Further experimentations with heterogeneous set-ups (i.e., no early stopping within RL steps) and hyperparameter tuning would be beneficial to see their impacts on the model's final correctness and legibility.
Conclusion
In this article, we've discussed all aspects of checkability training inspired by the Prover-Verifier Game theory. This training approach offers a methodical way to train LLMs to provide accurate answers and ensure these answers are understandable and verifiable by humans. The experimental results show that this approach improves the correctness and legibility of helpful provers while making sneaky provers' incorrect solutions increasingly subtle yet detectable by robust verifiers.
Despite its advancements, checkability training has several limitations, such as its reliance on datasets with standardized ground-truth labels and the challenge of scaling to ambiguous or subjective problem domains. Addressing these challenges will be important for the more general applicability of this method.
Related Resources
- The Fundamental of Prover-Verifier Games Theory
- Checkability Training Setup
- Checkability Training Results with SRC Reward Function
- Checkability Training Results with Other Reward Functions
- Checkability Training Limitations and Future Work
- Conclusion
- Related Resources
Content
Start Free, Scale Easily
Try the fully-managed vector database built for your GenAI applications.
Try Zilliz Cloud for Free