Learn
Embedding 101

What Are Binary Embeddings?

May 30, 202413 min read

In this blog, we will introduce the concept of binary embeddings, delineating their defining characteristics, advantages, and comparative merits against other embedding types.

By Denis Kuria

Read the entire series

Introduction

Vector embeddings have become indispensable in modern machine learning and data science, facilitating the representation of complex data in a numerical format comprehensible to algorithms. While dense embeddings are prevalent for their ability to retain semantic meaning with minimal information loss, their computational demands and memory requirements escalate as data volumes soar. This escalation prompts developers to seek more efficient data representation methods.

Amidst the array of techniques, binary embeddings have emerged as a compelling solution, striking a balance between compactness, computational efficiency, and meaningful data representation. In this blog, we will introduce the concept of binary embeddings, delineating their defining characteristics, advantages, and comparative merits against other embedding types. Additionally, we will delve into methods for generating binary embeddings and illustrate the implementation of binary embedding search using the Milvus vector database.

What Are Vector Embeddings?

Before covering binary embeddings, it's essential to establish a foundational understanding of vector embeddings.

Vector embeddings are numerical representations of discrete data items, encompassing entities like words, sentences, images, or other elements. Each item is mapped to a vector comprising real numbers within a high-dimensional space. Similar items gravitate closer together within this space, while dissimilar ones diverge.

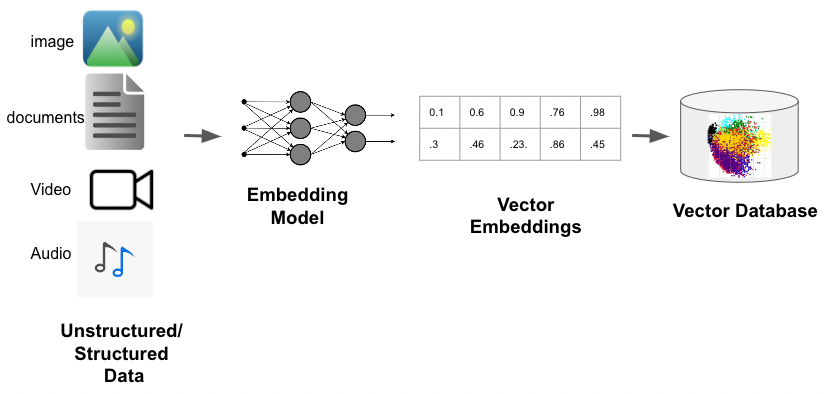How vector embeddings are generated and stored

How vector embeddings are generated and stored

The potency of vector embeddings manifests prominently in their capacity to encapsulate semantic relationships between items. For instance, in natural language processing (NLP), words with akin meanings or contextual relevance are portrayed by vectors positioned closely within the vector space, thus facilitating nuanced analysis and interpretation.

Vector embeddings are usually stored in specialized vector databases such as Milvus and Zilliz Cloud (the fully managed Milvus).

What are Binary Embeddings?

Binary embeddings are a type of vector representation in which each dimension is encoded using a single binary digit, typically represented as either 0 or 1. For instance, a binary word embedding for "cat" could be represented as [0, 1, 0, 1, 1, 0, 0, 1, ...], where each dimension is binary.

Binary embeddings offer storage efficiency and computational speed. Since they use only one bit per dimension, they require less memory than other types of embeddings, making them suitable for applications with limited memory resources or large datasets. Additionally, operations involving binary values are often faster to execute than operations involving real-valued numbers.

Despite their efficiency, binary embeddings may sacrifice some accuracy compared to dense embeddings, which contain real-valued entries in most or all dimensions. This is because binary embeddings represent data in a simplified binary format, which may not capture all the nuances or complexities in the original data.

Dense vs. Sparse vs. Binary Vector Embeddings

Vector embeddings exhibit different characteristics based on their dimensionality. Let's dissect the distinctions among dense, sparse, and binary embeddings:

Dense embeddings comprise vectors with real-valued, non-zero entries in most or all dimensions, offering high accuracy but necessitating more storage and computation than binary or sparse embeddings. For instance, a dense image embedding might appear as [0.2, -0.7, 1.1, 0.4, -0.3, 0.9, -0.1, ...], where most or all dimensions have non-zero real values.
Sparse embeddings consist of vectors with numerous zero values, making them memory-efficient but potentially computationally expensive for certain operations. For example, a sparse sentence embedding could manifest as [0, 0, 2.5, 0, 0, -1.2, 0, 0, 0, 3.7, ...], where most dimensions are zero.
In binary embeddings, each vector dimension is represented by a single bit (0 or 1), offering storage efficiency and computational advantages. However, they may compromise some accuracy compared to dense embeddings.

In these examples, the differences among binary (0 or 1), sparse (mostly 0s), and dense (real-valued) embeddings are apparent. Selecting an appropriate embedding type hinges on the trade-off between accuracy, storage, and computation required for the specific application.

How to Generate Binary Embeddings

There are several main approaches to generating binary embeddings: Hash-based methods, machine learning models, and Binary Quantization.

Hashing-based methods

Hashing-based methods utilize locality-sensitive hashing (LSH) or random projections to directly map high-dimensional input data to binary codes. LSH generates binary codes by partitioning the input space into hash buckets and assigning binary codes to each bucket. Random projections map input data to lower-dimensional spaces using random projection matrices, with subsequent quantization to obtain binary codes.

Machine Learning Models

Deep learning architectures, such as deep belief networks (DBNs) and restricted Boltzmann machines (RBMs), generate binary embeddings as part of their output. RBMs, in particular, can learn binary representations in their hidden layers by applying stochastic binary activations. Binary Neural Networks, which use binary activations and weights during training and inference, are another option for generating binary embeddings.

Binary Quantization

Quantization-based techniques convert continuous-valued embeddings into binary representations. Vector quantization methods like k-means clustering can learn codebooks, where each centroid represents a binary code. Input data is then quantized by assigning it to the nearest centroid, yielding binary representations. Binary quantization is particularly useful when memory or computational resources are limited, such as embedded systems or large-scale machine learning models.

What is Binary Quantization?

Binary quantization is a technique that transforms dense or sparse embeddings into binary representations by thresholding each vector dimension to either 0 or 1 as shown in the diagram below.

How binary quantization works.

How binary quantization works.

All positive numbers are marked as 1; otherwise, they become 0.

This process can be achieved through various quantization methods, such as simple sign thresholding, scalar quantization, or more complex techniques like vector quantization. Let us see how to conduct binary quantization using simple sign thresholding.

Conducting Binary Quantization

We get started by installing the required libraries:

!pip install sentence_transformers scikit-learn

The sentence-transformers package provides a pre-trained model for generating sentence embeddings. Scikit-learn contains the Binarizer class which you'll use for binary quantization.

Then import the above libraries to your code to use their supported classes and modules.

from sentence_transformers import SentenceTransformer
from sklearn.preprocessing import Binarizer

Proceed to load one of the pre-trained models to generate high-quality sentence embeddings. The all-MiniLM-L6-v2 model is lightweight and pre-trained on a large corpus of text data. This is the model you will use to generate dense vector embeddings.

from sentence_transformers import SentenceTransformer
from sklearn.preprocessing import Binarizer

Then, use the loaded model's encode method to generate dense embeddings for our input document. The encode method takes a list of strings (in this case, a single document) and returns a list of Numpy arrays, where each array represents the dense embedding for the corresponding input string.

# Document to embed
document = ("Why Zilliz Cloud? Zilliz Cloud provides a fully-managed Milvus service, "
           "made by the creators of Milvus. It simplifies the deploying and scaling "
           "of vector search applications by eliminating the need to construct "
           "and maintain complex infrastructure.")


# Generate dense embeddings
dense_embeddings = model.encode([document])

Since you have generated dense embeddings of your document, the next step is conducting binary quantization and printing the results.

# Binary quantization using scikit-learn Binarizer
binarizer = Binarizer(threshold=0.0)
binary_embeddings = binarizer.transform(dense_embeddings)


print("Dense Embeddings (first 10 dimensions):")
print(dense_embeddings[0][:10])
print("\nBinary Embeddings (first 10 dimensions):")
print(binary_embeddings[0, :10])

The above code performs binary quantization on the dense embeddings to obtain binary embeddings. It starts by creating an instance of the Binarizer class from sci-kit-learn, with a threshold of 0.0. Any positive value in the dense embeddings will be converted to 1, and any negative value will be converted to 0.

It then uses the transform method of the Binarizer instance to perform the binary quantization on the dense embeddings. Here is a screenshot of the results obtained from running the above code:

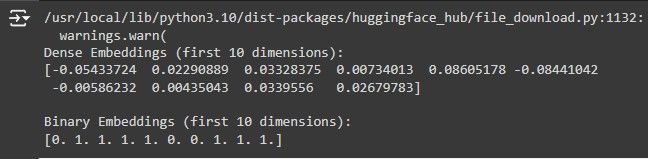
The dense embeddings with corresponding binary embeddings are obtained via binary quantization in the screenshot. Let us now see how to conduct a binary embedding search.

How Does Milvus Conduct a Binary Embedding Search?

Milvus is an open-source vector database for efficiently storing and retrieving vector embeddings. Milvus efficiently supports binary embedding search through two primary indexes: BIN_FLAT and BIN_IVF_FLAT. Let's see how each index performs a binary embedding search.

Milvus's Binary Indexes

BIN_FLAT: The BIN_FLAT index is a straightforward approach suitable for relatively small datasets where a 100% recall rate is essential. It performs an exhaustive search by comparing the query vector with every vector in the dataset, ensuring exact search results. However, this exhaustive approach can be computationally expensive and slow for large datasets, making it less practical for massive-scale applications.
BIN_IVF_FLAT: The BIN_IVF_FLAT index balances search speed and recall rate. It employs a quantization-based approach, dividing the vector data into multiple cluster units (nlist). During a search, it compares the query vector with the centroid of each cluster and selects the most similar clusters (nprobe) for further comparison with individual vectors within those clusters. This technique significantly reduces the search time by limiting the comparisons to a subset of the dataset while maintaining a high recall rate.

To better understand how to perform binary embedding searches with Milvus, let's implement a practical example:

Performing Binary Embedding Searches With Milvus

To perform a binary embedding search in Milvus, you need to encode your documents to their representation of dense vector embeddings. Then, you can perform binary quantization and store and retrieve the embeddings related to a query from Milvus.

Here is a step-by-step guide for conducting a binary embedding search with Milvus.

Step 1: Setting Up Your Environment

Before you begin coding, you should have Milvus installed on your computer and the required library to connect to Milvus installed. To install and run Milvus, follow this comprehensive guide. Then, proceed to the terminal and run the following command to install the required library.

! pip install pymilvus[model]

This command will install Pymilvus, a library enabling you to connect with the Milvus instance running on your computer. It will also install milvus-model, giving you access to all the embedding models supported by Milvus. After the library, import the necessary modules and classes to your code.

from pymilvus import MilvusClient, DataType
from pymilvus.model.hybrid import BGEM3EmbeddingFunction
import numpy as np

You will use MilvusClient to connect to your Milvus instance and DataType to define the collection fields' data types. As for the BGEM3EmbeddingFunction, you will use it to represent your documents in dense vector embeddings. The BGE-M3 model is chosen in this guide as it is Multilingual; hence, you can use it to embed over 100 languages.

Step 2: Defining a Function to Convert Dense Vectors to Binary Vectors

This function will help us perform binary quantization. It will convert embeddings generated by BGEM3EmbeddingFunction from their dense (Numpy arrays) format to binary.

# Function to convert dense vector to binary vector
def dense_to_binary(dense_vector):
   return np.packbits(np.where(dense_vector >= 0, 1, 0))

This function takes a dense vector as input and converts it to a binary vector using NumPy's packbits function. The packbits function packs the binary values (represented as 1s and 0s) into bytes, which can be efficiently stored and retrieved in Milvus.

Step 3: Instantiating the Pre-trained Sentence Embedding Model

Next, instantiate the pre-trained multilingual sentence embedding model from the pymilvus.model.hybrid module:

bge_m3_encoder = BGEM3EmbeddingFunction(
   model_name='BAAI/bge-m3', device='cpu', use_fp16=False
)

You will use this model to generate dense embeddings for your documents and queries. These embeddings will then be converted to binary format using the dense_to_binary function.

Step 4: Connecting to Milvus Instance

Now connect to the Milvus instance using the MilvusClient class:

client = MilvusClient(
   uri="http://localhost:19530"
)

Replace the uri with the appropriate connection details for your Milvus instance.

Step 5: Defining the Collection Schema

Next, define the schema for your Milvus collection. This schema will store your documents and their corresponding binary embeddings:

schema = MilvusClient.create_schema(
   auto_id=True,
   enable_dynamic_field=True,
)

# Add fields to schema
schema.add_field(field_name="doc_id", datatype=DataType.INT64, is_primary=True)
schema.add_field(field_name="doc_text", datatype=DataType.VARCHAR, max_length=65535)
schema.add_field(field_name="doc_binary_embedding", datatype=DataType.BINARY_VECTOR, dim=1024)

Here is what field in the above schema represents:

doc_id: A unique identifier for each document (primary key).
doc_text: The textual content of the document.
doc_binary_embedding: The binary embedding of the document, which will be used for similarity search.

Step 6: Creating or Dropping the Collection

Since you have a schema, the next step is to create a collection with it. But first, check whether a similar collection exists, and if it does, you drop it.

collection_name = "binary_embedding_collection"

# Drop the existing collection if it exists
if client.has_collection(collection_name):
   client.drop_collection(collection_name)

# Create the collection
client.create_collection(
   collection_name=collection_name,
   schema=schema,
   description="Binary Embeddings collection"
)

Since you created a collection with a certain schema, you will have to pass data that matches this schema to the collection later. Else, a mismatch error will arise.

Step 7: Creating the Search Index

To enable efficient similarity search, proceed to create an index on the doc_binary_embedding field:

# Create index parameters
index_params = [{
   "field_name": "doc_binary_embedding",
   "index_type": "BIN_IVF_FLAT",
   "metric_type": "JACCARD",
   "params": {"nlist": 128}
}]

client.create_index(collection_name, index_params)
print("New index created successfully.")

The above code uses the BIN_IVF_FLAT index we discussed earlier and the JACCARD metric. These are suitable for binary embeddings in Milvus. Jaccard Metric measures the similarity between binary vectors. It calculates the ratio of the number of bits that are 1 in both vectors compared to the total number of bits.

Step 8: Inserting Your Documents

Since you have created a collection and defined the indexing method, you can insert some documents into your collection:

# Documents to insert
documents = [
   "Zilliz is a high-performance data science company focused on data science and analytics. It provides advanced optimization and rapid deployment, enabling the solution of scientific and technical problems.",
   "Milvus is an open-source software project that is emerging in the market of vector databases. It is an extremely effective and simple solution in the field of data science and machine learning, which makes it possible to efficiently process data for various use cases. Milvus is developed specifically for processing data for vector similarity and approximate queries in a fast and simple manner."
]

# Insert documents into the collection
for doc_text in documents:
   doc_embedding = bge_m3_encoder.encode_documents([doc_text])['dense'][0]
   binary_embedding = dense_to_binary(doc_embedding)
   entity = {
       "doc_text": doc_text,
       "doc_binary_embedding": binary_embedding.tobytes()
   }
   insert_result = client.insert(collection_name, [entity])
   print(f"Inserted document: {doc_text[:20]}...")

For each document in the documents list, the code:

Generates a dense embedding using the pre-trained bge_m3_encoder model.
Converts the dense embedding to a binary embedding using the dense_to_binary function.
Creates an entity dictionary containing the document text and binary embedding.
Insert the entity into the Milvus collection using the client.insert method.

Step 9: Performing Similarity Search on Collection

Since you have successfully inserted your documents and their corresponding binary embeddings into Milvus, you must perform a similarity search to retrieve related documents to a query.

Start by loading the created collection into memory.

client.load_collection(collection_name)

Then, define the search parameters for the similarity search.

search_params = {
   "metric_type": "JACCARD",
   "params": {"nprobe": 10}
}

Setting the nprobe parameter to 10 means that during a query, the search algorithm will examine the top 10 clusters most likely to contain the nearest neighbors to the query vector. This reduces the computational load and speeds up the search process.

Finally, proceed to perform a similarity search to a sample query:

query_text = "What is Milvus?"
query_embedding = bge_m3_encoder.encode_queries([query_text])['dense'][0]
binary_query_embedding = dense_to_binary(query_embedding)

# Perform similarity search
search_result = client.search(
   collection_name=collection_name,
   data=[binary_query_embedding.tobytes()],
   limit=10,
   output_fields=["doc_text", "doc_binary_embedding"],
   search_params=search_params
)

The above code does the following:

Take a query text: "What is Milvus?".
Generates a dense embedding for the query using the bge_m3_encoder model.
Then, it converts the dense embedding to a binary embedding using the dense_to_binary function.
Finally, it performs the similarity search using the client.search method, passing in the binary query embedding, the collection name, and the search parameters.

Step 10: Printing the Results

This is the final step to performing the binary embedding search with Milvus. It involves printing the results returned by Milvus as a result of the similarity search:

# Print the first hit
if search_result and len(search_result[0]) > 0:
   first_hit = search_result[0][0]
   entity = first_hit['entity']
   print(f"Answer: {entity['doc_text']}")
  
   # Print binary embeddings
   query_binary_str = ''.join(format(byte, '08b') for byte in binary_query_embedding.tobytes())
   print(f"Query Binary Embedding: {query_binary_str}")
  
   first_hit_binary_str = ''.join(format(byte, '08b') for byte in np.frombuffer(entity['doc_binary_embedding'], dtype=np.uint8))
   print(f"First Hit Binary Embedding: {first_hit_binary_str}")
else:
   print("No results found.")

The above code block checks if the search result is not empty and contains at least one hit (a similar document). If the search result is not empty and has at least one hit, it extracts the first hit, which is the most similar document to the query.

It then prints the text of the most similar document, which is the answer to the query, as it is the document whose binary embedding is closest to the binary embedding of the query. After printing the document text, it generates binary string representations of the query's binary embedding and the binary embedding of the first hit using list comprehensions and the format function.

Here is a screenshot of the results obtained from conducting a similarity check on the query: What is Milvus?

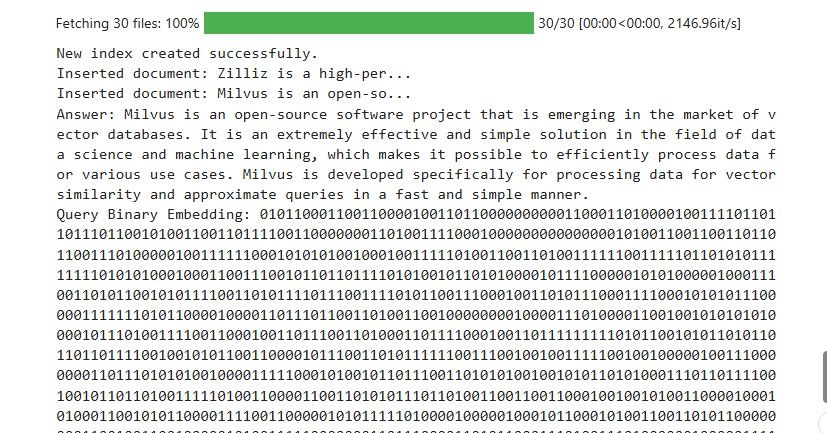results.jpg

The screenshot above shows that the document retrieved from Milvus is correct for our query.

Stay tuned for future releases of Milvus, which will incorporate binary quantization capabilities. This addition will empower you to leverage binary embeddings' benefits directly within the Milvus ecosystem.

Conclusion

In this guide, you have explored the concept of binary embeddings, contrasting them with dense and sparse embeddings and highlighting their advantages in terms of storage efficiency and computational speed. You learned about different approaches to generating binary embeddings and how binary embeddings can be leveraged for efficient similarity search using Milvus.

By understanding their characteristics and implementation methods, you can effectively harness binary embeddings' power to tackle real-world machine learning and data science challenges.

Further Resources

Denis Kuria
Denis is a machine learning engineer who enjoys writing guides to help other developers. He has a bachelor's in computer science and loves hiking and exploring the world.

Next: A Beginner's Guide to Website Chunking and Embedding for Your RAG Applications