ベクトル量子化のパワーを解き放つ：効率的なデータ圧縮と検索のテクニック
ベクトル量子化(VQ)は、データ圧縮技術の一つで、セントロイドと呼ばれる、より小さな代表ベクトルの集合で、類似したデータ点の大きな集合を表現する。
シリーズ全体を読む
- BGE-M3とSplade: スパース埋め込みを生成する2つの機械学習モデルの探究
- SPLADEスパース・ベクターとBM25の比較
- ColBERTの探求：効率的な類似検索のためのトークン・レベルの埋め込みとランキング・モデル
- UnstructuredとMilvusによるEPUBコンテンツのベクトル化とクエリ
- バイナリ・エンベッディングとは？
- RAGアプリケーションのためのウェブサイト・チャンキングと埋め込み入門ガイド
- ベクトル埋め込み入門：ベクトル埋め込みとは何か？
- 画像検索のための画像埋め込み：詳細な説明
- OpenAIのテキスト埋め込みモデルを使うための初心者ガイド
- DistilBERT：BERTの蒸留バージョン
- ベクトル量子化のパワーを解き放つ：効率的なデータ圧縮と検索のテクニック
#はじめに
今日のデータ駆動型の世界では、膨大なデータセット、特に様々なAIアプリケーションで使用されるvector embeddingsのような高次元データの管理は、ストレージ、計算、転送、検索に大きな課題をもたらしている。データ圧縮は、実用性を犠牲にすることなく情報サイズを縮小し、より高速な処理と費用対効果の高いストレージを可能にする重要な戦略となっています。
この分野で非常に有用であることが証明されている圧縮技術の1つが、ベクトル量子化（VQ）である。その中核となるベクトル量子化は、高次元空間で類似したデータ点をクラスタ化し、各クラスタをセントロイドベクトルで表現する。このアプローチは、重要な特徴を保持しながらデータサイズを大幅に削減するため、画像圧縮、音声処理、機械学習などのアプリケーションに最適です。このブログでは、ベクトル量子化の原理とテクニック、そして最新のAI駆動型システムでよりスマートなデータ圧縮と効率的な検索を可能にする方法についてご紹介します。
データ型
ベクトル量子化を理解するためには、まず様々なデータ型の基本を把握することが重要である。
浮動小数点数は計算における実数を表し、様々な精度で広範囲の値を表現することができます。これらの数値はビットを使って格納されますが、ビットは主に3つの要素に分けられます：符号（正負を表す）、指数（数値をスケーリングする）、仮数または指示数（実際の桁数を表す）。量子化の際にこれらの値を近似することで、VQは本質的な特徴を保持したままデータを効果的に圧縮します。
符号**：符号ビットは数値が正か負かを表します。これは1ビットで、0が正、1が負を表します。
指数：指数：指数は数値のスケールを決定し、小数点以下をシフトすることで 幅広い値を表現できるようにします。この柔軟性により、非常に大きな数値も非常に小さな数値も表現することができる。
仮数（シグニフィカンド）： 仮数部は浮動小数点数の精度部分です。仮数部（シグニフィカンド）：仮数部は浮動小数点数の精度部であり、数値の有効桁（小数部）を含み、実際の値を表します。
例えば、Float32（またはFP32）データ型（図1参照）は32ビットまたは4バイトで表されます（1バイト=8ビットなので）。これは単精度浮動小数点としても知られています。この形式は高い精度を提供しますが、特に大きなデータセットや高次元のベクトルを扱う場合、計算コストが高くなり、かなりの量のメモリを必要とします。
図1 - 標準浮動小数点表現（FP32）.png](https://assets.zilliz.com/Figure_1_Standard_floating_point_representation_FP_32_596efeca0d.png)
図1：標準的な浮動小数点表現（FP32）_Figure 1 - Standard floating-point representation (FP32).png
この表現では、広い範囲の値を扱うことができます。しかし、データの次元が大きくなるにつれて（例えば、Milvusベクトルデータベースに格納され検索される高次元のembeddings）、メモリと計算コストが大きくなります。図2は、FP32とベクトルでよく使われる他の2つのデータ型を比較して、必要なメモリを示したものです：FP16（16 ビット）と INT8（8 ビット）である。
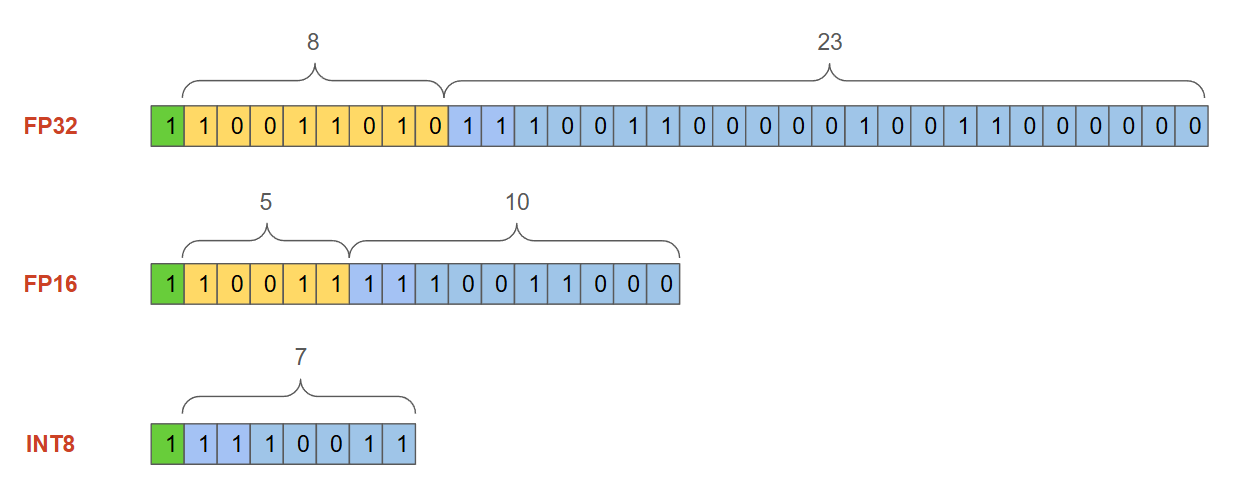図2 - 数値フォーマットの比較.png
図2：数字フォーマットの比較
512次元**のベクトルがあると仮定すると、それを格納するのに必要なメモリは以下の式で計算できる：
方程式](https://assets.zilliz.com/equation_23b1bf8030.png)
| データ型｜ビット｜512次元ベクトル用メモリー｜512次元ベクトル用メモリー | --------- | ------- | --------------------------------- | ------ | | FP32｜32ビット｜2,048バイト｜2キロバイト｜2キロバイト | FP16、16ビット、1,024バイト、1KB | INT8 8ビット 512バイト 0.5キロバイト
図3：512次元ベクトルのメモリ要件
しかし、ビット幅を小さくする（例えば、FP32からINT8へ）と、ある程度の精度が犠牲になるため、メモリ効率と精度の間にはトレードオフがあります。一方、規模を拡大し、何千、何百万ものベクトルを保存するようになると、各ベクトルの精度を完全に維持することは計算コストが高くなり、現実的ではなくなります。このようなシナリオでは、メモリ使用量と精度のバランスが必要になります。そこでベクトル量子化（VQ）が、これらの高次元データポイントのサイズを縮小する強力なデータ圧縮技術として登場します。
ベクトル量子化を理解する
ベクトル量子化(VQ)は、コードワードまたはセントロイドとして知られる、より小さな代表的なベクトルの集合で、類似したデータ点(入力ベクトル)の大規模なセットを表すデータ圧縮技術です。この過程で、入力ベクトルはクラスタ（またはボロノイ領域）にグループ化され、それぞれに代表となるコードワードが割り当てられる。データを表現するために使われるすべてのコードワードの集合をコードブックと呼ぶ。
図4 - ベクトル量子化ダイアグラム](https://assets.zilliz.com/Figure_4_Vector_Quantization_Diagram_5423f8b9ce.png)
図4：ベクトル量子化ダイアグラム
図4は、ベクトル量子化がどのように実行されているかを示す図である。この概念をMilvusのようなベクトルデータベースの文脈で説明するために、自然言語処理モデルからの単語埋め込みなどの高次元ベクトルの膨大なコレクションがあるとします。ベクトルデータベース](https://zilliz.com/learn/what-is-vector-database)のインデックスを構築する際、元のベクトルを使うのではなく、VQを使って最も代表的なベクトル（セントロイド）を特定し、それだけを使うことで、メモリを大幅に節約することができます。これらの量子化されたベクトルによってインデックスが構築され、より高速な検索とretrievalが可能になります。
次に、高次元ベクトルの集合から256のクラスタを作成し、それらを32ビットから16ビット精度に量子化するシナリオをシミュレートしてみましょう。各ベクトルは、256個のコードワード（クラスタ）からなるコードブック内のインデックスに置き換えられ、量子化されたベクトル・インデックスとコードブックの両方のメモリが計算されます。このシナリオでは、メモリ・フットプリントがほぼ75%削減される。
npとしてnumpyをインポート
# 高次元ベクトルのサンプルを生成する
num_vectors = 1000
vector_dim = 1024
# 量子化なし
bits32 = 32 # 32ビット浮動小数点
non_quantized_size = num_vectors * vector_dim * (bits32 / 8) / 1024 # KB単位
print(f "非量子化ベクトルに必要なメモリ: {non_quantized_size:.2f} KB")
# 量子化の詳細
num_clusters = 256 # コードブック内のクラスタ数（コードブックサイズ）
# 量子化されたベクトルインデックス (uint16) とコードブックが使用するメモリ (セントロイド1次元あたり4バイト)
bits16 = 16 # 16ビットインデックス
quantized_indices_16 = num_vectors * (bits16 / 8) # バイト数
codebook_memory_16 = num_clusters * vector_dim * 4 # 各コードワードは4バイト (float32 centroids)
# 量子化メモリの合計（KB
quantized_size_16 = (quantized_indices_16 + codebook_memory_16) / 1024 # KB単位
print(f "16ビット量子化ベクトルに必要なメモリ: {quantized_size_16:.2f} KB")
# 16ビット量子化で節約できるメモリを計算する
savings_16 = (non_quantized_size - quantized_size_16) / non_quantized_size * 100
print(f "16ビット量子化によるメモリ節約: {savings_16:.2f}%")
"""
出力する：
非量子化ベクトルに必要なメモリー：4000.00 KB
16ビット量子化ベクトルに必要なメモリー：1025.95 KB
16ビット量子化によるメモリ節約74.35%
"""
ベクトル量子化の主要テクニック
ベクトル量子化について理解したところで、Zilliz CloudやMilvusのようなベクトルデータベースで使われる一般的なテクニックについて、さらに深く掘り下げてみよう。
スカラー量子化
スカラー量子化**は、浮動小数点数を整数に変換する、最も単純で簡単なものです。一般的に、ほとんどの埋め込みモデルはfloat32データ型を出力し、Zilliz CloudやMilvusのようなベクトルデータベースは、量子化を行う際にそれらをint8整数に変換することができます。int8データ型は8ビットを使用し、範囲は-128から127で、これは元の浮動小数点値がこの範囲内の整数にマッピングされることを意味します。
| --------- | ------- | :------------:| :-----------:| | FP32｜32ビット｜-2'147'483'648｜2'147'483'647 | FP16｜16ビット｜-32'768｜32'767｜｜INT8｜8ビット | INT8｜8ビット｜-128｜127
図5：INT8の範囲
変換は、元データの最小値と最大値に基づく正規化によって行われる。int8にスケールダウンすることで、Zilliz CloudやMilvusのようなデータベースは大幅なメモリ節約を達成することができ、ディスク、CPU、GPUのメモリ消費量を70～75%削減することができる。
図6 - スカラー量子化.png](https://assets.zilliz.com/Figure_6_Scalar_Quantization_6543ea66c3.png)
図6：スカラー量子化
例えば、設定によっては、Milvus IVF_SQ8のスカラー量子化インデックスは、非量子化インデックスと比較して、最大99%の想起率を達成することができ、絶対精度よりもスピードとストレージが優先される大規模システムにとって非常に効率的です。
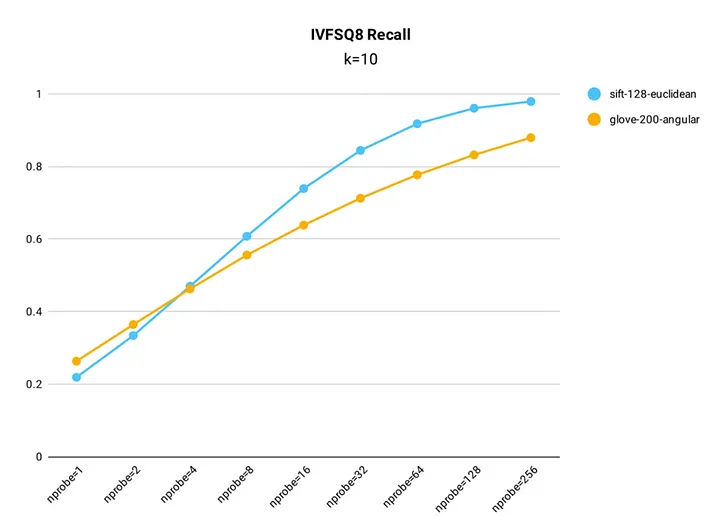図7 - MilvusにおけるIVF_SQ8インデックスの再現率テスト結果.png
図7：MilvusにおけるIVF_SQ8インデックスの再現率テスト結果(Source)_。
積量子化(PQ)
積量子化(PQ)は、スカラー量子化よりも高度な圧縮技術である。PQは、各次元を個別に変換する代わりに、元の高次元ベクトルを、より小さい、等しい長さの部分ベクトルの集合に分割する。この分割により、アルゴリズムはより小さなデータセグメントを扱うことができるようになり、特に高次元空間では圧縮がより管理しやすく効果的になる。
ベクトルがサブベクトルに分割されると、K-meansクラスタリングアルゴリズムが各サブベクトル群（サブスペース）に適用される。クラスタリング](https://zilliz.com/glossary/clustering)を通して、セントロイド（または "コードワード"）のセットが各サブスペースに対して定義され、その独自のコードブックが生成される。そして、各サブベクトルはその最も近いセントロイドにマップされる。このプロセスはすべての部分ベクトルにわたって繰り返され、PQはベクトル全体を各部分空間からの複数のセントロイドの組み合わせとして表現することができる。
その結果、圧縮された表現は、各グループの最も近いセントロイドを参照するインデックスのシーケンスとなり、メモリ使用量が大幅に削減される。例えば図8では、FP32型1024次元（1ベクトルあたり4096バイト）の元のベクトルに対して、ベクトルを256個の部分ベクトルに分割し、各セントロイドIDを8ビット（1バイト）で表現すると、量子化されたベクトルは256バイトで済み、圧縮率は16（4096/256）となる。
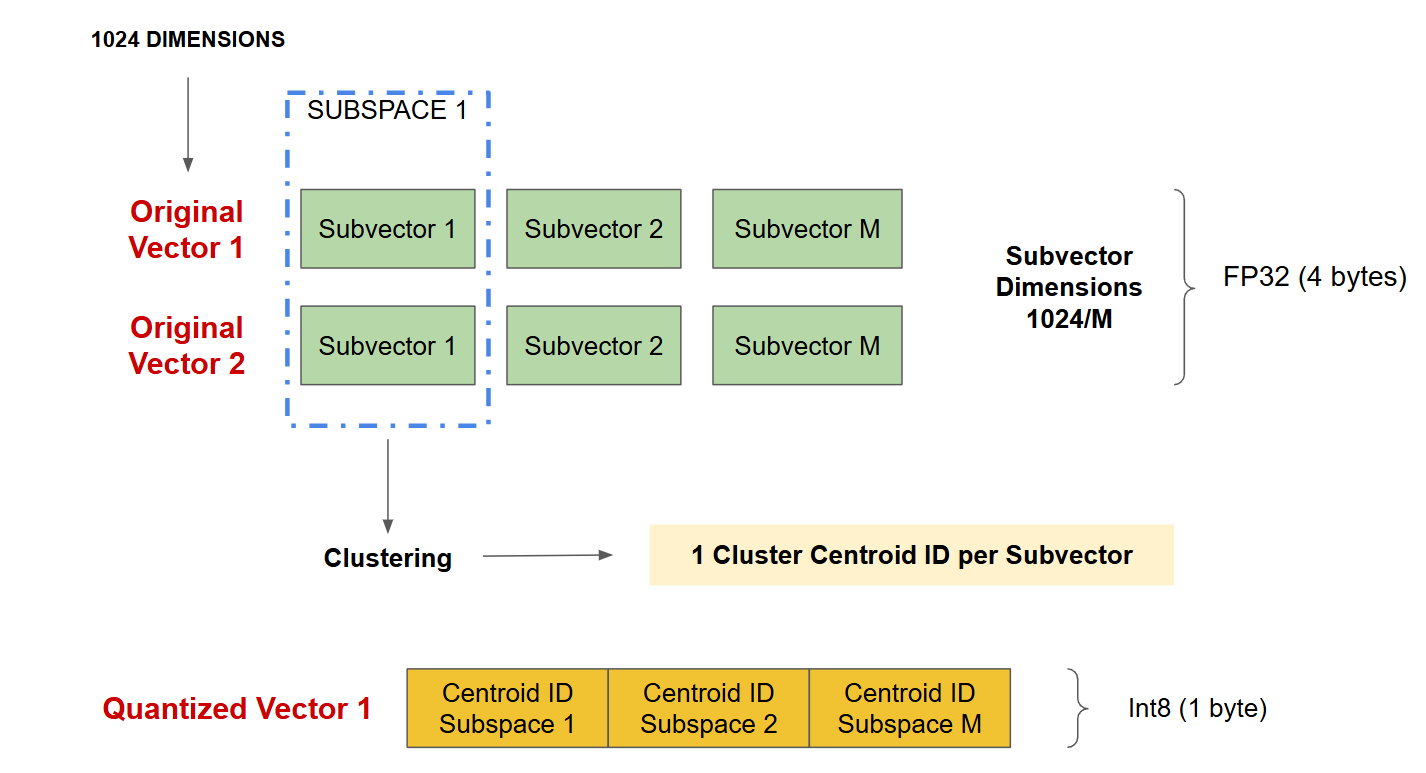図8 - 積の量子化.png
図8：積の量子化
この技法は、データの構造を保持したまま高圧縮を実現するため、効率的な保存と高速検索が不可欠なアプリケーションに効果的です。ただし、PQはスカラー量子化よりも精度に与える影響が大きく、圧縮率が高いほど損失も大きくなる。Milvusは現在、IVF_PQとSCANN(Scalable Nearest Neighbors)というPQを実行する2つのインデックスをサポートしている。最新のSCANNは、PQと異方性ベクトル量子化のような他の技術の組み合わせを適用し、データ分布に基づいた圧縮と、より高速な検索のためのSIMD(Single Instruction Multiple Data)演算を適応させている。
バイナリ量子化
バイナリ量子化は、ベクトルの次元をシングルビットのみを使用するバイナリ表現に変換することでデータを圧縮するもう1つの手法である。この方法では、元のベクトルの各次元に 2 進値が割り当てられます。正の値は 1 で表され、負の値は 0 で表されます。この 2 進エンコーディングでは、各次元が元の浮動小数点値または整数値ではなく 1 ビット（0 または 1）で表されるため、ストレージ要件が大幅に削減されます。
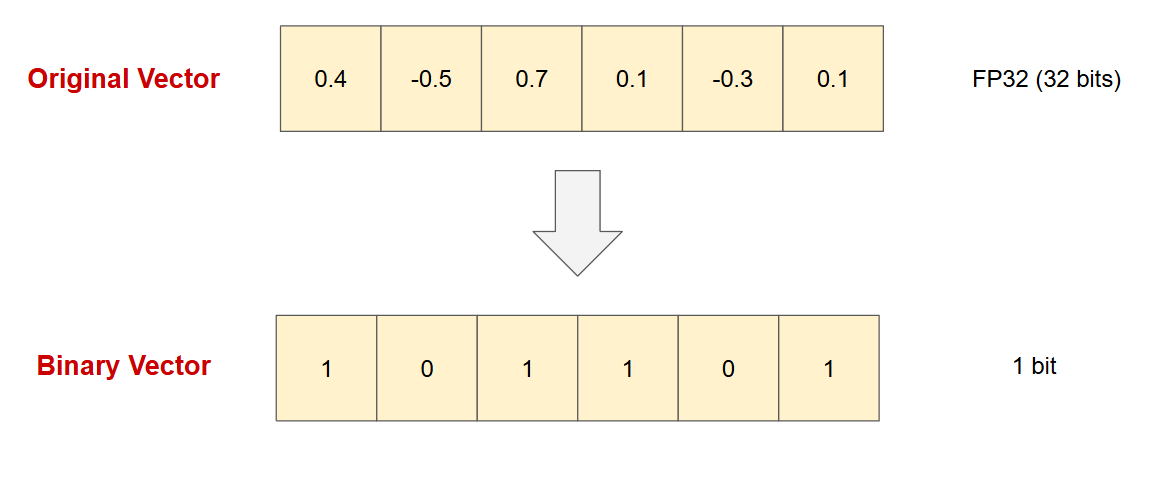図9 - バイナリ量子化.png
図9：バイナリ量子化
バイナリ量子化は、メモリフットプリントを最大32倍まで大幅に削減し、探索速度を向上させますが、主に高次元のアプリケーションや、バイナリベクトルで事前にテストされた特定のモデルに適しています。すべてのモデルや次元サイズが精度の点で良い結果を出すわけではなく、性能はモデルごとに個別にテストされなければならない。さらに、バイナリ量子化とrescoreテクニックを組み合わせることで、最終的な精度を高めることができます。
図10 - ジャカード距離.png](https://assets.zilliz.com/Figure_10_Jaccard_Distance_678cc2a5d8.png)
図10：ハミング距離(Source)
Milvusでは、2つのインデックスタイプによりバイナリ量子化がサポートされています：
bin_flat：bin_flat：比較的小さな（百万規模の）データセットに依存するバイナリインデックス作成法。
bin_ivf_flat**：高速クエリ用に最適化されたinvertedファイルインデックス。
これらのインデックスはバイナリベクトル用に最適化されているが、余弦類似度、内積、ユークリッド距離のようなメトリクスをサポートする高次元ベクトルとは異なり、2つの異なる距離メトリクスをサポートする：
ハミング：Hamming：2つのバイナリベクトル間の異なるビット位置の数を測定し、正確なビットレベルの類似性を評価するのに便利。
Jaccard**：2つの2進ベクトルの交差と結合を考慮し、一致するビットの割合を評価する。
図10 - ハミング距離.png
図10: ジャカード距離 (Source)_。
ベクトル量子化におけるその他のテクニック
前のセクションでは、スカラー量子化、積量子化、バイナリ量子化という基本的な技法を取り上げました。これらは、Zilliz CloudやMilvusのようなベクトルデータベースで一般的に適用されています。しかし、ベクトル量子化(VQ)の分野は、ベクトルデータベースだけでなく、様々なアプリケーションで広く使用されている高度なアルゴリズムの幅広いセットを包含しています。
このセクションでは、Lloydのアルゴリズム、Linde-Buzo-Grayアルゴリズム、Residual Quantization、Tree-Structured Vector Quantizationなど、いくつかの追加VQテクニックを紹介します。
ロイドのアルゴリズム（ナイーブK平均クラスタリング）
Lloydのアルゴリズムは、一般的にナイーブK-Meansクラスタリングと呼ばれ、VQの基本的な技術であり、データポイントを、それぞれがセントロイドによって表される、異なるクラスタに整理します。このアルゴリズムは、データ点とその割り当てられたセントロイドとの間の距離の合計を縮めようとするものである。
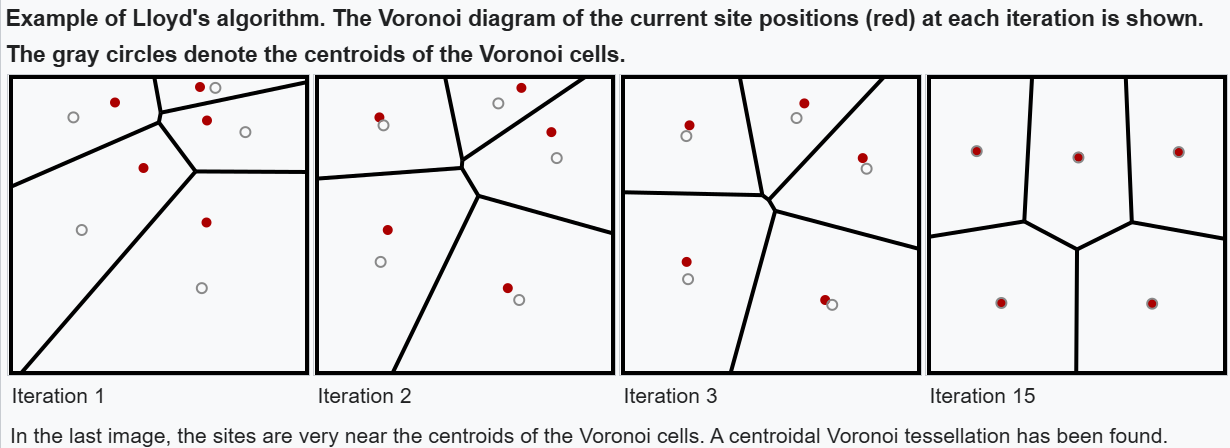図11 - ロイドのアルゴリズム.png
図11：ロイドのアルゴリズム (Source)_。
図11は、ロイドのアルゴリズムで形成されたクラスターを視覚的に表したボロノイ図です。各領域は特定の重心に最も近い領域に対応し、各点が他のどの点よりも割り当てられた重心に近いように、アルゴリズムが空間をどのように分割するかを効果的に示している。
アルゴリズムは反復プロセスで動作する：
1.初期化：指定されたクラスタ数（k）の初期セントロイドをランダムに選択することから始める。
2.割り当てステップ：各データポイントについて、ユークリッド距離のような選択された距離メトリックによって決定される、最も近いセントロイドにそれを割り当てる。
3.更新ステップ更新ステップ：現在クラスタに割り当てられているデータ点を平均することにより、各セントロイドを再計算します。
4.繰り返し： ステップ2と3を収束するまで繰り返す：
セントロイドの位置の変化が事前に定義された閾値以下になったとき。
最大反復回数に達した
データ点が安定したクラスタ割り当てを維持する
リンデ・ブゾ・グレイ（LBG）アルゴリズム
Linde-Buzo-Gray (LBG) Algorithm は、Lloyd's Algorithm をベクトル量子化専用に拡張したものです。LBGは、音声や画像データなど、データ圧縮に高い精度が要求される場面で特に有効であり、音声処理や画像処理で広く利用されている。
LBGアルゴリズムはLloydのものと同様の反復プロセスに従うが、重要な違いがある：初期セントロイドを生成するためにバイナリ分割アプローチを使用し、より構造的でバランスのとれたクラスタリング結果を保証する。手順は以下の通りです：
1.単一のセントロイドから始める：データセット全体の平均を最初のセントロイドとして計算する。
2.セントロイドを分割する：小さな値（摂動）を足したり引いたりすることで、各既存のセントロイドを2つに分割し、各反復でクラスタ数を2倍にする。
3.**ロイドのアルゴリズムを適用する：収束するまでロイドのアルゴリズムを使ってクラスターを絞り込む。
4.繰り返し：望ましいクラスタ数（コードブック・サイズ）になるまで分割と精密化を続ける。
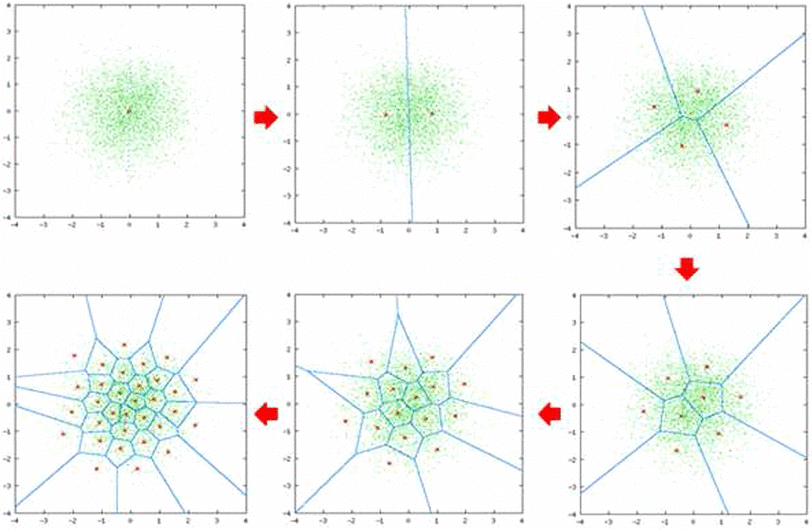図12 - リンデ・ブゾ・グレイ.png
図12：リンデ・ブゾ・グレイ（Source）_。
バイナリ分割を使用することで、LBGアルゴリズムは、ランダムな初期化方法よりもロバストなクラスタリングと、コンパクトなコードブックによるより良いデータ表現を実現します。
残差量子化(RQ)
Residual Quantization (RQ)は、複数の量子化段階を使用して、各ベクトルの近似を徐々に洗練させる階層的なVQ手法です。特に高次元データに有効で、RQは各ベクトルを表現する単一の重心に頼らず、各ベクトルを以前の近似からの残差（誤差）のシーケンスとして表現します。
その仕組みは次の通りです：
1.**最初の量子化各ベクトルはまず、初期コードブックから最も近いセントロイドで近似されます。
2.残差の計算：元のベクトルと近似ベクトルとの差（残差）が計算されます。
3.さらなる量子化：残差を二次コードブックで量子化し、より細かいディテールを捉える。
4.繰り返し：このプロセスはいくつかの量子化ステージで繰り返され、各ステージで前の近似からの残差を捕捉する。
最終的なベクトル表現は、すべての量子化ステージの合計となり、ステージが増えるごとに、より正確な近似が可能になります。
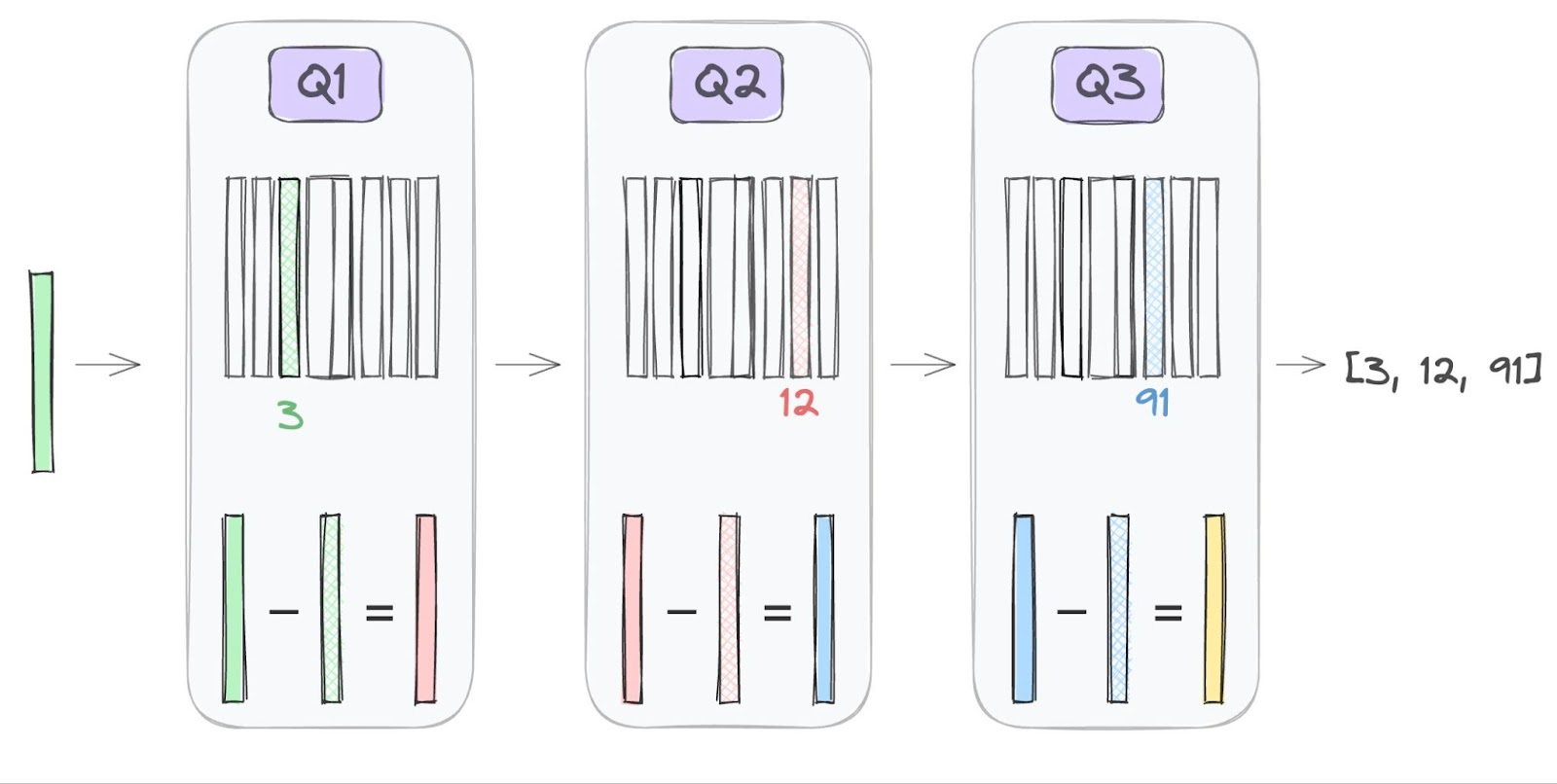図13 - 残差量子化.png
図13: 残差量子化(Source)
ツリー構造ベクトル量子化(TSVQ)
ツリー構造ベクトル量子化（TSVQ）は、ベクトルを階層的なツリー構造で整理し、各ノードが量子化の粒度の異なるレベルを表します。TSVQは、ルートノードから各ベクトルを最も正確に表すリーフノードへとツリーを走査することにより、効率的で階層的な検索とデータ圧縮を可能にします。
このプロセスには以下が含まれる：
1.バイナリ分割：LBGと同様に、TSVQはベクトル集合を2つのクラスタに分割することから始まる。
2.再帰的分割：各クラスタは再帰的に分割され、ノードが徐々に洗練された量子化レベルを表すツリー構造を生成する。
3.ツリーの走査：TSVQはベクトルを符号化する際、木の枝を根から葉までたどることで最適なクラスタを見つける。各葉ノードは一意のクラスタ重心として機能する。
課題と考察
圧縮と精度のトレードオフ
VQにおける主な課題の1つは、データサイズの削減と情報の質の維持の間の適切なバランスを見つけることである。圧縮率を高めればメモリ使用量を劇的に削減できるが、その代償として精度が低下することが多い。たとえば、ビット幅をFP32からINT8に下げたり、積量子化を適用したりすると、量子化エラーが発生し、高次元データのより微細な情報が失われる可能性があります。画像認識や大規模言語モデルのようなアプリケーションでは、このような細部の損失が検索品質を低下させ、精度の低い結果をもたらす可能性がある。
圧縮の程度と許容できる精度のバランスを見つけることは非常に重要です。ニーズによっては、このトレードオフを最適化するために、ベクトル量子化パラメータを慎重に調整する必要があります。ユースケースによっては、たとえ精度が落ちるとしても、より高い圧縮率が優先されることもあります。また、元のデータの忠実度を維持することが、メモリ節約の最大化よりも優先される場合もある。このように、各ユースケースで許容できる情報損失を判断するには、慎重な評価が必要である。
計算オーバーヘッド
ベクトル量子化のプロセス、特に最初のクラスタリングとセントロイド計算のステップは、特に高次 元データを扱う場合、計算量が多くなります。しかし、一旦コードブックが確立されると、検索と探索のプロセスはより効率的になります。高次元のベクトルをより少ないセントロイドの集合で表現することで、検索空間は大幅に縮小され、クエリ処理時間の短縮につながる。これはVQの重要な利点であり、大規模な高次元データセットであっても、より効率的なデータの検索と取得を可能にする。
したがって、最初の量子化段階では計算オーバーヘッドが前面に出てくるが、結果として得られる圧縮表現は、システムの重要なオンライン利用時に大幅な性能向上につながる。ベクトル量子化ベースのソリューションの全体的な計算効率を確保するためには、VQと探索プロセスの入念な最適化が極めて重要である。
アプリケーション固有のチューニング
VQ の有効性と適切なテクニックは、特定のデータタイプ、次元数、および意図するアプリ ケーションによって大きく異なります。例えば、テキスト埋め込みの圧縮に最適な量子化パラメータは、画像特徴ベクトルの圧縮に最適な量子化パラメータとは異なる場合があります。
VQの導入を成功させるには、多くの場合、対象とするユースケースに適した圧縮、精度、計算効率のバランスを見つけるために、慎重な実験とチューニングが必要です。VQ戦略がアプリケーションのニーズを満たし続けるためには、反復的な改良と継続的な監視が極めて重要である。
結論
まとめ：ベクトル量子化の主な手法
1.スカラー量子化 浮動小数点数（FP32など）をINT8のような単純なフォーマットに変換します。これにより、値がより小さな範囲にマッピングされ、ストレージが節約されますが、精度がわずかに損なわれるため、データが縮小されます。
2.積量子化(PQ) 高次元ベクトルを小さな塊に分割し、セントロイドを使ってそれぞれを個別に圧縮します。これは大規模なデータセットには最適ですが、精度が若干低下する可能性があります。
3.バイナリ量子化 データをバイナリ値（0と1）に変換する。非常に効率的だが、特定のモデルやアプリケーションに最適。
4.残差量子化 各圧縮段階の後に残ったものに注目することで、データを段階的に洗練させる。高次元のベクトルを最小限の損失で処理するのに理想的です。
5.ツリー構造ベクトル量子化（TSVQ）* ベクトルをツリー状に整理し、効率的に検索します。各レベルはより洗練されたクラスタを表し、検索を高速化します。
考慮すべき課題
圧縮と精度**：圧縮しすぎると、特に画像認識のようなタスクでは精度が低下します。適切なバランスをとることが重要です。
処理コスト最初のクラスタリングは計算が重くなりますが、後の検索が速くなることで報われます。
すべてをまとめる：現代のAIにおけるVQの役割
ベクトル量子化は、特に高次元のベクトルデータにおいて、データ圧縮の強力なツールである。類似のデータポイントをグループ化し、代表的なセントロイドで表現することで、VQは本質的なデータパターンを保持しながら、ストレージと計算コストを大幅に削減することができます。これまで説明してきたように、スカラー、積、バイナリといった様々な量子化手法は、速度、メモリ効率、精度といったアプリケーションの要件に応じて、明確な利点とトレードオフを提供します。Linde-Buzo-GrayアルゴリズムやTree-Structured Vector Quantizationのような他の手法は、大規模で複雑なデータセットの処理におけるVQの汎用性をさらに示しています。
これらの量子化手法は、現代のアプリケーション、特に大規模言語モデル（LLM）やZilliz CloudやMilvusのようなベクトルデータベースのような様々なAI技術によって駆動されるアプリケーションにおいて、データ集約的なタスクを拡張するために不可欠である。圧縮と精度の間には常にバランスが必要だが、VQ手法の継続的な開発により、精度をあまり妥協することなくストレージと処理能力を最適化できる。データ量が増加し続ける中、VQはビッグデータ時代において、より高速で効率的な保存と検索を可能にする重要な技術革新分野であり続けるだろう。
Benito MartinFreelance Technical Writer
