Learn
Exploring Vector Database Use Cases

Proximity Graph-based Approximate Nearest Neighbor Search

Dec 20, 202111 min read

Learn what PG-based ANNS is and how to optimize the algorithm to achieve a trade-off between search accuracy and efficiency.

By Mengzhao Wang

Read the entire series

What is ANNS?

ANNS stands for approximate nearest neighbor search, and it is an underlying backbone that supports various applications including image similarity search systems, QA chatbots, recommender systems, text search engines, and information retrieval systems. ANNS uses a well-designed index to instantly find the k nearest neighbors to a given query despite the growing size of a dataset. The index in ANNS helps save the trouble of calculating the distance between the query and each vector in the dataset, ultimately achieving a trade-off between accuracy and search latency by slightly sacrificing search accuracy for substantial improvement in search efficiency. [1]

According to the index adopted, the existing ANNS algorithms can be divided into four major types:

Hashing-based
Tree-based
Quantization-based
Proximity graph (PG)-based

Recently, PG-based ANNS algorithms have emerged as it is highly effective. Thanks to these PG-based algorithms, more accurate results can be achieved without having to compare and evaluate more vectors in the dataset.

How does PG-based ANNS work?

PG-based ANNS builds a nearest neighbor graph G = (V,E) as an index on the dataset S. V stands for the vertex set and E for edge set. Any vertex v in V represents a vector in S, and any edge e in E describes the neighborhood relationship among connected vertices. The process of looking for the nearest neighbor of a given query is implemented through a “proper routing strategy”, which determines the routing path from the entry to the result vertex. As such, we can illustrate the PG-based ANNS according to build PG and routing on PG.

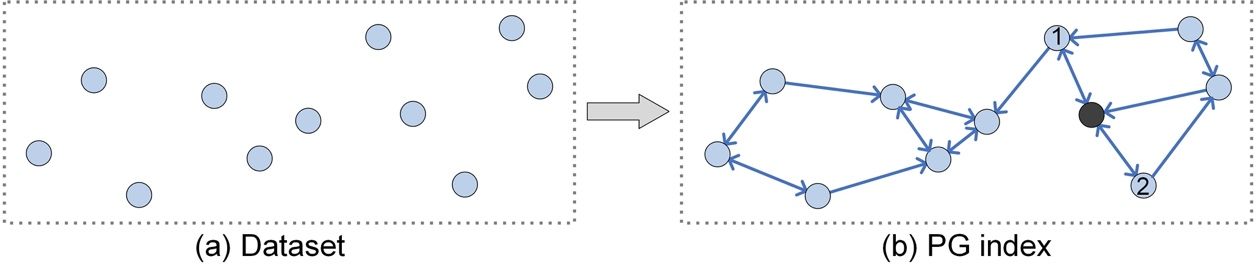Figure 1: Building a PG index (KNNG, k=2) on a toy dataset.

Build PG

Given a distance function d(,), one simple way to build a PG is to link every vertex to its k nearest neighbors in the dataset S. This process generates and builds an exact k nearest neighbor graph (KNNG). In KNNG, the vertices correspond to the points of the dataset S, and neighboring vertices (marked as x, y) are associated with an edge by evaluating their distance d(x, y). In Figure 1(b), the two vertices (numbered 1, 2) connected to the black vertex are its neighbors (k=2), and the black vertex can visit its neighbors along these edges (the arrows point from black vertex to its neighbors). To prevent the building process from being too complex, we can also consider approximate KNNG, as it can be constructed more quickly than exact KNNG.

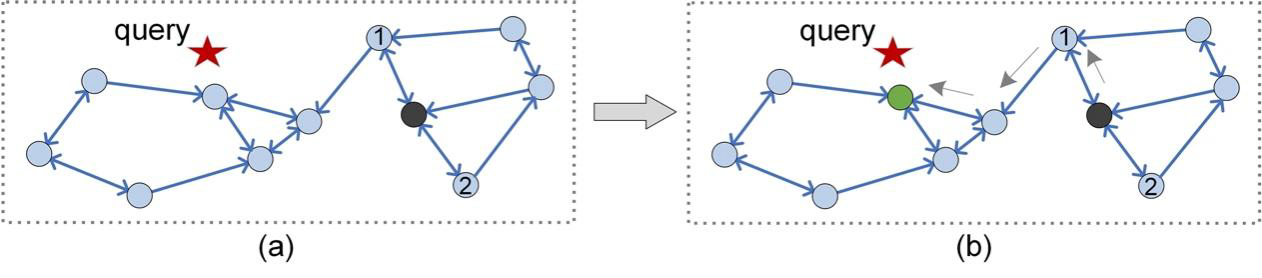Figure 2: Routing procedure on a PG index (KNNG, k=2).

Routing on PG

As shown in Figure 2, given a PG and a query q (the red star), PG-based ANNS aims to get a set of vertices that are close to q via routing. We take the case of returning q's nearest neighbor as an example to show how routing works. Initially, a seed vertex (the black vertex that can be randomly sampled or obtained by an additional index such as tree [16]) is selected as the result vertex r, and we can conduct routing from this seed vertex. Specifically, if d(n, q) < d(r, q), where n is one of the neighbors of r, r will be replaced by n. We repeat this process until the termination condition is met (e.g., for any n, d(n, q) ≥ d(r, q)), and the final r (the green vertex) is q's nearest neighbor.

How to improve PG-based ANNS?

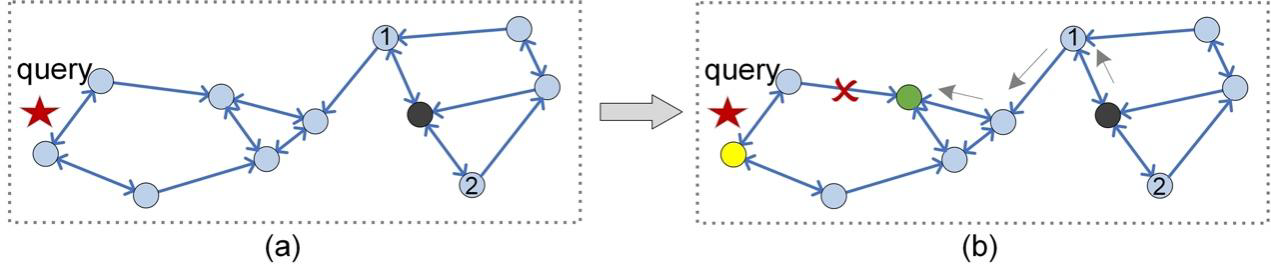Figure 3: Routing starting from the black vertex cannot reach the yellow vertex.

In Figure 2(b), you may have noticed that we cannot access all the other vertices by routing from the black vertex. Therefore, we argue that PG index (KNNG, k=2) has a worse connectivity than KGraph [2]. This will affect the search accuracy, measured by recall, when query q is located in an area that cannot be reached by routing. For example, for query q shown in Figure 3, we still perform routing from the black vertex, and then the routing will terminate at the green vertex. However, q's nearest neighbor is the yellow vertex rather than the green ones. Unfortunately, there is no route between the green vertex and the yellow vertex (the edge is directed), and thus we obtain an inaccurate result.

Therefore, we can improve the performance of PG-based ANNS algorithms from the following two perspectives.

PG index optimization

To solve the issue mentioned above, one simple method is to change all directed edges in KNNG to undirected edges (i.e., double arrow) (NSW [3], DPG [4]). As Figure 4(a) depicts, there is a path between any linked vertices. Therefore, for the same query as in Figure 3, when visiting the green vertex, we can continue to route along its neighbor (numbered 9 in Figure 4(b)), and finally terminate at the yellow vertex. However, adding a reverse edge to each directed edge will bring some extra vertex's neighbors (e.g., the vertex 1, 6 in Figure 4(a)), causing two problems: large index size and low search efficiency. It is easy to understand that the index size will be really large because we have to store more neighborhood relationships (22 neighbors in Figure 3, 28 neighbors in Figure 4). For low search efficiency, we can explain it using the example of routing from vertex 3 to vertex 7 (Figure 3(b) vs. Figure 4(b)). In KNNG (k=2, Figure 3(b)), distances, represented by the number of vertices to evaluate from query q, are calculated six times (i.e., the vertex numbered as 1, 2, 3, 6, 7, 8 in Figure 4). While in Figure 4(b), distances are calculated eight times (i.e., the vertex numbered as 1–8). Thus, extra calculation hampers search efficiency.

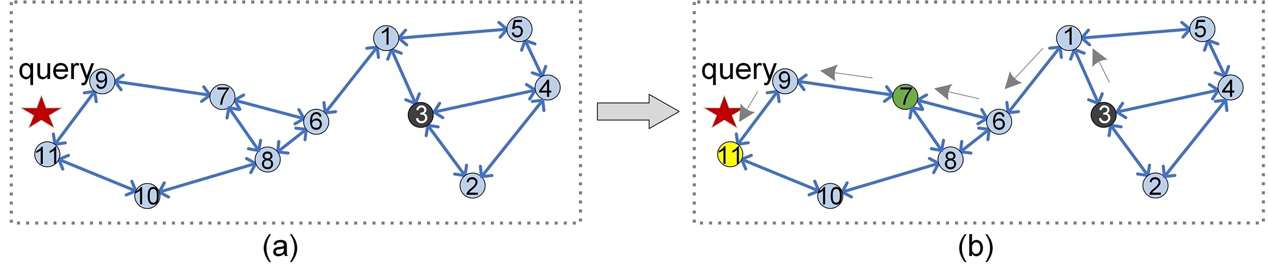Figure 4: Routing procedure on a modified KNNG index (add the reverse edge).

Another similar approach to optimization is to increase k, e.g., k=3 in Figure 5. Although we can reach the real nearest neighbor (the yellow vertex) of query q, this approach will result in the same problems as joining the reverse link (Figure 4).

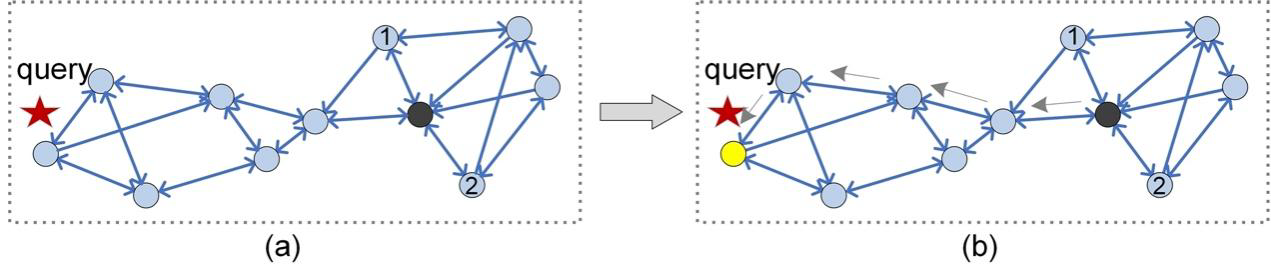Figure 5: Routing procedure on a KNNG index (k=3).

Now, we know that the above optimizations bring new problems for obtaining accurate search results. Is there a PG index that can tackle efficiency, accuracy, and index size simultaneously? After analyzing some state-of-the-art PG-based ANNS algorithms, we found that a kind of PG called relative neighborhood graph (RNG) is widely used.

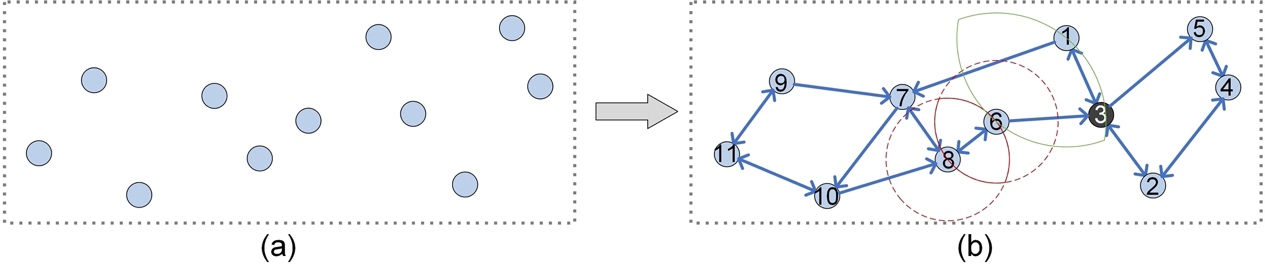Figure 6: Building a Relative Neighborhood Graph (RNG) on a toy dataset.

Before introducing the RNG construction process, we first define the concept of lune(,). As shown in Figure 6(b), we focus on the vertex 8 and 6, lune(8, 6) (the red lune) is formed by the intersection of two circles, which take the corresponding two vertices (i.e., the vertices numbered as 8, 6) as the center and the distance (i.e., d(8, 6)) as the radius [5].

Given a dataset S, for any two vertices (marked x, y), we use the following rules to determine whether the two are connected in RNG. Note that, for any vertex x, we assume that the following rules between x and other vertices (e.g., y) are judged in ascending order of distance value.

Rule1: For any vertex z (≠x, y) in S, if z is not in lune(x, y), then we link x and y with a bidirectional edge.
Rule2: For any vertex z (≠x, y) in lune(x, y), if there is no directed edge from x (or y) to z, then we link x (or y) to y (or x) with a directional edge.

The RNG in Figure 6(b) is built according to Rule1 and Rule2 (for any two vertices in S). For example, there are no other vertices in lune(8, 6) (the red lune), so vertices 8 and 6 are connected by a bidirectional edge (aka, undirected edge); while for vertices 6 and 1, there exists a vertex 3 in lune(6, 1) (the green lune), which is linked a directed edge with both vertices 6 and 1 (i.e., 6→3 and 1→3), thus we do not link 6 (or 1) to 1 (or 6).

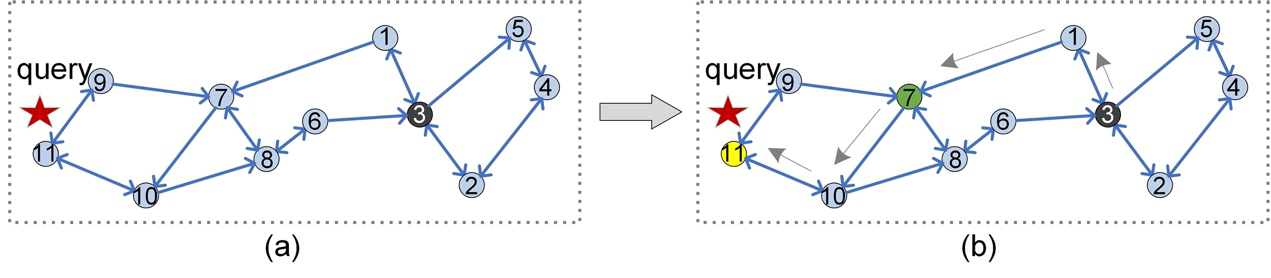Figure 7: Routing procedure on a Relative Neighborhood Graph (RNG).

As shown in Figure 7(b), for the same query q as Figure 3(b), the routing on RNG obtains accurate search result (the yellow vertex). In addition, compared with Figure 4(b) and 5(b), Figure 7(b) shows a smaller index size and higher search efficiency. For example, Figure 7(b) only needs to storage 22 neighbors (22 neighbors in Figure 3, 28 neighbors in Figure 4, 33 neighbors in Figure 5); and for the routing from vertex 3 to vertex 7, the number of distance calculations is five (six in Figure 3(b), eight in Figure 4(b), seven in Figure 5(b)).

Hence, almost all state-of-the-art PG-based ANNS algorithms (e.g., HNSW [6], NSG [5]) add an approximation of RNG. Nevertheless, RNG is not perfect (such as high index construction complexity), we still need to improve it to further meet the needs of practice.

Search optimization

You can notice that the above optimized PGs share the same routing strategy for search. Actually, several current PG-based ANNS algorithms, such as HNSW [6], NSG [5], adopt straightforward and greedy search as their routing strategy throughout the whole routing process. Although greedy search is easy to implement, it faces the limitation of low routing efficiency. This limitation is illustrated in Figure 7(b). When routing is performed on PG with greedy search, neighbors of each vertex to visit are fully explored. In other words, the distance from all neighbors of each vertex on routing path (indicated by arrows) to the query is computed, which inevitably becomes time-consuming. For example, we do not need to evaluate d(2, q) and d(5, q) when accessing vertex 3.

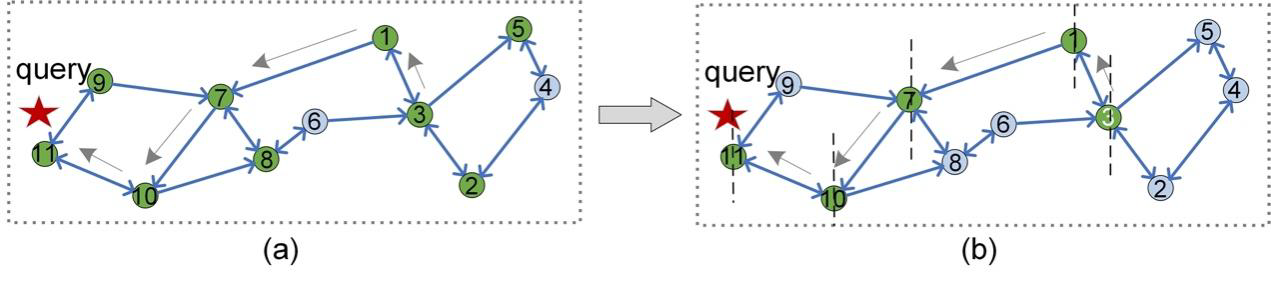Figure 8: The number of distance calculations (the number of green vertices) for different routing strategy for a given query on the same PG.

To solve this problem, an optimized routing strategy called guided search is proposed in "Hierarchical clustering-based graphs for large scale approximate nearest neighbor search" [8]. In a guided search, only neighbors in the same direction as the query are visited. Therefore, routing is greatly accelerated. Figure 8 compares how many times the distances are calculated in two different routing stategies: greedy search and guided search. Given a query q (the red star) and the seed vertex (numbered 3), greedy search visits nine vertices (all green vertices in Figure 8(a)) during routing, while guided search only visits five vertices (all green vertices in Figure 8(b)). Guided search only focuses on a visiting vertex's neighbors on the side of the vertical dotted line where q is located.

However, guided search still has some limitations, as pointed out in "Two-stage routing with optimized guided search and greedy algorithm on proximity graph" [7]. Recently, some machine learning-based approaches to optimization are proposed to improve the routing [9, 10], and these approaches generally obtain better trade-off between efficiency and accuracy at the price of more time and memory consumption [1].

Performance

Refer to "Benchmarking nearest neighbors"[11] for a comparison between PG-based ANNS algorithms and other methods (e.g., PQ). For the performance of different PG-based ANNS algorithms, refer to "A Comprehensive Survey and Experimental Comparison of Graph-Based Approximate Nearest Neighbor Search" [1] for more details.

Future Prospects

It is worth noting that almost all state-of-the-art algorithms are based on RNG (e.g., HNSW and NSG). The RNG-based optimization is still a promising research direction for PG-based ANNS. On the basis of the core algorithm, researchers are refining and improving PG-based ANNS algorithms' performance via hardware [14]. Other literatures add quantitative or disk-based schemes to cope with data increases [15]. To meet hybrid query (it only searches vectors that satisfy the label constraints) requirements, the latest research adds structured label constraints to the search process of PG-based ANNS algorithms [12, 13].

References

[^2] Dong W, Moses C, Li K. Efficient k-nearest neighbor graph construction for generic similarity measures[C]. Proceedings of the 20th international conference on World Wide Web (WWW). 2011: 577–586.

[^3] Malkov Y , Ponomarenko A , Logvinov A , et al. Approximate nearest neighbor algorithm based on navigable small world graphs[J]. Information Systems (IS), 2014, 45(SEP.): 61–68.

[^4] Li W, Zhang Y, Sun Y, et al. Approximate nearest neighbor search on high dimensional data—experiments, analyses, and improvement[J]. IEEE Transactions on Knowledge and Data Engineering (TKDE), 2019, 32(8): 1475–1488.

[^5] Fu C, Xiang C, Wang C, et al. Fast approximate nearest neighbor search with the navigating spreading-out graph[J]. Proceedings of the VLDB Endowment, 2019, 12(5): 461–474.

[^6] Malkov YA, Yashunin DA. Efficient and robust approximate nearest neighbor search using hierarchical navigable small world graphs[J]. IEEE transactions on pattern analysis and machine intelligence (TPAMI). 2018, 42(4): 824–836.

[^7] Xu X, Wang M, Wang Y, et al. Two-stage routing with optimized guided search and greedy algorithm on proximity graph[J]. Knowledge-Based Systems. 2021, 229: 107305.

[^8] Munoz JV, Goncalves MA, Dias Z, et al. Hierarchical clustering-based graphs for large scale approximate nearest neighbor search[J]. Pattern Recognition (PR). 2019, 96: 106970.

[^9] Li C, Zhang M, Andersen DG, et al. Improving approximate nearest neighbor search through learned adaptive early termination[C]. Proceedings of the International Conference on Management of Data (SIGMOD). 2020: 2539–2554.

[^10] Baranchuk D, Persiyanov D, Sinitsin A, et al. Learning to route in similarity graphs[C]. International Conference on Machine Learning (ICML). 2019: 475–484.

[^11] Benchmarking nearest neighbors[EB/OL]. [2021-12-12]. https://github.com/erikbern/ann-benchmarks.

[^12]Wang J, Yi X, Guo R, et al. Milvus: A Purpose-Built Vector Data Management System[C]. Proceedings of the International Conference on Management of Data (SIGMOD). 2021: 2614–2627.

[^13] An open source vector similarity search engine[EB/OL]. [2021-06-12] https://milvus.io/scenarios.

[^14] Zhao W, Tan S, Li P. SONG: Approximate nearest neighbor search on GPU. IEEE 36th International Conference on Data Engineering (ICDE). 2020: 1033–1044.

[^15] Subramanya SJ, Devvrit F, Simhadri HV, et al. DiskANN: Fast accurate billion-point nearest neighbor search on a single node[C]. Advances in Neural Information Processing Systems (NeurIPS). 2019, 13771–13781.

[^16] Iwasaki M. Pruned bi-directed k-nearest neighbor graph for proximity search[C]. International Conference on Similarity Search and Applications. 2016: 20-33.

About the author

Mengzhao Wang achieved his master's degree in computer science at Hangzhou Dianzi University. His research mainly focuses on proximity graph-based vector similarity search, and multi-modal search. And three patents in related field are filed under his name. Mengzhao has published two papers at VLDB Conference, and Knowledge-based Systems (KBS), an international and interdisciplinary peer-reviewed academic journal in the field of artificial intelligence.

During his spare time, Mengzhao loves playing the guitar and table tennis. He also loves running and reading. You can follow him on GitHub.