学習
ベクターデータベース入門：知っておくべきことすべて

おおよその最近接者ああ（迷惑）

May 25, 20234 分で読めます

効率と精度を向上させる近似最近傍探索に革命をもたらす革新的なアルゴリズム、Annoyの能力をご覧ください。

シリーズ全体を読む

#はじめに

ベクターデータベース101](https://zilliz.com/blog?tag=39&page=1)へようこそ。

前回のチュートリアルでは、HNSW (Hierarchical Navigable Small Worlds) について深く掘り下げてみました。HNSWはグラフベースのインデックス作成アルゴリズムで、今日ではベクトルデータベースで使用される最も一般的なインデックス作成戦略の1つです。

このチュートリアルでは、趣向を変えてツリーベースのベクトルインデックスについて説明します。具体的には、Approximate Nearest Neighbors Oh Yeah (Annoy)、木の森を使って最近傍探索を行うアルゴリズムについて説明します。ランダムフォレストや勾配ブースト決定木に慣れている人にとっては、Annoyはこれらのアルゴリズムの自然な拡張のように見えるかもしれません。HNSWのチュートリアルと同様に、まずAnnoyがどのように動作するのかを高レベルで説明し、その後にシンプルなPython実装を開発します。

アンノイの基本

HNSWが連結グラフとスキップリストに基づいて構築されているのに対して、Annoyはバイナリ探索木をコアデータ構造として使用している。Annoy(および他のツリーベースのインデックス)のキーとなる考え方は、ベクトル空間を繰り返し分割し、分割された部分集合のみを最近傍探索するというものです。これがIVFのように聞こえるなら、その通りだ。考え方は同じだが、実行方法が少し違う。

迷惑、可視化

Annoyを理解する最良の方法は、1本の木がどのように構築されるかを視覚化することである。ただし、高次元超空間は直感的な観点から2D/3Dユークリッド空間とは大きく異なるので、以下の画像は参考程度に覚えておいてほしい。

まずはインデクシングから。Annoyの場合、これは再帰的な処理で、呼び出しスタックの最大サイズがツリーの深さになる。最初の反復では、2つのランダムなデータセット・ベクトル a と b が選択され、a と b の両方から等距離にある超平面に沿って全超空間が分割される。そして、超空間の「左」半分のベクトルはツリーの左半分に割り当てられ、部分空間の「右」半分のベクトルはツリーの右半分に割り当てられる。これは超平面そのものを実際に計算しなくてもできることに注意してください - すべてのデータセット・ベクトルについて、a（左）とb（右）のどちらが近いかを決定する必要があります。

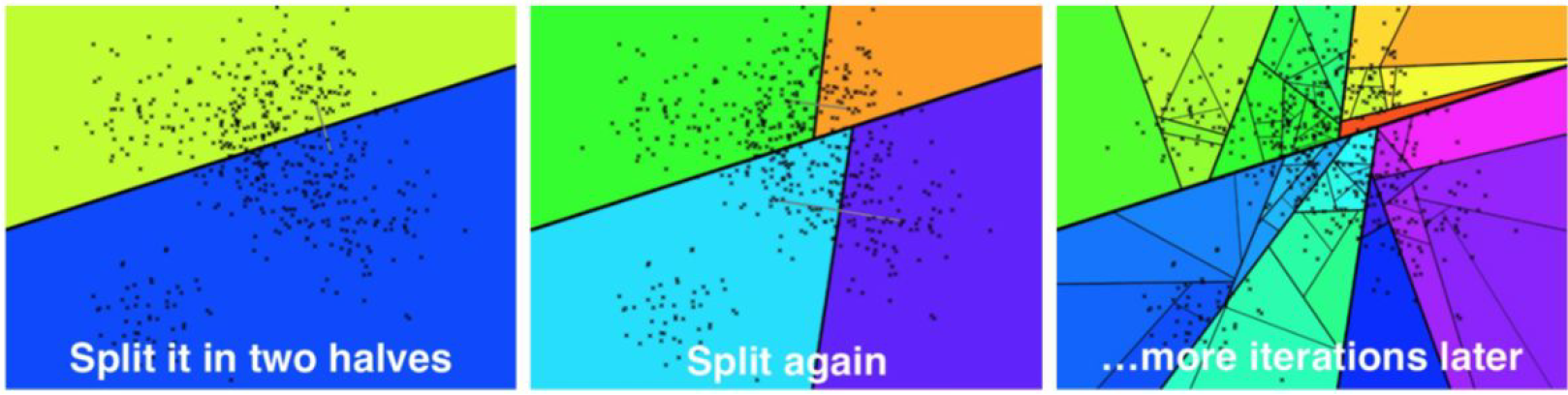
それぞれ1回目、2回目、N回目の反復の後。ソース。

2回目の反復は、1回目の反復で生成された左と右の部分木の両方に対してこのプロセスを繰り返し、深さ2と4つの葉ノードを持つ木になる。この処理は3回目、4回目、そしてそれ以降の反復でも、葉ノードがあらかじめ定義された要素数Kより少なくなるまで続けられる。オリジナルのAnnoy実装では、Kはユーザーが設定できる変数値である。

インデックスが完全に構築されたので、次はクエリに移ります。あるクエリーベクトルqが与えられると、ツリーを走査して検索することができる。超平面は各中間ノードを分割し、左右のベクトルとの距離を計算することで、クエリベクトルが超平面のどちらに位置するかを決定することができます。このプロセスを、最大でも K 個のベクトルの配列を含むリーフノードに到達するまで繰り返す。そして、これらのベクトルをランク付けしてユーザに返すことができる。

Annoyの実装

Annoyがどのように機能するかがわかったところで、実装を始めよう。いつものように、まず（128次元の）ベクトルのデータセットを作る：

python

np として numpy をインポートする。 dataset = np.random.normal(size=(1000, 128))


まず、左右のサブツリーを含む `Node` クラスを定義する：

python
クラス Node(object)：
    """ベクトルの集合で初期化し、`split()`を呼び出す。
    """

    def __init__(self, ref: np.ndarray, vecs: List[np.ndarray])：
        self._ref = ref
        self._vecs = vecs
        self._left = None
        self._right = なし

    プロパティ
    def ref(self) -> Optional[np.ndarray]：
        """n-dハイパースペースにおける参照点。ルートノードであれば `False` と評価される。
        """
        return self._ref

    プロパティ
    def vecs(self) -> List[np.ndarray]：
        """このリーフノードのベクトル。リーフでない場合は `False` と評価される。
        """
        return self._vecs

    プロパティ
    def left(self) -> Optional[object]：
        """左ノード。
        """
        return self._left

    プロパティ
    def right(self) -> Optional[object]：
        """右ノード。
        """
        return self._right

vecs変数には、ノード内のすべてのベクトルのリストが格納される。このリストの長さがある値Kよりも小さい場合、これらのベクトルはそのまま残ります。そうでない場合、これらのベクトルはleftとrightに伝搬され、vecs[0]とvecs[1]` が超平面を分割するために使用されるランダムに選択された2つのベクトルとして残ります。

それでは、インデックスの作成に移ろう。まず、ツリーの各ノードは、ランダムに選択された2つのデータセットベクトルを結ぶ線に直交する超平面によって分割されることを思い出してください。便利なことに、距離を計算することで、クエリベクトルが超平面のどちらに位置するかを決定することができる。いつものように、この計算にはNumPyのベクトル化数学を使います：

python def _is_query_in_left_half(q, node)：

クエリベクトルが左半分にあれば `True` を返す

dist_l = np.linalg.norm(q - node.vecs[0]) dist_r = np.linalg.norm(q - node.vecs[1]) return dist_l < dist_r


それでは、実際のツリーの構築に移ろう。

``python
インポートランダム


def split_node(node, K: int, imb: float) -> bool：

    # 停止条件: リーフノードの最大ベクトル数
    if len(node._vecs) <= K：
        return False

    # 最大5回の反復を続ける
    for n in range(5)：
        left_vecs = [].
        right_vecs = [].

        # 2つのランダムインデックスを取り、左半分と右半分に設定する。
        left_ref = node._vecs.pop(np.random.randint(len(node._vecs)))
        right_ref = node._vecs.pop(np.random.randint(len(node._vecs)))

        # ベクトルを半分に分割
        for vec in node._vecs：
            dist_l = np.linalg.norm(vec - left_ref)
            dist_r = np.linalg.norm(vec - right_ref)
            if dist_l < dist_r：
                left_vecs.append(vec)
            else：
                right_vecs.append(vec)

        # ツリーがほぼバランスしていることを確認する
        r = len(left_vecs) / len(node._vecs)
        if r < imb and r > (1 - imb)：
            node._left = Node(left_ref, left_vecs)
            node._right = Node(right_ref, right_vecs)
            真を返す

        # アンバランスが大きい場合、ツリー構築処理をやり直す
        node._vecs.append(left_ref)
        node._vecs.append(right_ref)

    偽を返す


def _build_tree(node, K: int, imb: float)：
    """ツリーを構築するために左半分と右半分を再帰する。
    """
    node.split(K=K, imb=imb)
    if node.left：
        _build_tree(node.left, K=K, imb=imb)
    if node.right：
        _build_tree(node.right, K=K, imb=imb)


def build_forest(vecs: List[np.ndarray], N: int = 32, K: int = 64, imb: float = 0.95) -> List[Node]：
    """`N`本の森を構築する。
    """
    forest = []"
    for _ in range(N)：
        root = Node(None, vecs)
        _build_tree(root, K, imb)
        forest.append(root)
    return forest

これはより密度の高いコードブロックなので、順を追って見ていこう。まず、初期化済みの Node が与えられたら、ランダムに2つのベクトルを選択し、データセットを左右に分割する。次に、先ほど定義した関数を使用して、サブベクトルが2つの半分のどちらに属するかを決定する。ツリーのバランスを保つために imb パラメータを追加したことに注意してください。ツリーの片側が全サブベクトルの 95% 以上を含む場合、分割処理をやり直します。

ノードの分割が完了すると、build_tree 関数はすべてのノードに対して再帰的に呼び出される。リーフノードは K 以下のサブベクトルを含むものとして定義される。

検索範囲を大幅に縮小できるバイナリツリーを構築できた。では、クエリーも実装してみましょう。問い合わせはとても簡単で、興味のある枝に到達するまで、左または右の枝に沿って連続的に移動しながらツリーを走査します：

python def _query_linear(vecs: List[np.ndarray], q: np.ndarray, k: int) -> List[np.ndarray]： return sorted(vecs, key=lambda v: np.linalg.norm(q-v))[:k].

def query_tree(root: Node, q: np.ndarray, k: int) -> List[np.ndarray]： """単一の木に問い合わせる。 """

while root.left and root.right：
    dist_l = np.linalg.norm(q - node.left.ref)
    dist_r = np.linalg.norm(q - node.right.ref)
    root = root.left if dist_l < dist_r else root.right

# 最も近い近傍をブルートフォースサーチ
return _query_linear(root.vecs, q, k)


このコードの塊は貪欲にツリーを走査し、1つの最近傍（`nq = 1`）を返します。しかし、私たちは複数の最近傍を見つけることにしばしば興味があることを思い出してください。さらに、複数の最近傍は他のリーフノードにも存在する可能性があります。では、どうすればこれらの問題を解決できるのでしょうか？

## 走れ、森よ、走れ

(そう、[アメリカの古典](https://en.wikipedia.org/wiki/Forrest_Gump)では、主人公の名前の綴りが "Forrest "であることに気づいている)。

以前のIVFのチュートリアル](https://zilliz.com/learn/vector-index)では、クエリベクトルに最も近いボロノイセルを超えて検索を拡大することがよくあったことを思い出してください。クエリ・ベクトルがセル・エッジに近い場合、最も近い近傍ベクトルが隣のセルにある可能性が非常に高いからです。このような「エッジ」は高次元空間ではより一般的であるため、高い再現性が必要な場合は `nprobe` の大きな値がよく使われる。

ツリーベースのインデックスでも同じ問題に直面します。最も近い近傍のノードが最も近いリーフノード/ポリゴンの外にある場合があります。Annoyは、1)分割の両側の検索を許可し、2)ツリーの_forest_を作成することでこれを解決する。

まず、前のセクションの実装を拡張して、分割の両側を検索してみましょう：

python
def _select_nearby(node: Node, q: np.ndarray, thresh: int = 0)：
    """_is_query_in_left_halfと同じように機能しますが、両方を返すことができます。
    """
    もしnode.leftでないか、node.rightでない場合：
        return ()
    dist_l = np.linalg.norm(q - node.left.ref)
    dist_r = np.linalg.norm(q - node.right.ref)
    if np.abs(dist_l - dist_r) < thresh：
        return (node.left, node.right)
    if dist_l < dist_r：
        return (node.left,)
    return (node.right,)


def _query_tree(root: Node, q: np.ndarray, k: int) -> List[np.ndarray]：
    """これは上記の `query_tree` 関数を置き換えるものである。
    """

    pq = [ルート］
    nns = []"
    while pq：
        ノード = pq.pop(0)
        nearby = _select_nearby(node, q, thresh=0.05)

        # もし `_select_nearby` がどちらのノードも返さなければ、リーフにいることになる。
        if nearby：
            pq.extend(nearby)
        else：
            nns.extend(node.vecs)

    # 最も近い近傍をブルートフォースサーチ
    return _query_linear(nns, q, k)


def query_forest(forest: List[Node], q, k: int = 10)：
    nns = set()
    for root in forest：
        # nns` をクエリ結果とマージする。
        res = _query_tree(root, q, k)
        nns.update(res)
    return _query_linear(nns, q, k)

次に、完全なインデックスを樹木の森として構築するための関数を追加する：

``python def build_forest(vecs: List[np.ndarray], N: int = 32, K: int = 64, imb: float = 0.95) -> List[Node]： """N本の森を構築する。 """ forest = []" for _ in range(N)： root = Node(None, vecs) _build_tree(root, K, imb) forest.append(root) return forest


すべてが実装されたので、IVF、SQ、PQ、HNSWで行ったように、今度はすべてをまとめてみよう：

python
from typing import List, Optional
インポートランダム

np として numpy をインポート


クラス Node(object)：
    """ベクトルの集合で初期化し、`split()`を呼び出す。
    """

    def __init__(self, ref: np.ndarray, vecs: List[np.ndarray])：
        self._ref = ref
        self._vecs = vecs
        self._left = None
        self._right = なし

    プロパティ
    def ref(self) -> Optional[np.ndarray]：
        """n-dハイパースペースにおける参照点。ルートノードであれば `False` と評価される。
        """
        return self._ref

    プロパティ
    def vecs(self) -> List[np.ndarray]：
        """このリーフノードのベクトル。リーフでない場合は `False` と評価される。
        """
        return self._vecs

    プロパティ
    def left(self) -> Optional[object]：
        """左ノード。
        """
        return self._left

    プロパティ
    def right(self) -> Optional[object]：
        """右ノード。
        """
        return self._right

    def split(self, K: int, imb: float) -> bool：

        # 停止条件: リーフノードの最大ベクトル数
        if len(self._vecs) <= K：
            return False

        # 最大5回の反復を続ける
        for n in range(5)：
            left_vecs = [].
            right_vecs = [].

            # 2つのランダムなインデックスを取り、左半分と右半分に設定する。
            left_ref = self._vecs.pop(np.random.randint(len(self._vecs)))
            right_ref = self._vecs.pop(np.random.randint(len(self._vecs)))

            # ベクトルを半分に分割
            for vec in self._vecs：
                dist_l = np.linalg.norm(vec - left_ref)
                dist_r = np.linalg.norm(vec - right_ref)
                if dist_l < dist_r：
                    left_vecs.append(vec)
                else：
                    right_vecs.append(vec)

            # ツリーがほぼバランスしていることを確認する
            r = len(left_vecs) / len(self._vecs)
            if r < imb and r > (1 - imb)：
                self._left = Node(left_ref, left_vecs)
                self._right = Node(right_ref, right_vecs)
                真を返す

            # アンバランスが大きい場合、ツリー構築プロセスをやり直す
            self._vecs.append(left_ref)
            self._vecs.append(right_ref)

        偽を返す


def _select_nearby(node: Node, q: np.ndarray, thresh: int = 0)：
    """_is_query_in_left_halfと同じように機能するが、両方を返すことができる。
    """
    もしnode.leftでないか、node.rightでない場合：
        return ()
    dist_l = np.linalg.norm(q - node.left.ref)
    dist_r = np.linalg.norm(q - node.right.ref)
    if np.abs(dist_l - dist_r) < thresh：
        return (node.left, node.right)
    if dist_l < dist_r：
        return (node.left,)
    return (node.right,)


def _build_tree(node, K: int, imb: float)：
    """ツリーを構築するために左半分と右半分を再帰する。
    """
    node.split(K=K, imb=imb)
    if node.left：
        _build_tree(node.left, K=K, imb=imb)
    if node.right：
        _build_tree(node.right, K=K, imb=imb)


def build_forest(vecs: List[np.ndarray], N: int = 32, K: int = 64, imb: float = 0.95) -> List[Node]：
    """`N`本の森を構築する。
    """
    forest = []"
    for _ in range(N)：
        root = Node(None, vecs)
        _build_tree(root, K, imb)
        forest.append(root)
    return forest


def _query_linear(vecs: List[np.ndarray], q: np.ndarray, k: int) -> List[np.ndarray]：
    return sorted(vecs, key=lambda v: np.linalg.norm(q-v))[:k].


def _query_tree(root: Node, q: np.ndarray, k: int) -> List[np.ndarray]：
    """単一の木に問い合わせる。
    """

    pq = [ルート］
    nns = [].
    while pq：
        ノード = pq.pop(0)
        nearby = _select_nearby(node, q, thresh=0.05)

        # もし `_select_nearby` がどちらのノードも返さなければ、リーフにいることになる。
        if nearby：
            pq.extend(nearby)
        else：
            nns.extend(node.vecs)

    # 最も近い近傍をブルートフォースサーチ
    return _query_linear(nns, q, k)


def query_forest(forest: List[Node], q, k: int = 10)：
    nns = set()
    for root in forest：
        # nns` をクエリ結果とマージする。
        res = _query_tree(root, q, k)
        nns.update(res)
    return _query_linear(nns, q, k)

これでAnnoyは終了だ！

まとめ

このチュートリアルでは、遊び心のある名前のツリーベースのインデックス戦略であるAnnoyを深く掘り下げました。インタプリタのオーバーヘッドのため、ベクトル探索データ構造を実装するにはPythonよりも良い言語があります。それでも、私たちはnumpyベースの配列計算を同じくらい使います。メモリを前後にコピーしないようにする最適化はたくさんできるが、読者のための練習として残しておこう。

次のチュートリアルでは、ソリッドステートハードドライブからの直接クエリに特化したユニークなグラフベースのインデックス作成アルゴリズムであるVamanaアルゴリズム（一般的にはDiskANNとしても知られています）の概要を説明しながら、インデックス作成戦略へのディープダイブを続けます。

このチュートリアルのコードはすべて私のGithubで自由に利用できます。

ベクターデータベース101コースをもう一度見てみよう

1.非構造化データ入門 2.ベクターデータベースとは 3.ベクトルデータベース、ベクトル検索ライブラリ、ベクトル検索プラグインの比較 4.Milvusの紹介 5.Milvusクイックスタート 6.ベクトル類似検索入門 7.ベクトルインデックスの基本と反転ファイルインデックス 8.スカラー量子化と積量子化 9.階層的航行可能小世界(HNSW) 10.近似最近傍オーイェー(ANNOY) 11.プロジェクトに適したベクトルインデックスの選択 12.DiskANNとVamanaアルゴリズム

article.updateAt

Frank Liu
Frank Liu is the Director of Operations & ML Architect at Zilliz, where he serves as a maintainer for the Towhee open-source project. Prior to Zilliz, Frank co-founded Orion Innovations, an ML-powered indoor positioning startup based in Shanghai and worked as an ML engineer at Yahoo in San Francisco. In his free time, Frank enjoys playing chess, swimming, and powerlifting. Frank holds MS and BS degrees in Electrical Engineering from Stanford University.