学習
ベクターデータベース入門：知っておくべきことすべて

ソフトマックス活性化関数の解読

Apr 03, 20241 分で読めます

この記事では、ソフトマックス活性化関数、その応用、課題、より良いパフォーマンスのためのヒントについて説明する。

シリーズ全体を読む

ソフトマックス活性化関数のデコード

この記事では、ソフトマックス活性化関数について、その応用、課題、より良いパフォーマンスを得るためのヒントについて説明します。その数学的基礎を探り、他の活性化関数と比較し、実践的な実装例を提供します。

活性化関数入門

活性化関数はニューラルネットワーク(NN)に非線形性を導入し、生の入力を意味のある出力に変換します。非線形性がなければ、ニューラルネットワークは線形回帰モデルであり、あるニューロンの結果を別のニューロンに渡すだけである。活性化関数は、意思決定に重要なニューロンを決定し、次の層に渡すためにそれらを活性化することによって、ニューラルネットワークが複雑なパターンを学習することを可能にする。

ソフトマックス活性化関数とは？

ソフトマックス関数は正規化指数関数としても知られ、主にマルチクラス分類に使用される一般的な活性化関数です。前述のシグモイド活性化関数のように、他の活性化関数は2値分類に限定されていますが、ソフトマックス関数は複数クラスのラベルに対応します。

ソフトマックス関数はニューラルネットワークからの生の出力の入力ベクトルを受け取り、それらを確率の配列にスケーリングします。確率の配列では、各確率は各クラスラベルが存在する可能性を表し、配列の合計は1になる。最も高い確率を持つクラスが、ニューラルネットワークによる最終予測として選択される。

ソフトマックス活性化関数の式は次のとおりである：

f(xi) = e^xi / Σj e^xj

ここで

x = ニューラルネットワークの前の層からの生の出力のベクトル

i = クラスiの確率

e = 2.718

ロジットを確率にスケーリングして、それらの値を1まで加算することで、モデルの予測の解釈可能性が高まります。これらの確率は信頼スコアとして解釈でき、モデルが最も高い確率を持つクラスを選ぶ決定を強制する。

数学的直観

なぜソフトマックス関数が機能するのかを理解するために、それを分解してみよう：

1.指数化：各入力にe^xを適用することで、すべての値が正になるようにする。また、このステップは入力間の差を増幅する。

2.正規化：すべての指数化された値の合計で割ることで、出力が1になることを保証し、有効な確率分布を作成します。

3.相対スケール：関数の指数的性質は、入力を確率にマッピングする間、入力の相対的スケールを保持する。

ソフトマックス方程式の視覚化

数式を見ながら、ソフトマックス関数は以下のステップでロジットを確率に変換する：

ニューラルネットワークの最終層の出力層ベクトルを示す生のベクトルの各エントリーの指数を計算する。指数計算後、高いスコアはより顕著になり、低いスコアはさらに最小化され、どのスコアをアクティブにするかを示す。

ステップ1 指数を計算する ](https://assets.zilliz.com/raw_vector_9abd60609d.png)

ステップ1：各エントリーの確率分布の指数を全エントリーの指数の和で割る。これは指数化された値の確率和を確率に正規化する。

ステップ2: 各指数を指数和で割る。

ステップ2 各指数を指数和で割る ](https://assets.zilliz.com/step_2_a6c1cd7931.png)

正規化後の値は、各クラスの出力確率を表す。これらは最終的なソフトマックス出力を表すベクトルに整列される。

ステップ3 確率をベクトルに並べる

ステップ3 確率をベクトルに並べる ](https://assets.zilliz.com/step_3_6edd9c67b0.png)

ソフトマックス関数をPythonで実装する

Pythonでソフトマックス関数を実装するのは簡単だ。TensorFlowとPyTorchでそれぞれどのように実装できるか見てみよう：

TensorFlowでのソフトマックス関数

TensorFlowでは、Softmax活性化関数を実装するのは、Softmax関数で出力層を定義するのと同じくらい簡単だ：

from tensorflow.keras import layers

# ソフトマックス活性化で出力層を定義する
output_layer = layers.Dense(num_classes, activation="softmax")(hidden_layer_output)

# モデルをコンパイルする
model.compile(loss="categorical_crossentropy", optimizer="adam", metrics=["accuracy"])

上記のスニペットは以下を定義している：

num_classes：データセットに含まれるカテゴリの数。
hidden_layer_output：前のレイヤーの出力（ほとんどの場合、最後の隠れレイヤー）。
activation="softmax"：activation="softmax":活性化関数としてソフトマックスを使用するモデルを指定する。

あるいは、TensorFlowのnn.softmax関数を使えば、より直接的に制御できる：

tf として tensorflow をインポートする。

# ロジットにソフトマックスを適用
predictions = tf.nn.softmax(logits, axis=-1)

ここで

logits：最終隠れ層の出力。
axis=-1: 最後の次元にソフトマックス関数を適用する。

1.PyTorchのソフトマックス活性化関数

TensorFlowと同様に、PyTorchにもSoftmax関数が用意されており、シンプルな実装が可能です：

インポートトーチ

# ロジットにソフトマックスを適用
predictions = torch.nn.functional.softmax(logits, dim=1)

ここで

logits：最終隠れ層の出力。
axis=1: 最後の次元にソフトマックスを適用することを指定する。

PyTorchではnn.Softmax関数を使って専用のSoftmax層を作ることもできます：

import torch.nn as nn

# ソフトマックスレイヤーを作成する
softmax_layer = nn.Softmax(dim=1)

# レイヤーに出力を通す
predictions = softmax_layer(logits)

ここで

dim=1: 次元1に沿ってソフトマックスを適用することを指定する。

人工知能(AI)におけるソフトマックス活性化関数の応用

ソフトマックス活性化関数は、現実世界の多クラス機械学習問題を解決する。その中には以下のようなものがある：

1.画像の分類

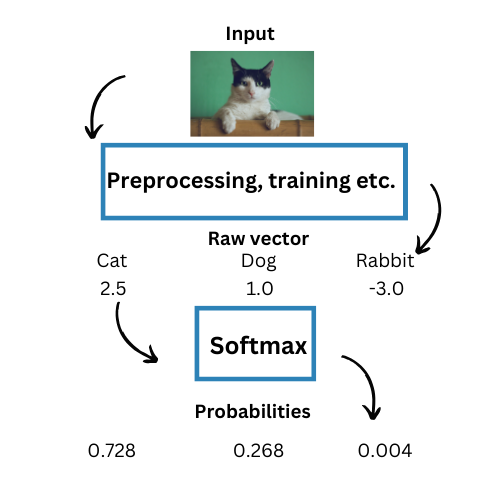
ニューラルネットワークは画像分類を得意とし、入力画像を分析し、あらかじめ定義されたクラスに分類する。ソフトマックス関数はこのプロセスで重要な役割を果たし、学習に基づいて各クラスに確率を割り当てる。最も高い確率を持つクラスが、モデルの最終出力として選ばれる。

例えば、最終層にソフトマックス関数を使った畳み込みニューラルネットワーク(CNN)を考えてみよう。タスクは画像を「猫」、「犬」、「ウサギ」に分類することである。各クラスを構成する各ベクトルに割り当てられた確率を[0.728, 0.268, 0.004]とする。この場合、最も確率の高いソフトマックス出力ベクトルは "Cat "に割り当てられるので、これが最終出力となる。

1.感情分析

ツイッターのセンチメント分析は、ソフトマックス関数の応用としてよく知られている。さらに最近では、見出しが肯定的か、否定的か、中立的かを識別するAI見出し分析器も登場している。ソフトマックス活性化関数により、このようなことが可能になっている。

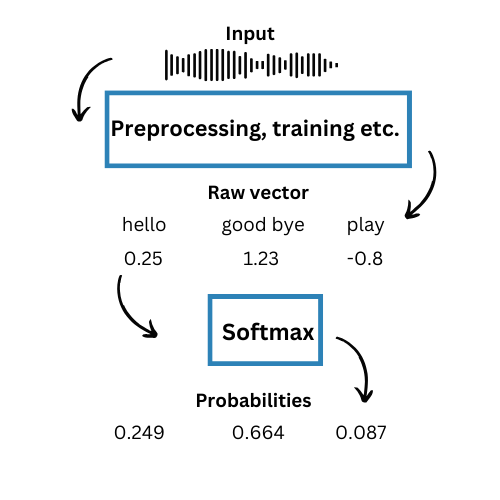
1.音声認識

AIチャットボットは、事前に定義された選択肢の入力配列からユーザーの単語を正確に識別し、それに応じて応答を策定する必要があります。そこで、モデルは入力音声を分析し、可能性のある各単語の最大値のスコアを生成します。ソフトマックス関数は値を計算し、各選択肢に確率を割り当てることができます。例えば

ソフトマックスの課題とベストプラクティス

活性化関数の課題を事前に考慮することで、正確で効率的な分類が可能になります。予防策を講じることで、モデルの精度が向上します。ソフトマックス関数はマルチクラスや分類タスクに頑健ですが、限界もあります。しかし、ベストプラクティスに従い、効率的なパフォーマンスを確保することで、これらの制限を緩和することができます。

1.不均衡なデータセット

あるクラスが他のクラスよりも多いデータセットは、ソフトマックスの活性化をミスリードします。その結果、多数派のクラスが高い確率を受け取ることになる。

ベスト・プラクティス多数派のクラスからいくつかのレコードを削除するか、少数派のクラスをオーバーサンプリングしていくつかのレコードを重複させると、バランスのとれたデータセットになる。誤分類に大きなペナルティを与えるコスト関数は、少数クラスを学習し、正確な確率を達成するために、モデルを[prompt](https://zilliz.com/glossary/prompt-as-code--engineering appendix))することができる。

1.数値的不安定性

ロジットが大きい場合、その指数関数がオーバーフローを起こし、極端に大きな数になることがある。反対に、ロジットが極端に小さい場合、その指数関数がゼロに近くなることがあります。これらは、オーバーフローエラー、不正確な出力値や確率分布、その他の数値的安定性や不安定性につながる可能性があります。

ベストプラクティス一貫性のある](https://zilliz.com/blog/understand-consistency-models-for-vector-databases)スケールでデータを最大値に正規化することは、数値の不安定性を防ぎます。Log-Softmax関数は、オーバーフローエラーの課題を軽減するために使用することもできます。これは2つのSoftmax値と出力の対数を計算し、より小さな数値に変換することで機能します。

クロスエントロピー損失との関係

Softmaxは、マルチクラス分類モデルを学習する際に、クロスエントロピー損失と併用されることが多い。クロスエントロピー損失関数は特にソフトマックスとの使用に適しています：

1.1.予測された確率分布と真の分布の間の非類似度を測定する。

2.ソフトマックスと併用することで、滑らかで凸の最適化ランドスケープを提供します。

ソフトマックスによるクロスエントロピー損失の式は以下の通り：

L = -Σ_i y_i * log(softmax(x_i))

ここで、y_i は真のラベル（通常、ワンホットエンコーディング）、softmax(x_i) はクラスi の予測確率である。

結論

ソフトマックス活性化関数は、そのシンプルさと解釈のしやすさから広く使われている。データセットの各クラスにソフトマックスの値や確率を割り当てることで、正確な意思決定を導き、最も確率の高いクラスを出力として適するようにする。

ソフトマックス関数がどのように機能するかを理解することは、AIや分類タスクにおいて極めて重要である。ソフトマックス関数は、生のニューラル出力を、合計が1になる正規化された確率に変換し、さまざまなアプリケーションで信頼性の高い意思決定を可能にする。どのツールの課題にも対処できるベストプラクティスは存在するが、トレードオフは常に存在する。その機能とベストプラクティスを理解することで、適切なトレードオフを行い、その可能性を最大限に活用することができる。

Softmax関数を実際のプロジェクトで使用し、そのアプリケーションを試して、理解を深めてください。

その他のリソースニューラルネットワーク活性化関数のリスト

よりよく理解するために](https://zilliz.com/blog/use-vector-search-to-better-understand-computer-vision-data) ソフトマックスを他の一般的な活性化関数と比較してみましょう：

バイナリステップ関数

バイナリステップ関数はニューラルネットワークで使われる活性化関数で、閾値に基づいてニューロンを活性化すべきかどうかを決定する。この関数への入力がしきい値を超えると、ニューロンは活性化されて値 1 を出力し、そうでない場合は非活性化されて値 0 を出力する。

リニア

活性化関数（「活性化なし」関数と呼ばれることもある）は、入力に指定値を乗じた実数値を返す。

リラク(RelU)

ReLU（Rectified Linear Unit）関数は、ニューラルネットワークでよく使われる活性化関数です。入力が正ならそのまま出力し、負ならゼロを出力します。正の入力に対しては線形関数のように振る舞うが、ReLUは負の値に対してゼロ出力を導入するため非線形である。

ReLUの重要な特徴の1つは、入力に応じて1か0のどちらかになる単純な導関数のため、効率的なバックプロパゲーションを可能にすることである。このためReLUは計算効率が高く、ディープ・ネットワークの学習に役立つ。

重要なのは、ReLUはすべてのニューロンを同時に活性化するのではなく、線形変換から正の出力を持つニューロンだけを活性化することである。負の入力を持つニューロンは非活性化され、事実上ゼロを出力し、いかなる信号も前進させない。

タン

入力ベクトルの双曲線正接を返す活性化関数。この関数を隠れ層に使用すると、勾配が消失するなどの学習上の問題が発生しやすくなります。

式：tanh(x) = (e^x - e^(-x))/ (e^x + e^(-x))
使用例隠れ層、しかしReLUより一般的ではない
限界：グラデーションの消失に悩まされる

シグモイド(ロジスティック)

入力のシグモイド関数を返す活性化関数。このシグモイド関数は、勾配の消失などの学習問題に対するモデルの影響を大きくするため、隠れ層では使用すべきではありません。

式：σ(x) = 1 / (1 + e^(-x))
使用例バイナリ分類
制限制限：単一クラスに対する出力範囲[0,1

エルユー

Exponential Linear Unit (ELU) はニューラルネットワークで使用される活性化関数で、ReLU 関数の変形です。負の入力に対してゼロを出力するReLUとは異なり、ELUは指数曲線を使用して関数の負の部分の傾きを修正します。具体的には、負の入力値に対して、ELUは平坦なゼロではなく、滑らかな曲線の値を出力し、ReLUで見られる「死んだニューロン」の問題を軽減するのに役立つ。

Leaky ReLUやParametric ReLUが、負の入力値に対して小さな一定の傾き（直線）を導入し、複数の出力を行うのとは対照的に、ELUは負の値に対して対数曲線を適用する。この曲線により、ELUは活性度の平均をゼロに近づけることができ、機械学習のスピードアップに貢献し、入力の変化に対してよりロバストなモデルにすることができます。