学習
ベクターデータベース入門：知っておくべきことすべて

階層的航行可能小世界（HNSW）

Jul 17, 20243 分で読めます

HNSW(Hierarchical Navigable Small World)は、ベクトルデータベースにおいて近似最近傍(ANN)検索を行うグラフベースのアルゴリズムである。

シリーズ全体を読む

***最新更新：7月26日

前回のチュートリアルでは、スカラー量子化と積量子化という、検索の範囲を狭めることなくデータベース全体のサイズを小さくする2つのベクトルインデックス戦略について見てきました。スカラー量子化と積量子化がどのように機能するかをよりよく説明するために、Pythonで独自のバージョンも実装しました。

このチュートリアルでは、今日最も一般的に使用されている一次アルゴリズムを見ることで、その知識をベースにしていきます：Hierarchical Navigable Small Worlds (HNSW)です。 Hierarchical Navigable Small World (HNSW)はグラフベースのアルゴリズムで、ベクトルデータベースにおいて近似最近傍探索(ANN)を行います。HNSWアルゴリズムは、速度と精度の点でANN検索を非常によく実行し、信じられないほどロバストなベクトル検索アルゴリズムになっています。 残念ながら、人気があるにもかかわらず、HNSWアルゴリズムを理解するのは難しいかもしれません。

HNSWの基本

以前のチュートリアルで、ベクトル検索インデックスには、ハッシュベース、ツリーベース、クラスターベース、グラフベースの4つのタイプがあることを思い出してください。HNSWは後者のグラフインデックスアルゴリズムにしっかりと当てはまります。HNSWは、確率スキップリストとNavigable Small World (NSW)グラフという2つの核となる概念を組み合わせている。まず、HNSWアルゴリズムについて説明する前に、この2つのコンセプトを個別に掘り下げてみよう。

確率スキップ・リストとは何か？

まずは確率スキップリスト。よく知られたデータ構造で、各要素が次の要素へのポインタを保持する。リンクリストはスタックやキューのようなLIFOやFIFOのデータ構造を実装するのに適しているが、大きな欠点はランダムアクセスに関する時間の複雑さである：O(n)である。スキップリストは追加のレイヤーを導入することでこの問題を解決しようとするもので、余分なメモリ（通常のリンクリストがO(n)であるのに対し、O(n log n)の空間複雑度）と挿入と削除のための実行時オーバーヘッドを発生させることで、O(log n)`のランダムアクセス時間複雑度を可能にする。

確率スキップリストは多階層のリンクリストであり、上層は長い連結を維持する。 下層に行くにつれて、連結はどんどん短くなり、最下層はすべての要素を含む「元の」リンクリストとなる。下の図は、この確率スキップリストの構造を示している：

スキップリスト構造](https://assets.zilliz.com/skip_list_c08b630b31.png)

_{図解によるスキップリスト構造。高い層ほど要素が少ない。}

スキップリストの要素iに到達するために、最も高い層から始める。i`より大きいリストの要素に対応するノードを見つけたら、前のノードに戻り、下の層に移動します。これを、探している要素が見つかるまで続ける。2つのオブジェクトの大きさを直接比較する方法が必要なので、スキップリストはソートされたリストに対してのみ機能することに注意してください。

挿入は確率的に行われる。どんな新しい要素に対しても、まず、その要素が最初に現れるレイヤーを見つけ出す必要がある。一番上のレイヤーが最も確率が低く、レイヤーが下がるにつれて確率が高くなる。一般的なルールは、あるレイヤーにある要素は、あらかじめ定義された確率 p でその上のレイヤーに現れるというものである。したがって、ある要素が最初にあるレイヤー l に現れた場合、その要素は l-1、l-2...とレイヤーに追加されていくことになる。

バランススキップリストが標準的なリンクリストより性能が劣ることはあり得ますが、その確率は信じられないほど低いことに注意してください。

Navigable Small World (NSW)とは?

さて、スキップリストの話はここまでにして、ナビゲーブル・スモール・ワールド（NSW）について説明しよう。NSWはグラフベースのアルゴリズムで、データセット内の近似最近傍を見つけるものです。ここでの一般的な考え方は、まずネットワーク上の多数のノードを想像することである。各ノードは他のノードに対して短距離、中距離、長距離の接続を持つ。ベクトル探索を行う場合、あらかじめ定義されたエントリーポイントから始める。そこから他のノードへの接続を評価し、見つけたいノードに最も近いノードにジャンプする。このプロセスを、最も近い隣人を見つけるまで繰り返します。

このような探索はgreedy searchと呼ばれます。このアルゴリズムは数百、数千ノードの小さなNSWには有効ですが、はるかに大きなNSWでは破綻する傾向があります。各ノードの短距離、中距離、長距離接続の平均数を増やすことでこの問題を解決できますが、これはネットワーク全体の複雑さを増し、探索時間が長くなります。各ノードがデータセット内の他の全てのノードに接続されているような絶対的に「最悪」のケースでは、NSWはナイーブな（線形）探索よりも優れていない。

NSWはクールだが、これはベクトル探索とどう関係するのだろうか？ここでのアイデアは、データセットの全てのベクトルをNSWの点と想像することで、長距離の接続は互いに非類似のベクトルによって定義され、近距離の接続はその逆である。ベクトルの類似性スコアは、類似性メトリックで測定されることを思い出してください - 通常、浮動小数点ベクトルではL2距離（ユークリッド距離とも呼ばれる）または内積（IP）、バイナリベクトルではJaccardまたはハミング距離です。

データセットベクトルを頂点とする航行可能なスモールワールドグラフ(NSW graph)を構築することで、クエリベクトルに近い頂点に向かってNSWを貪欲に走査することで、効率的に最近傍探索を行うことができる。

HNSW (Hierarchical Navigable Small Worlds)とは？

ベクトル検索やベクトル類似検索の場合、数億から数十億のベクトルからなるデータセットを持つことが多い。このような規模では、平凡なNSWはあまり有効ではないので、より優れたグラフ構造が必要になる。

better_graph.png

_HNSW.

を入力してください。

HNSWはスキップリストの概念を借りてNSWを拡張したものである。スキップリストのように、HNSWはリンクリストの代わりにNSWだけで、複数の層（それゆえ、Hierarchical Navigable Small Worldという用語がある）を維持する。HNSWグラフの最上位層にはノードがほとんどなく、最長リンクがあり、最下位層にはすべてのノードと最短リンクがある。検索プロセスでは、最上層であらかじめ定義された点を入力し、貪欲にクエリーベクトルに最も近い近傍ノードに向かう。最も近いノードに到達したら、このプロセスをHNSWグラフの第2層まで繰り返す。これを最も近い近傍に到達するまで続ける。

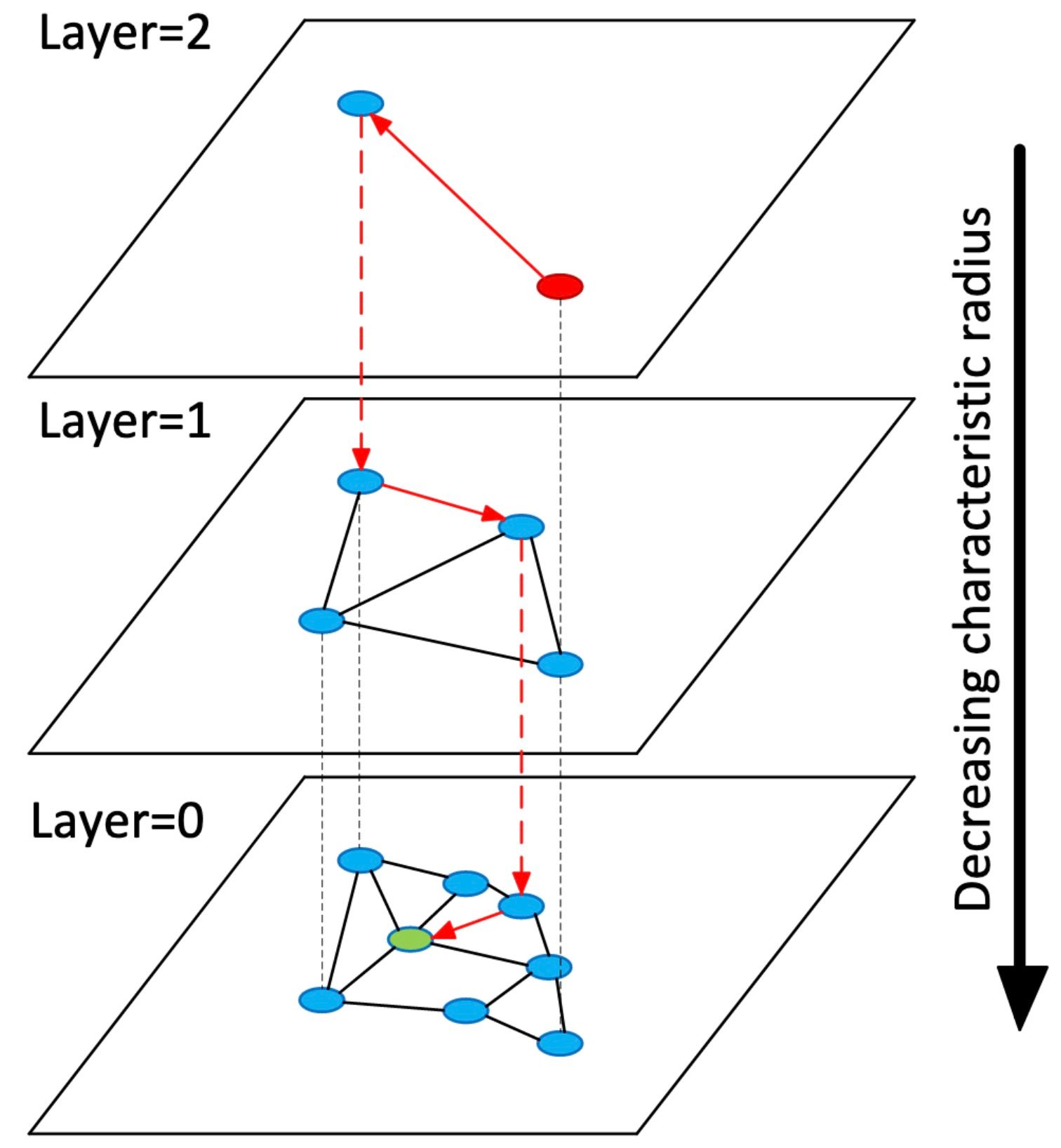hnsw_visualized_hnswグラフ.jpg

_{階層グラフの概念を視覚化したHNSW論文の図。https://arxiv.org/abs/1603.09320}

より。

挿入はスキップリストと同様に機能する。あるベクトルvに対して、我々はまずグラフの最初の層を走査し、その最も近い近傍を見つけてから、その下の層に移動する。次に、グラフを再度走査し、2番目のレイヤーで最も近い隣人を見つける。このプロセスは、一番下のグラフの最近傍に到達するまで続く。

ここから、どのリンク（頂点間の接続）を作成するかを決定しなければならない。ここでも、追加できる双方向リンクの最大数を決めるパラメータMをあらかじめ設定しておく。これらのリンクは通常vの最近傍に設定されるが、他のヒューリスティックを使用することもできる。ベクトルが現れると仮定して、同じプロセスを上位層で繰り返す。

スキップリストと同様に、クエリーベクトルは指数関数的に減少する確率で上位層に現れる。具体的には、HNSWの論文ではfloor(-ln(rand(0, 1)))という式を用いている。ここで、rand(0, 1)は(0, 1]の間の一様分布からサンプリングした乱数である。これは、特定の層における2つの頂点/ベクトル間の最小距離を制約していないことに注意してください。しかし、このようなことが起こる確率は、特にHNSWインデックスのベクトル数をスケールアップするにつれて、信じられないほど低くなる。

HNSWの実装方法

HNSWは些細なことではないので、ここでは基本的なバージョンだけを実装する。いつものように、（128次元の）ベクトルのデータセットを作ることから始めよう：

python

np として numpy をインポートする。 dataset = np.random.normal(size=(1000, 128))


最初のステップは、HNSWインデックスを構築することである。そのためには、各ベクトルをデータセットに追加する必要がある。そこで、まずインデックスを保持するデータ構造を作りましょう。この基本的な例では、各レイヤー/グラフに対応する内側のリストでインデックスを表現するためにリストのリストを使用します：

python
>>> L = 5 # 5層のHNSW
>>> index = [[] for _ in range(L)] # 5層のHNSW

各グラフの各要素は、ベクトル、そのベクトルがグラフ内でリンクするインデックスのリスト、その下のレイヤーの対応するノードのインデックスを含む3タプルである。一番下のレイヤでは、3-タプルの3番目の要素は None に設定される。

すべての挿入はまずグラフの最近傍を検索する必要があるので、まずそれを実装しよう。このように、インデックスのサブグラフを走査することができる：

python def _search_layer(graph, entry, query, ef=1)：

best = (np.linalg.norm(graph[entry][0] - query), entry)

nns = [best］
visit = set(best) # 訪問ノードの集合
candid = [best] # 最近傍に挿入するノードの候補
heapify(candid)

# 上位k個の最近接ノードを見つける
while candid：
    cv = heappop(candid)

    if nns[-1][0] < cv[0]：
        ブレーク

    # 候補ベクトルの最近傍をループする
    for e in graph[cv[1]][1]：
        d = np.linalg.norm(graph[e][0] - query)
        if (d, e) not in visit：
            visit.add((d, e))

            # より良い」ベクトルだけを候補ヒープに入れる
            if d < nns[-1][0] or len(nns) < ef：
                heappush(candid, (d, e))
                insort(nns, (d, e))
                if len(nns) > ef：
                    nns.pop()

return nns


このコード・スニペットはより複雑だが、説明があれば理解しやすいだろう。ここでは、ヒープを使って優先キューを実装し、それを使ってグラフ内の最近傍ベクトルを順番に並べます。これまでの例と同様に、ここではL2距離（ユークリッド距離）を使っていますが、このコードは他の[距離メトリック](https://zilliz.com/blog/similarity-metrics-for-vector-search)にも拡張できます。まずヒープにエントリーポイントを入れる。

ここで行っているのは、_greedy_探索の実装だけである。nns`は最近接点の出力リストであり、`candid`は候補点のヒープである。つまり、まず `candid` 内の "最良 "ベクトルに対する全ての最近傍ベクトルを評価し、より良い（より良いとはクエリベクトルに近いという意味である）ベクトルを出力リストである最近傍リストと候補点のヒープに追加し、次の繰り返しで評価する。これは2つの停止条件のどちらかに達するまで繰り返される：評価する候補点がなくなるか、今以上に良くできないと判断するかである。

top-kグラフ検索が終わったので、HNSWインデックス全体を検索するためのトップレベル`search`関数を実装することができる：

python
def search(index, query, ef=1)：

    # インデックスが空の場合は空のリストを返す
    if not index[0]：
        return [].

    best_v = 0 # 初期最適頂点をエントリポイントに設定する
    for graph in index：
        best_d, best_v = _search_layer(graph, best_v, query, ef=1)[0].
        if graph[best_v][2]：
            best_v = graph[best_v][2]: グラフを検索する。
        else：
            return _search_layer(graph, best_v, query, ef=ef)

まずエントリーポイント（一番上のグラフの0番目の要素）から始め、一番下のレイヤーに到達するまで、各インデックスレイヤーで最近傍を探索する。最下層にいる場合、3タプルの最後の要素は None に解決されることを思い出してください。最下層に到達したら、 best_v をエントリーポイントとしてグラフを検索する。

HNSWのインサートに戻ろう。まず、どのレイヤーに新しいベクトルを挿入するかを考えなければならない。これはかなり簡単だ：

python def _get_insert_layer(L, mL)： # ml は分布を正規化するための乗法係数です。 l = -int(np.log(np.random.random()) * mL) return min(l, L)


すべての準備が整ったので、挿入関数を実装することができます。

``python
def insert(self, vec, efc=10)：

    # インデックスが空の場合、ベクトルを全レイヤーに挿入して返す
    if not index[0]：
        i = なし
        for graph in index[::-1]：
            graph.append((vec, [], i))
            i = 0
        リターン

    l = _get_insert_layer(1/np.log(L))

    start_v = 0
    for n, graph in enumerate(index)：

        # レイヤー[l, L]に対してのみ挿入を行う
        if n < l：
            _, start_v = _search_layer(graph, start_v, vec, ef=1)[0].
        else：
            node = (vec, [], len(_index[n+1]) if n < L-1 else None)
            nns = _search_layer(graph, start_v, vec, ef=efc)
            for nn in nns：
                node[1].append(nn[1]) # NNへのアウトバウンド接続
                graph[nn[1]][1].append(len(graph)) # ノードへのインバウンド接続
            graph.append(node)

        # 開始頂点を次のレイヤの最近傍に設定する。
        start_v = graph[start_v][2］

インデックスが空の場合、すべてのレイヤに vec を挿入してすぐにリターンする。これはインデックスを初期化し、後でうまく挿入できるようにするためである。インデックスに既にデータが格納されている場合は、前のステップで実装した get_insert_layer 関数を使用して挿入レイヤーを計算します。そこから、一番上のグラフのベクトルの最近傍を見つける。このプロセスは、挿入レイヤーである l に到達するまで、その下のレイヤーに対して続けられる。

層 l とその下のすべての層について、まず vec に最も近い近傍ノードをあらかじめ決められた数 ef まで見つける。次に、ノードから最近傍への接続を作成し、その逆も同様である。適切な実装では、初期のベクトルが他のベクトルに接続されすぎないようにするための刈り込み技術も必要であることに注意してほしい。

これで、検索（クエリー）と挿入の両方の機能が完成しました。すべてをクラスにまとめてみましょう：

python from bisect import insort from heapq import heapify, heappop, heappush

npとしてnumpyをインポートする

from ._base import _BaseIndex

class HNSW(_BaseIndex)：

def __init__(self, L=5, mL=0.62, efc=10)：
    self._L = L
    self._mL = mL
    self._efc = efc
    self._index = [[] for _ in range(L) ]。

静的メソッド
def _search_layer(graph, entry, query, ef=1)：

    best = (np.linalg.norm(graph[entry][0] - query), entry).

    nns = [best］
    visit = set(best) # 訪問ノードの集合
    candid = [best] # 最近傍に挿入するノードの候補
    heapify(candid)

    # 上位k個の最近接ノードを見つける
    while candid：
        cv = heappop(candid)

        if nns[-1][0] > cv[0]：
            ブレーク

        # 候補ベクトルの最近傍をループする
        for e in graph[cv[1]][1]：
            d = np.linalg.norm(graph[e][0] - query)
            if (d, e) not in visit：
                visit.add((d, e))

                # より良い」ベクトルだけを候補ヒープに入れる
                if d < nns[-1][0] or len(nns) < ef：
                    heappush(candid, (d, e))
                    insort(nns, (d, e))
                    if len(nns) > ef：
                        nns.pop()

    return nns

def create(self, dataset)：
    for v in dataset：
        self.insert(v)

def search(self, query, ef=1)：

    # インデックスが空の場合は、空のリストを返す
    if not self._index[0]：
        return []

    best_v = 0 # 初期最適頂点をエントリポイントに設定する
    for graph in self._index：
        best_d, best_v = HNSW._search_layer(graph, best_v, query, ef=1)[0].
        if graph[best_v][2]：
            best_v = graph[best_v][2]: グラフ[best_v][2]。
        else：
            return HNSW._search_layer(graph, best_v, query, ef=ef)

def _get_insert_layer(self)：
    # ml は分布を正規化するための乗法係数である。
    l = -int(np.log(np.random.random()) * self._mL)
    return min(l, self._L-1)

def insert(self, vec, efc=10)：

    # インデックスが空の場合、ベクトルを全レイヤーに挿入して返す。
    if not self._index[0]：
        i = None
        for graph in self._index[::-1]：
            graph.append((vec, [], i))
            i = 0
        リターン

    l = self._get_insert_layer()

    start_v = 0
    for n, graph in enumerate(self._index)：

        # レイヤー[l, L]に対してのみ挿入を行う
        if n < l：
            _, start_v = self._search_layer(graph, start_v, vec, ef=1)[0].
        else：
            node = (vec, [], len(self._index[n+1]) if n < self._L-1 else None)
            nns = self._search_layer(graph, start_v, vec, ef=efc)
            for nn in nns：
                node[1].append(nn[1]) # NNへのアウトバウンド接続
                グラフ[nn[1]][1].append(len(graph)) # ノードへのインバウンド接続
            graph.append(node)

        # 開始頂点を次のレイヤの最近傍に設定する。
        start_v = graph[start_v][2］


完了！

## HNSW のまとめ

このチュートリアルではHNSW(Hierarchical Navigable Small Worlds)と呼ばれるグラフベースのベクトル類似検索について説明しました。このHNSWアルゴリズムは最大限のクエリパフォーマンスを求めるMilvusユーザーにとってしばしば選択されるものです。

次回のチュートリアルでは、近似最近傍Oh Yeah（ANNOY）-その遊び心のある名前から私が特に気に入っているツリーベースのインデックス作成アルゴリズム-でインデックス作成戦略へのディープダイブを続けます。



## ベクターデータベース101コースをもう一度見てみましょう。

1.[非構造化データ入門](https://zilliz.com/learn/introduction-to-unstructured-data)
2.[ベクターデータベースとは](https://zilliz.com/learn/what-is-vector-database)
3.[ベクトルデータベース、ベクトル検索ライブラリ、ベクトル検索プラグインの比較](https://zilliz.com/learn/comparing-vector-database-vector-search-library-and-vector-search-plugin)
4.[Milvusの紹介](https://zilliz.com/learn/introduction-to-milvus-vector-database)
5.[Milvusクイックスタート](https://zilliz.com/learn/milvus-vector-database-quickstart)
6.[ベクトル類似検索入門](https://zilliz.com/learn/vector-similarity-search)
7.[ベクトルインデックスの基本と反転ファイルインデックス](https://zilliz.com/learn/vector-index)
8.[スカラー量子化と積量子化](https://zilliz.com/learn/scalar-quantization-and-product-quantization)
9.[階層的航行可能小世界(HNSW)](https://zilliz.com/learn/hierarchical-navigable-small-worlds-HNSW)
10.[近似最近傍オーイェー(ANNOY)](https://zilliz.com/learn/approximate-nearest-neighbor-oh-yeah-ANNOY)
11.[プロジェクトに適したベクトルインデックスの選択](https://zilliz.com/learn/choosing-right-vector-index-for-your-project)
12.[DiskANNとVamanaアルゴリズム](https://zilliz.com/learn/DiskANN-and-the-Vamana-Algorithm)

## ご興味のあるウェビナーとイベント

- Zillizウェビナー｜[ベクターデータベース101：クラッシュコース](https://zilliz.com/event/vector-database-101-crash-course)
- Zillizウェビナー｜[HNSW著者Yury Malkovとのファイヤーサイドチャット](https://zilliz.com/event/future-of-vector-search-fireside-chat-yury-hnsw)
- Zilliz Webinar｜[ベクター検索のベストプラクティス](https://zilliz.com/event/vector-search-best-practices)
- Zilliz Webinar｜[Tutorial: Working with LLMs at Scale](https://zilliz.com/event/tutorial-working-llms-at-scale)

article.updateAt

Frank Liu
Frank Liu is the Director of Operations & ML Architect at Zilliz, where he serves as a maintainer for the Towhee open-source project. Prior to Zilliz, Frank co-founded Orion Innovations, an ML-powered indoor positioning startup based in Shanghai and worked as an ML engineer at Yahoo in San Francisco. In his free time, Frank enjoys playing chess, swimming, and powerlifting. Frank holds MS and BS degrees in Electrical Engineering from Stanford University.