学習
自然言語処理（NLP）上級ガイド

データ分析における時系列の埋め込み

Apr 09, 20241 分で読めます

時系列データを予測タスクに適したエンベッディングに変換するための一般的な概念や前処理方法など、時系列データについて学ぶ。

シリーズ全体を読む

時系列は、金融、ヘルスケア、サプライチェーン管理、製造業など、様々なビジネス分野で広く使用されていることから、データサイエンスの基本的なトピックである。この記事では、時系列データに関する全てを説明する。まず、時系列データの一般的な概念について説明する。そして、時系列データを予測タスクに適したエンベッディングに変換するための前処理方法を探ります。それでは、さっそく始めましょう！

時系列データを理解する

時系列データは、規則的な時間間隔（メトリクス）と不規則な時間間隔（イベント）で記録され、時系列に並べられたデータポイントから構成されます。時系列データの特徴は、各データポイントが特定のタイムスタンプに関連付けられていることです：

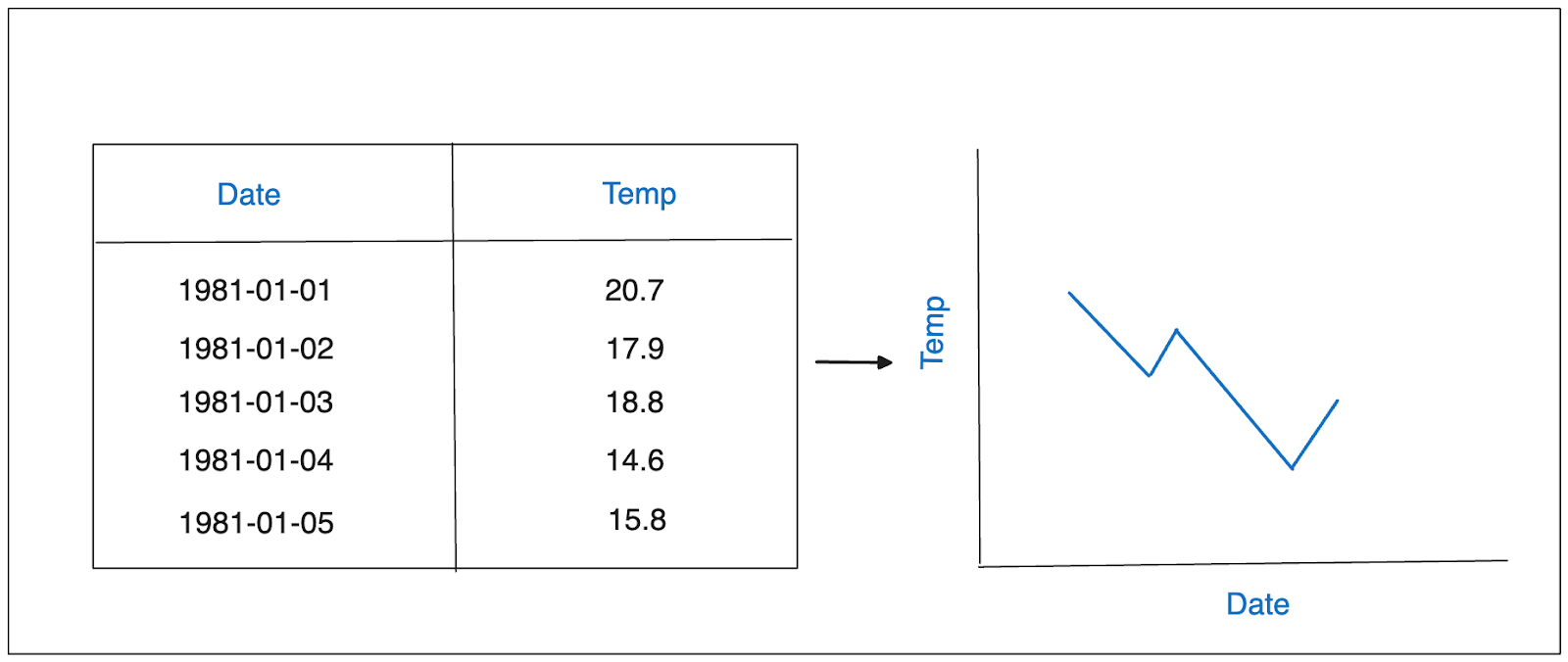時系列データの例.png

例えば、1時間ごとの気温、1ヶ月間の毎日のウェブサイトのトラフィック、風力タービンの1分あたりのブレード回転数を記録したセンサーデータ、小売店の過去1年間の毎月の売上高などである。人々は時系列データを使って過去のパターンを洞察し、将来の戦略的意思決定に役立てている。

時系列データを扱う場合、通常、季節性、傾向性、周期性など、1つ以上のパターンを見つけることができる。

季節性とは、曜日や月などの季節要因によって一定の頻度で変動するデータのパターンを指します。トレンドとは、データの長期的な減少や増加を指す。一方、周期性とは、季節性と似ているが、一定の頻度ではなく、データの変動パターンを指す。

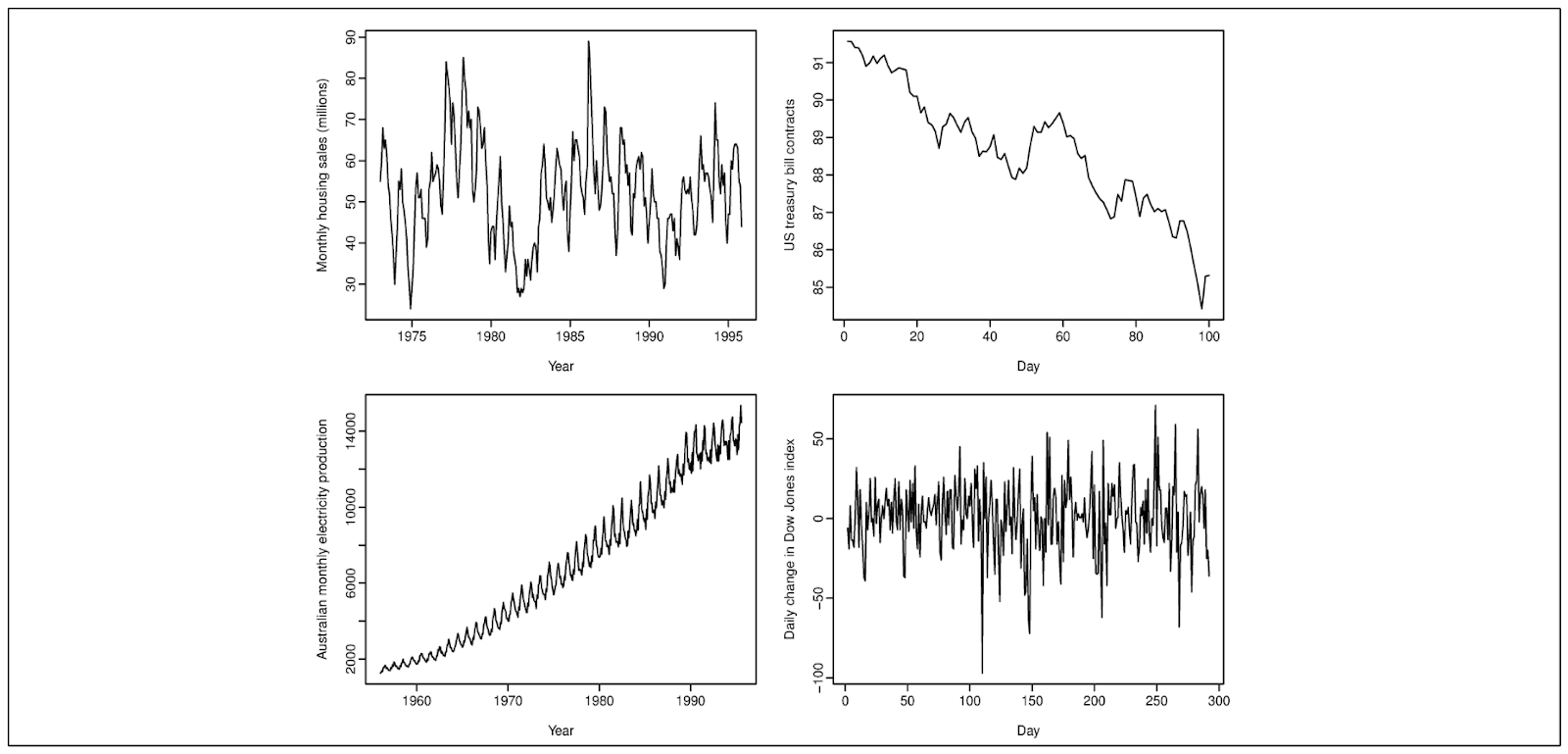左上-季節性右上-減少傾向左下-増加傾向右下-周期性.png

時系列データには2種類ある：

一変量時系列データ:** これは、連続する時間間隔にわたって観測される単一の時間依存変数を含む。一変量時系列データ：***これは、連続する時間間隔にわたって観測される単一の時間依存変数を伴う。
多変量時系列データ：*** これは、同じ時間間隔で記録された複数の時間依存変数を含む。例として、気温を記録するだけでなく、湿度や風速といった他の要素も記録することができる。

時系列予測を理解する

時系列予測は、時系列データセット内の時間に依存する変数の将来の値を予測することを含む。例えば、ある暗号通貨の過去2年間の過去の価格がある場合、今から1週間後の価格を予測したいと思うかもしれない。

時系列予測は単なる理論的な概念ではなく、様々な分野の様々な企業が日常業務で使用する実用的なツールです：

金融機関：** 銀行や投資会社は、株式市場の動向や為替変動を予測したり、顧客の支出パターンの異常を検出したりするために時系列予測を利用している。これはリスク管理戦略の策定に役立つ。
ヘルスケア分野：** 病院やヘルスケアプロバイダーは、患者の入院率を予測し、疾病の蔓延を追跡し、患者のバイタルサインをモニターするために時系列分析を活用している。この強力なツールは、患者のケアと転帰を強化する上で重要な役割を果たしている。
小売業：** 小売業は時系列予測を活用して、販売数量を予測し、顧客の購買行動を分析し、在庫レベルを効率的に管理する。これにより、在庫切れを最小限に抑え、価格戦略を最適化し、全体的な収益性を高めることができます。
モノのインターネット(IoT):** モノのインターネット(IoT)とは、何十億もの接続されたデバイスが常にデータを作成し共有することを指します。サーモスタットやホームハブのようなデバイスがセンサーデータを交換し、誰もいないときに温度を調節したり照明を消したりするようなタスクを自動化する、スマートホームにこれが見られる。このように相互に接続されたセンサー・ネットワークは、IoTデータの時系列分析の重要性を浮き彫りにしている。
製造業:**製造業は、予知保全戦略を採用・改善することで、収益に打撃を与える機械のダウンタイムを削減するため、タイムスタンプ・データを収集・分析する。

時系列予測を行うために、いくつかのモデルを使用することができます。一般的に、時系列予測モデルは統計、機械学習、ディープラーニングの3つに分類される。

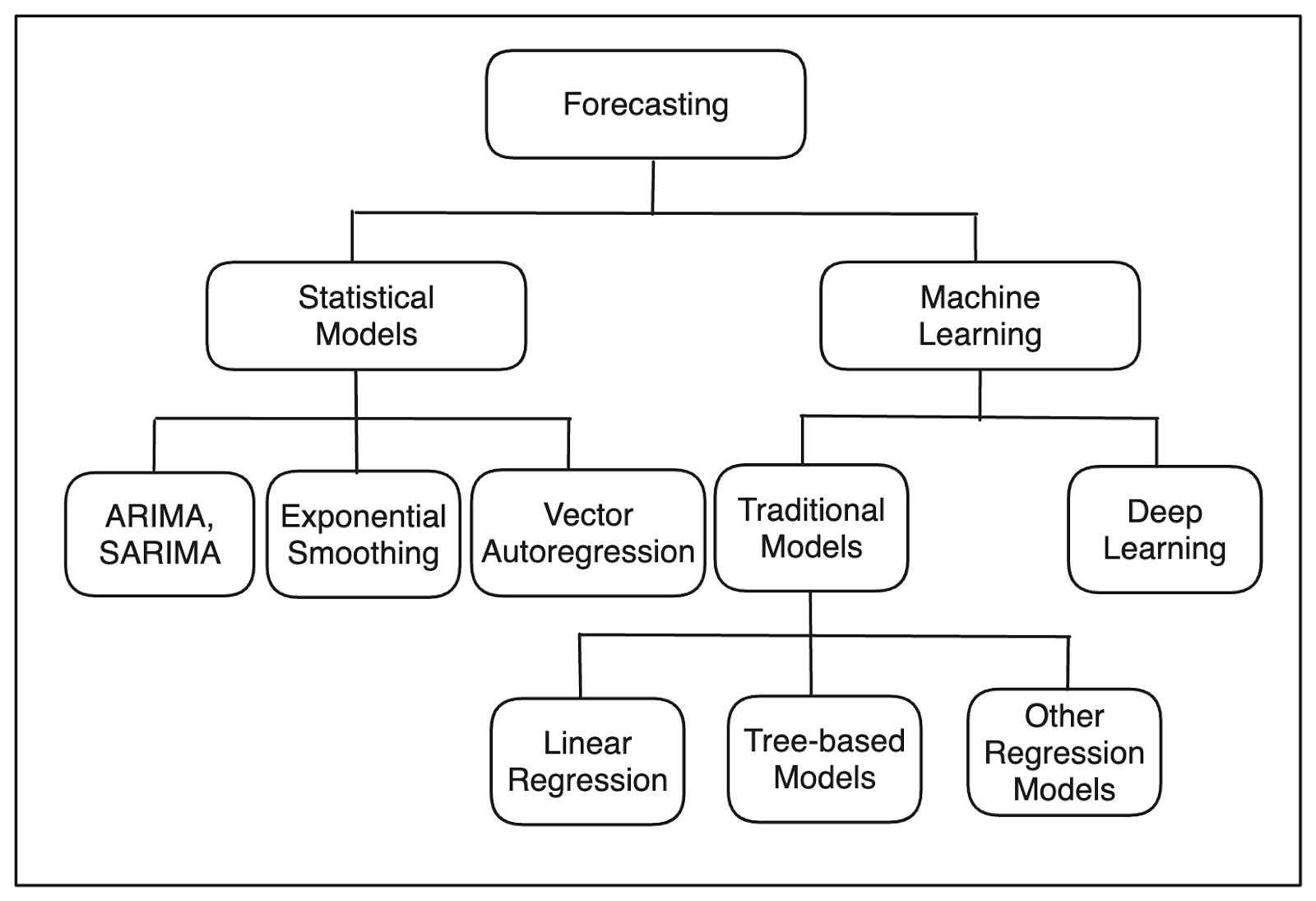時系列予測モデルのカテゴリー.png

統計モデル

統計モデルは、予測のために伝統的な統計的手法を使用します。このカテゴリーのモデルの例としては、ARIMA、SARIMA、指数平滑化、ベクトル自己回帰などがあります。統計モデルは単純で、一変量時系列データの基本的なトレンドや季節性を捉えるには効果的ですが、複雑で非線形なパターンを持つ高次元データでは苦戦することがあります。また、ほとんどの統計モデルは一変量データにしか使えないので、多変量データがある場合は別の方法を探す必要があります。

機械学習モデル

機械学習モデルは、特に複雑で非線形なパターンを持つ高次元時系列データを扱う場合、統計モデルを上回ることが多い。このカテゴリーのモデルの例としては、線形回帰、ランダムフォレスト、勾配ブースティング、その他の回帰アルゴリズムなどがある。

機械学習モデルの利点の1つは、外生データを組み込めることである。外生データとは、予測される変数とは無関係な変数のことである。例えば、気温を予測する場合、外生データには湿度、風速、曜日などが含まれる。外生データを統合することで、モデルの予測力を大幅に高めることができる。

ディープラーニング・モデル

Transformersアーキテクチャの登場以来、ディープラーニングによる時系列予測の進歩も急速に進化している。このカテゴリーのモデルの例としては、LSTM、Informer、Spacetimeformerなどがある。複雑で非線形な関係を持つ巨大な時系列データに対して、深層学習モデルは機械学習や統計モデルと比較して優れたパフォーマンスを提供する可能性がある。

しかし、時系列予測にディープラーニング・モデルを使用することの欠点は、解釈可能性の欠如である。ディープラーニング・モデルのアーキテクチャは非常に複雑であるため、通常はブラックボックスとして扱われる。時系列予測では解釈可能性が重要であることが多いため、これは問題となる。

予測のための時系列埋め込み

単純なパターンを持つ一変量時系列データでは、データをそのまま受け取り、統計モデルを使って時系列予測を行うことができる。しかし、複雑な一変量データや多変量データに対して機械学習やディープラーニングのような高度な手法を使いたい場合は、さらに前処理を行う必要がある。

機械学習モデルは、各行が1つの観測を表し、各列が特徴を表す行列の形でデータが構造化されていることを期待する。

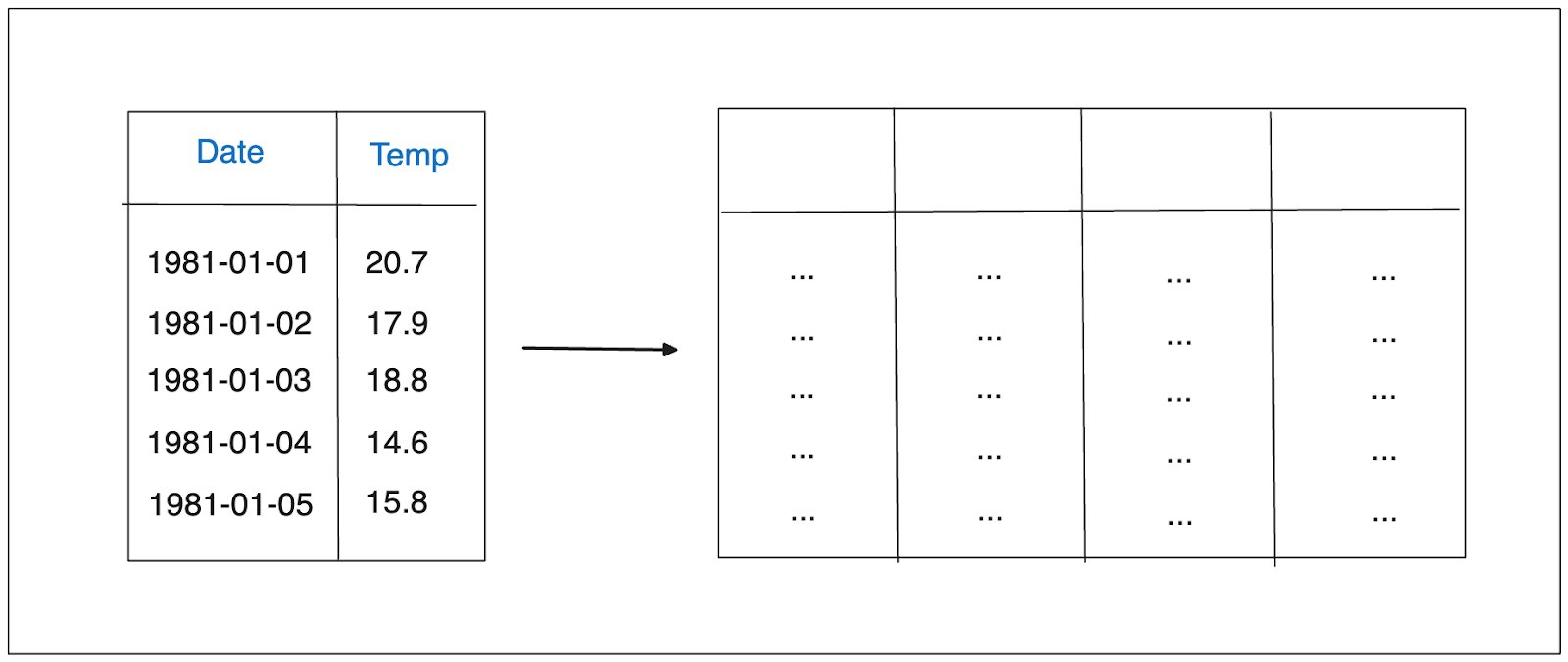時系列エンベッディングの図.png

問題は、どのようにして時系列データを機械学習モデルが期待する行列形式に変換するかということだ。ラグ特徴、窓特徴、外生特徴の追加など、いくつかの方法があります。

ラグ特徴による時系列埋め込み

ラグ特徴のコンセプトは非常にシンプルで、n個前の時間ステップからの観測を特徴として取り込みます。言い換えれば、n個の時間ステップでデータをシフトさせるということである。

例として、ラグ値を1、2、3とする。下図のような日ごとの気温データがあるとすると、データの変換は次のようになる：

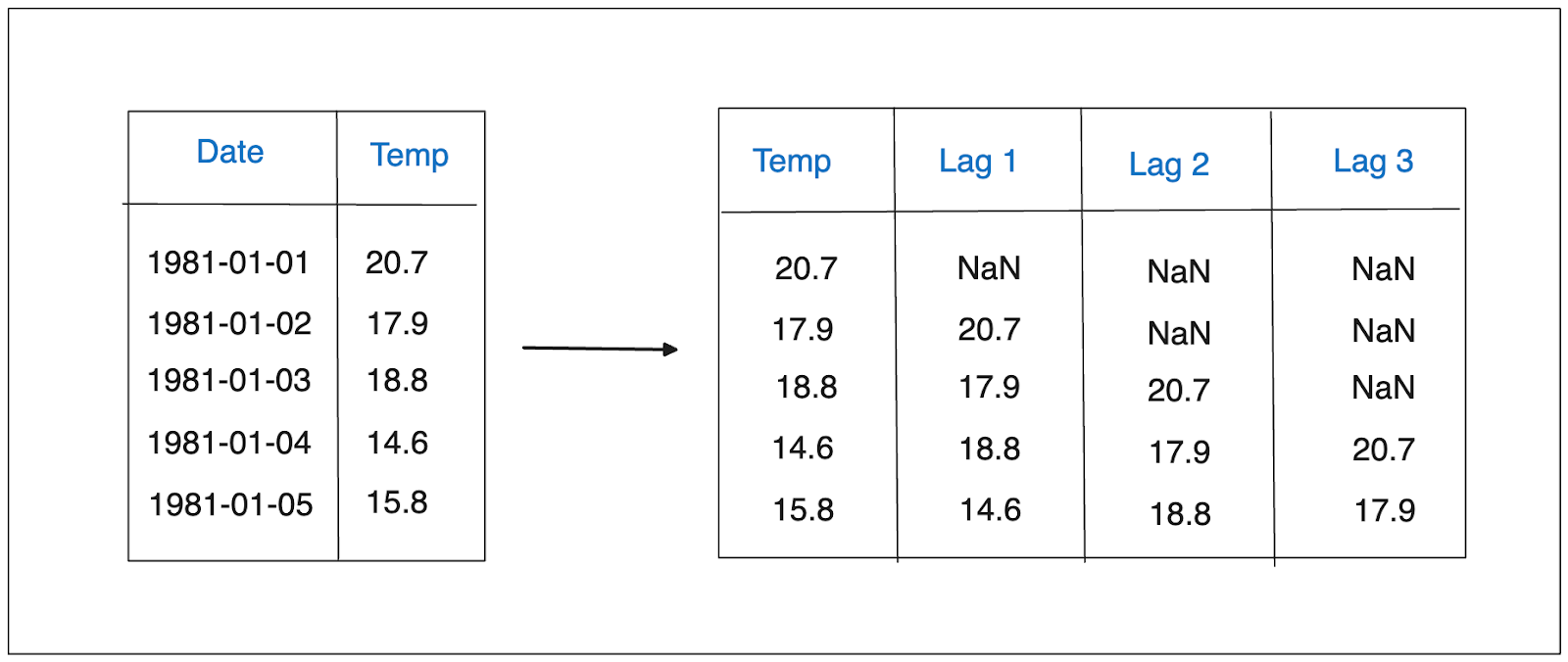ラグ特徴.png

上記の可視化において、t-1は現在の気温の1日前の気温、t-2は現在の気温の2日前の気温、t-3は現在の気温の3日前の気温を表している。時系列データのパターンに対する洞察を提供するため、ラグ特徴を前処理として追加することは、我々の機械学習モデルにとって必要である。

窓特徴による時系列埋め込み

ラグ特徴に加えて、過去の n 個のオブザベーションの集合の要約統計量を使い、それらを特徴として含めることで、時系列データを行列に変換することもできます。要約統計量は、平均値や中央値など何でもかまいません。しかし、平均値が窓特徴としてよく使われます。

例として、毎日の気温データで窓特徴を実装したいので、窓値を2に設定するとします。この場合、今日の気温を予測するための特徴量の一部として、過去2日間の平均値を使用します。

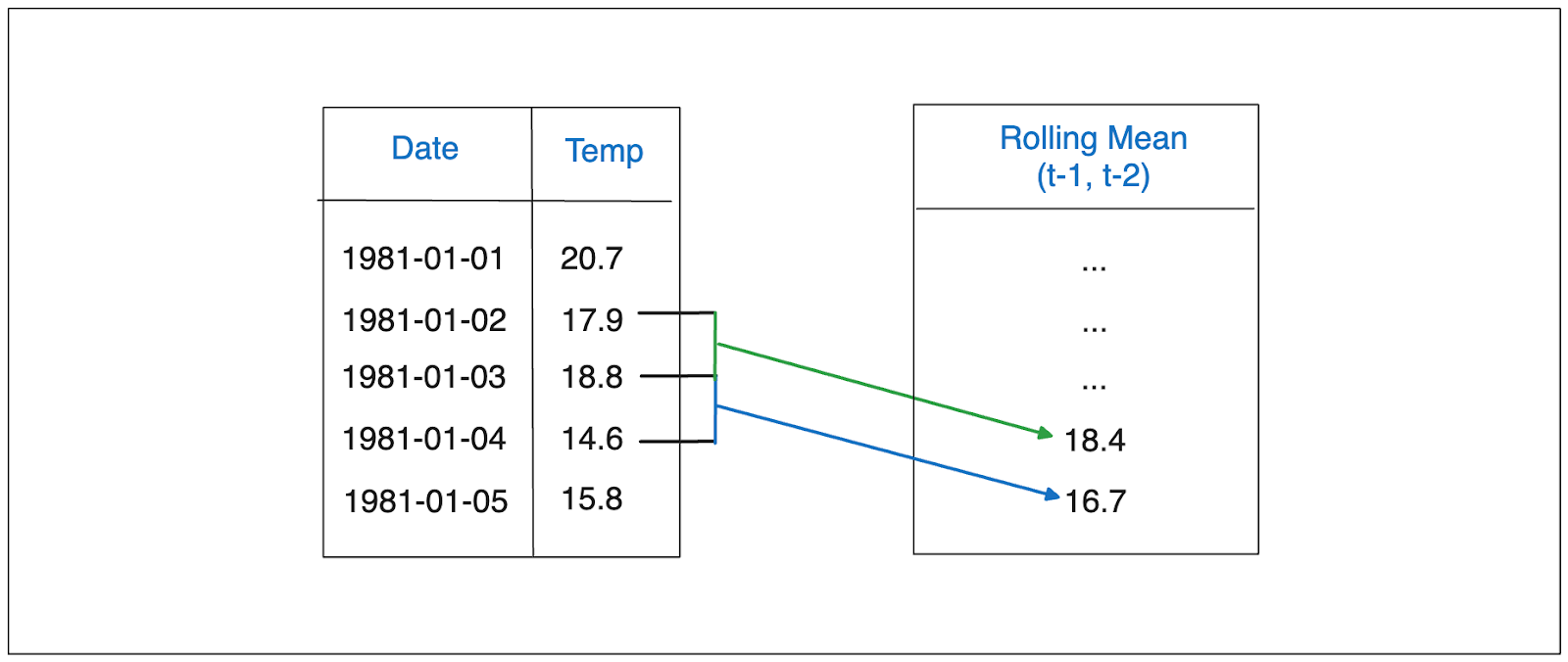窓の特徴.png

窓の特徴は、時系列データの局所的なトレンドや変動に関する洞察を提供するため、学習中の機械学習モデルにとって重要な役割を果たします。これらの特徴は、時系列データが非定常である場合に非常に有用です。

外生特徴による時系列埋め込み

外生的特徴とは、予測したい変数とは直接関係のない特徴を指します。気温データの文脈では、外生特徴には曜日、湿度、風速、年の四半期などが含まれます。

しかし、外生的特徴を取り入れる際には注意が必要です。特定の時間ステップにおける変数の値を予測したい場合、その時点ですべての特徴の値がわかっていなければなりません。湿度や風速のような特徴がある場合、予測時点ではこれらの特徴の値を持っていない可能性があります。

したがって、経験則として、常に自問自答してください：予測を行う必要がある時点までに、ある特徴の値に関する情報を持っているだろうか？もしそうであれば、時系列エンベッディングの一部としてこの特徴を追加することができます。

時系列予測の実装

このセクションでは、時系列予測タスクを実装します。その過程で、前節で述べた全てのテクニックを使って、データをエンベッディングに変換します。

データセット](https://raw.githubusercontent.com/jbrownlee/Datasets/master/daily-min-temperatures.csv)では、オーストラリアのメルボルンで記録された1981年から1990年までの10年間の最低気温データを使います。データを埋め込みデータに変換し、回帰モデルを学習するには、scikit-learnのような一般的な機械学習ライブラリを利用します。必要なライブラリとデータをロードしよう。

np として numpy をインポートします。
import matplotlib.pyplot as plt
import pandas as pd

from sklearn.ensemble import RandomForestRegressor
from sklearn.linear_model import Lasso
from sklearn.metrics import mean_squared_error

# 毎日の最低気温データ
url = "<https://raw.githubusercontent.com/jbrownlee/Datasets/master/daily-min-temperatures.csv>"
df = pd.read_csv(url)

df["Date"] = df["Date"].apply(lambda x: pd.to_datetime(x))
df = df.set_index("Date")
df.head()

入力データ.png

1981年から1990年までの一変量の気温データがある。しかし、予測タスクのために機械学習モデルを訓練したい場合、このデータをそのまま使うことはできない。データの傾向や季節性を捉え、モデルの性能を向上させるために、データをエンベッディングに変換する必要があります。

データを埋め込むために、ラグ特徴、窓特徴、外生特徴を組み合わせて実装しよう。ラグ特徴では、ラグ値を1と7に設定します。窓特徴では、過去14日間の気温の平均と標準偏差を計算する。外生的特徴については、月、年、四半期を記録する。その後、null 値の行をすべて削除する。

# ラグ特徴量、値を1と7に設定
df[f "y_lag_1"] = df["Temp"].shift(periods=1)
df[f "y_lag_7"] = df["Temp"].shift(periods=7)

# ウィンドウの特徴量、値を14に設定する
result = (
    df["Temp"]
    .rolling(window=14)
    .agg(["mean", "std"])
    .shift(periods=1)
)

result = result.add_prefix("y_window_14")
df = df.merge(result, how="left", left_index=True, right_index=True)

# 月、年、四半期を取得する。
df["month"] = df.index.month
df["year"] = df.index.year
df["quarter"] = df.index.quarter

# ヌル値を削除
df.dropna(inplace=True)

# ラベルに温度を設定
y = df["Temp"].
X = df.drop("Temp", axis=1)

最終特徴埋め込み.png

これで時系列データは埋め込みデータに変換されました！これで、これらの埋め込みを回帰モデルの入力として使うことができます。

学習プロセス前の最後のステップは、データを学習セットとテストセットに分割することです。そのために、最初の9年間のデータをトレーニング・データとして使い、最後の1年間をテスト・データとして使います。そして、回帰モデルをインスタンス化して、訓練データを使って訓練します。

end_train ='1990-01-01'

X_train = X.loc[:end_train].
X_test = X.loc[end_train:]です。

y_train = y.loc[:end_train]。
y_test = y.loc[end_train:]。

# モデルをインスタンス化してトレーニングする
lasso = Lasso(random_state=9)
lasso.fit(X_train, y_train)

モデルの学習が完了したので、テストデータに対して時系列予測を行い、予測結果と実際の気温値を比較してみましょう。下記は予測結果のデータ可視化です。

# テストデータに対する気温予測
preds = lasso.predict(X_test)
preds = pd.Series(preds, index=X_test.index)

# 予測結果と実際の結果をプロット
fig, ax = plt.subplots(figsize=(12, 8))
y_train[-200:].plot(ax=ax, label='train')
y_test[:200].plot(ax=ax, label='test')
preds.iloc[:200].plot(ax=ax, label='predictions')
ax.legend(bbox_to_anchor=(1.3, 1.0))

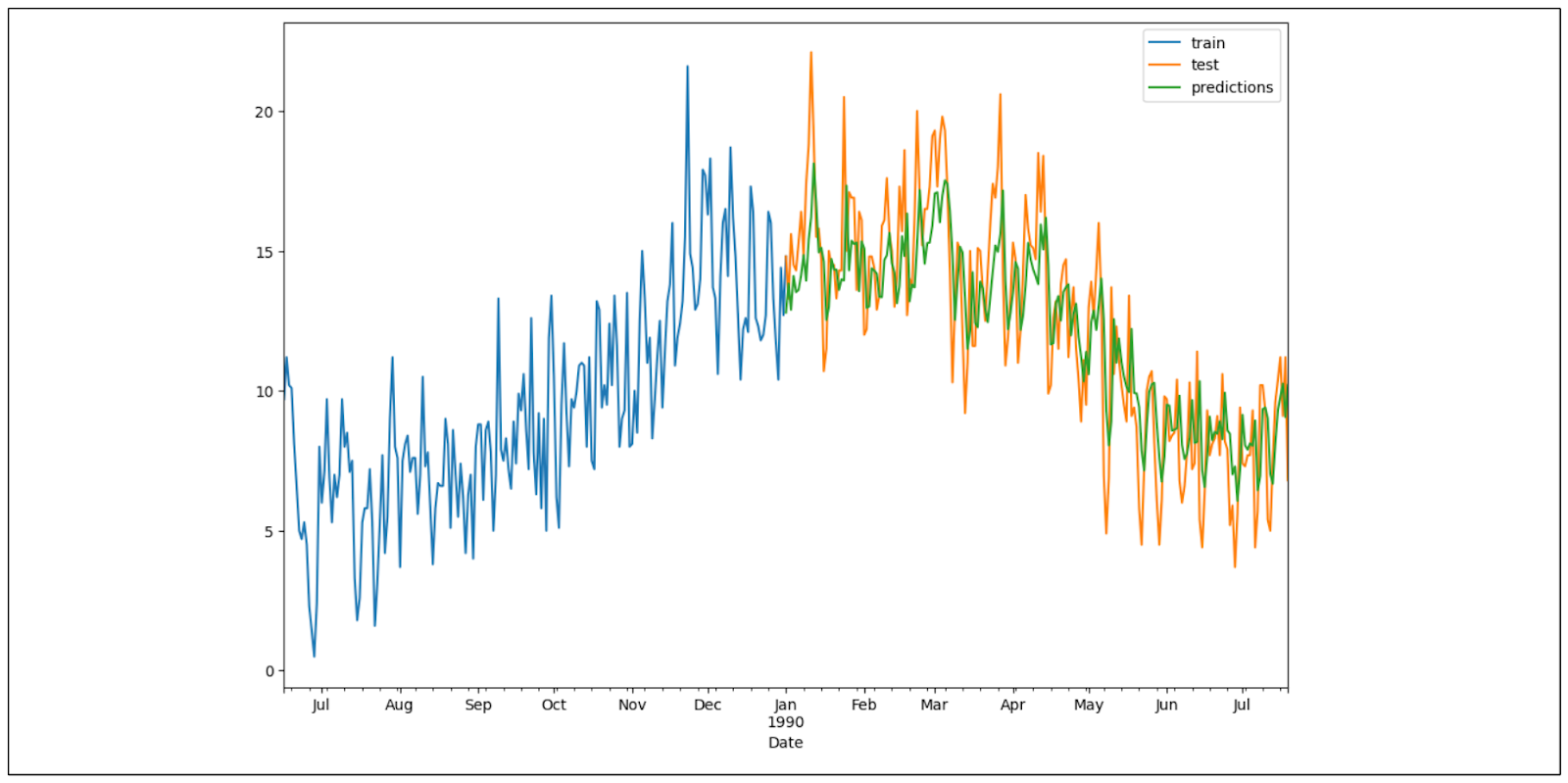時系列予測結果.png

ご覧のように、我々のモデルの予測結果は、テストデータのトレンドと季節性を捉えることができ、非常に良好です。機械学習モデルのパフォーマンスを微調整するために、ラグ、窓、外生特徴を試すことができます。

結論

時系列データは、特定の時間間隔にわたって記録された一連の観測から成り、季節性、トレンド性、周期性といった1つ以上のパターンを示すことがある。機械学習のような高度な手法を使ってこのデータを予測するためには、ラグ、窓、または外生特徴を導入することで埋め込みに変換する必要がある。これらの特徴は、時系列データの季節性、トレンド性、周期性を効果的に捉えることができるため、機械学習モデルにおいて重要な役割を果たします。各特徴の値は、データのユニークな特徴とドメイン知識を考慮して、細心の注意を払って微調整する必要があることに注意することが重要である。

article.updateAt