学習
自然言語処理（NLP）上級ガイド

データの合理化次元を減らす効果的な戦略

Apr 03, 20241 分で読めます

この記事では、データが多すぎることが機械学習モデルのパフォーマンスをどのように阻害するのか、そしてこの問題に対処するために何ができるのかについて説明する。

シリーズ全体を読む

データ・サイエンスの実務者であれば、機械学習モデルをトレーニングする際の経験則として、「データが多ければ多いほど、モデルの性能は向上する」という話を聞いたことがあるかもしれない。しかし、この法則がすべてのシナリオで当てはまるとは限りません。

この記事では、データが多すぎると機械学習モデルのパフォーマンスが低下する可能性があること、そしてこの問題に対処するために何ができるかを説明します。

それでは、早速始めましょう！

次元の呪い

データが多すぎることの問題を議論する前に、次元の概念を理解することが重要です。

データサイエンスでは、次元とはデータセットに含まれる入力変数や特徴の数を指す。例えば、住宅データセットでは、住宅価格、ベッドルーム数、バスルーム数、床面積、住所、建築年、室内設備などがディメンションに含まれる。

機械学習モデルに次元を追加すれば、性能が向上すると考えるかもしれない。しかし、多くの場合その逆である。なぜなら、データの次元を増やせば増やすほど、スパースになるからだ。線（1次元）を想像してみてほしい。その空間を数点のデータで埋めるのは比較的簡単だ。矩形（2D）の場合、その面積をカバーするためにはより多くのデータポイントが必要になる。立方体（3D）を考えると、それを埋めるにはさらに多くのデータポイントが必要になる。

画像は著者による](https://assets.zilliz.com/Image_by_author_c68540459b.png)

n次元空間でデータが埋める必要のある空間を特徴空間と呼ぶことができる。次元が高ければ高いほど、特徴空間は大きくなり、データから意味のある情報を抽出するためには、より多くのデータポイントが必要になります。

高次元化はいくつかの問題を引き起こす：

計算資源：計算資源：次元が大きくなると、データ処理に必要な計算資源が増える。
データのスパース性**：特徴空間が拡大するにつれ、データポイントが分散し、機械学習モデルのクラスタリングや分類タスクが複雑になる可能性が高い。
モデルのパフォーマンス低下特徴空間が大きくなると、KNNやk-meansクラスタリングのような距離メトリクスに依存するアルゴリズムのパフォーマンスが低下する可能性があります。さらに、過剰な次元は、モデルがデータにフィットしすぎて、未知のデータポイントに汎化するのに苦労するオーバーフィッティングにつながる可能性があります。
可視化の難しさ高次元データの可視化は困難であり、分析や解釈を難しくする。

上記の問題は、人々が "次元の呪い "と呼ぶものである。

では、どのようにすれば次元の呪いを軽減し、データ本来の次元を得ることができるのでしょうか？この問題に対処する方法はいくつかあるので、次のセクションでそれを探ろう。

次元削減アルゴリズム

次元の呪いの問題に対処するために、データサイエンスではいくつかの一般的な次元削減手法が適用される。これらのアルゴリズムには、主成分分析（PCA）、t-Distributed Stochastic Neighbor Embedding（t-SNE）、Uniform Manifold Approximation and Projection（UMAP）などがあります。

主成分分析(PCA)

PCAは、おそらく最もよく知られている次元削減手法の1つです。要するに、PCAは最大分散を保つ軸にデータを投影する。しかし、これは何を意味するのでしょうか？次のような2次元特徴空間のデータ点の例を考えてみよう。

画像は著者による](https://assets.zilliz.com/scatter_plot_44212dc91f.png)

左：2次元散布図、右：PCAの主成分。

データ分析と機械学習において重要なツールであるPCAは、次元を1次元（直線）に減らすために使用できる。まずPCAは、データ点から最も多くの情報を保持する軸を見つけ、データを1次元に投影する際に重要な情報を確実に保持することを目指す。上の右側のビジュアライゼーションからわかるように、長いベクトルは、短いベクトルと比較して、データから最も多くの情報を保持する射影を表します。

PCAは、最も情報を保持する射影を選択します。したがって、PCAは長いほうのベクトルを第1軸として選択する。次に、最初の射影に直交し、データから2番目に多くの情報を保持する2番目の軸を特定します。

上の2次元特徴空間の例では、2番目の軸は、上の可視化でより短いベクトルと一致します。PCAは、3Dまたは高次元の特徴空間があれば、3番目の軸も識別します。

PCAアルゴリズムによって選択された軸は、主成分として知られています。すべての主成分が決定されると、PCAは下図のように特徴空間を低次元に射影します。

画像は著者による](https://assets.zilliz.com/principal_components_of_PCA_7024e7e083.png)

*左：PCAの主成分、右：PCAによる最終的な投影結果。

t-分布確率的近傍埋め込み(t-SNE)

非線形に分離可能なデータ点を含むデータセットを扱う場合、PCAでは良い結果が得られないことがある。下の可視化に示すように、3次元空間のスイスロールデータセットを考えてみよう。異なるクラスのデータ点が特徴空間全体に散らばっている。このような場合、下の画像の右側に示されているように、線形PCAは意味のある射影を提供しないかもしれません。

著者による画像](https://assets.zilliz.com/swiss_roll_3_D_data_points_b2c7308998.png)

左：スイスロール3次元データ点、右：PCAによる2次元射影結果。

非線形に分離可能なデータ点を扱う場合、投影ベースのアルゴリズムは最良の解決策とはならないかもしれない。そこで、t-SNEのような多様体ベースのアルゴリズムが活躍する。

t-SNEは、2002年に発表されたオリジナルのSNEアルゴリズムの改良版である。t-SNEの「t」は、低次元空間における各データ点間の類似度を計算するために、正規ガウス分布の代わりにt分布を使用することを示している。

t分布の特徴の一つは、ガウス分布よりも重い尾を持つことである。この特徴により、t-SNEアルゴリズムは、より疎な距離で異なるクラスタを可視化することができる。

例えば、2次元特徴空間に散在するデータポイントがあり、その次元を1次元に縮小したいとします。

画像は著者による](https://assets.zilliz.com/scatter_points_0aedb88b52.png)

左：2次元散布点、右：近傍点の類似性を見つけるためのデータ点を中心とした分布。

各データ点xiについて、アルゴリズムはxiを中心とするガウス分布を用いて各近傍点xjの類似度を推定する。このステップの結果は各隣接点の確率であり、我々はこれをPijと呼ぶ。

xi_を中心とするガウス分布の分散は、xi近傍のデータ点の密度に依存します。このパラメータはt-SNEではperplexityと呼ばれることが多い。データ点の周りの密度が高ければ高いほど、当惑度は高くなる。各データ点の周りの密度が変化することを考えると、異なるデータ点に対して異なる分散を持つ分布が得られる可能性がある。

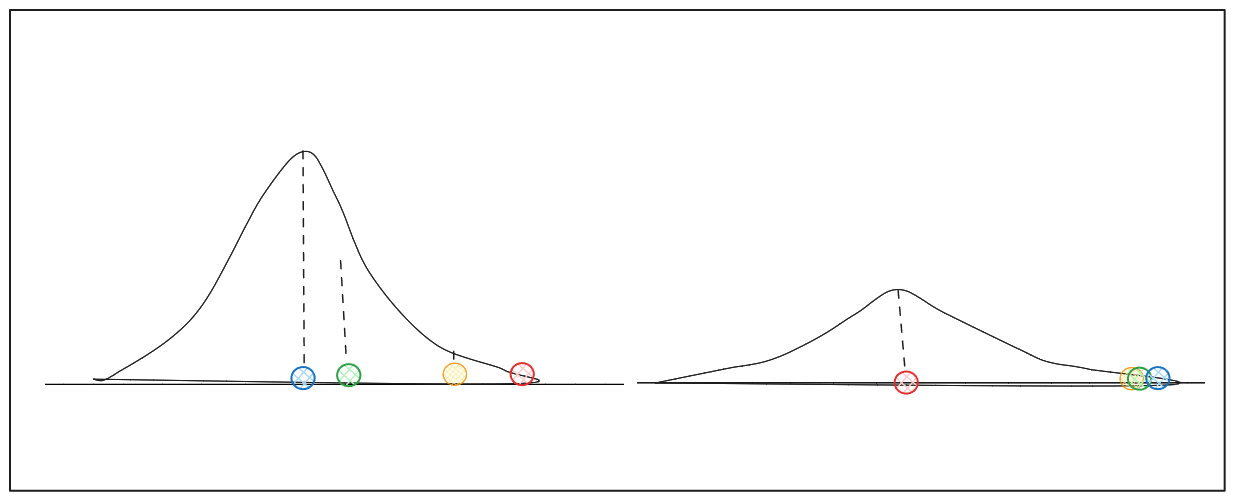著者による画像(異なる分散を持つ分布.png)

密度の多様性により、アルゴリズムはxiとその近傍間の類似度を正規化し、類似度の合計が1になるようにする。

次のステップでは、アルゴリズムは、Pijによく似た低次元空間Qijの確率を見つけることを目的とする。Pij_とQijの類似度を測定するために、t-SNEは、次式で表されるKL（Kullback-Leibler）発散を用いる：

を用いる。$$

このKLダイバージェンス方程式は、回帰アルゴリズムの最適化に使用されるものと同様の勾配降下アルゴリズムを用いて最適化される。

一様多様体近似と射影(UMAP)

t-SNEは一般的に複雑なデータポイントの処理に優れていますが、このアルゴリズムを実行するために必要な計算リソースは、特に大規模なデータセットではかなり高くなる可能性があります。これは各データ点のペアワイズ類似度を計算する必要があるためである。UMAPは、非線形分離可能で複雑なデータ点を管理するための、t-SNEに代わる実行可能なアルゴリズムである。

高レベルでは、UMAPはt-SNEと同様に動作する。UMAPは最適化手法を用いてデータの高次元表現を低次元表現に変換する。

UMAPは、高次元空間のデータ構造を特定するためにグラフベースのアルゴリズムを使用する。具体的には、ファジー単純複合体アルゴリズムを利用する。グラフアルゴリズムに馴染みのある方なら、これは基本的に重み付けされた辺を持つグラフである。重みは2つのデータ点がつながっている可能性を示す。

下図のような2次元散布図を考えてみよう：

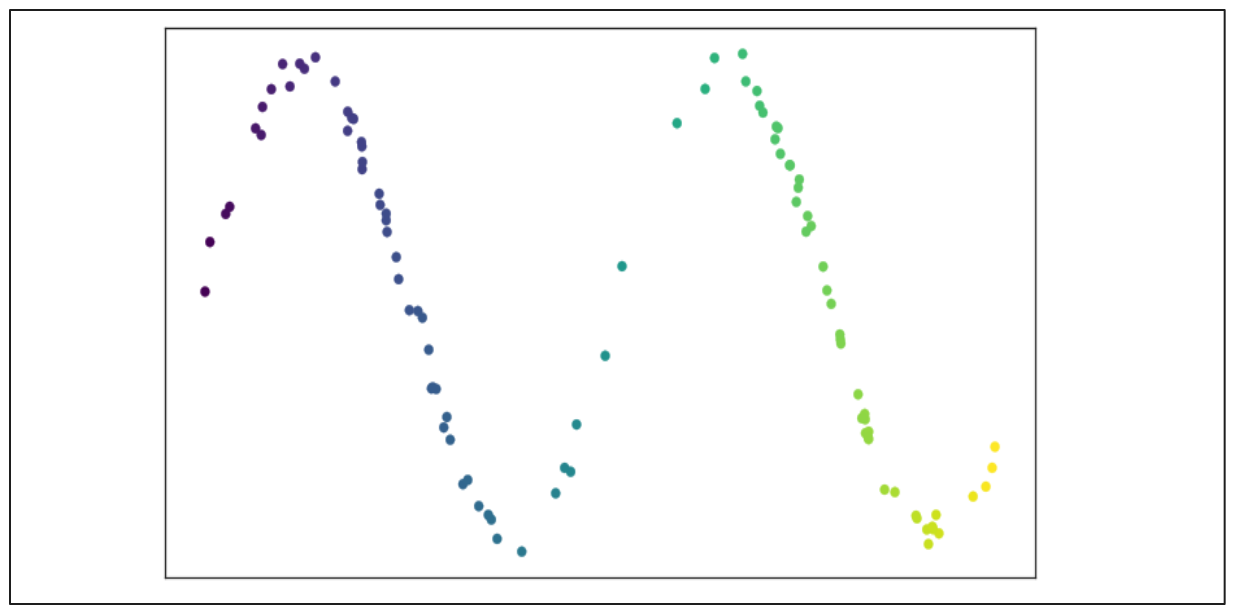
画像ソースUMAPドキュメント

これらのデータ点からグラフを構築するために、まず各データ点が考慮すべき最近接点(n)を指定する。次に、UMAPはn番目の最近接点までの距離に基づいて、各点から半径を外側に広げる。半径が重なればデータ点はその近傍に接続される。

しかし、半径が広がるにつれて接続の可能性（エッジの重み）は減少する。この方法は、各データ点が少なくとも1つの最近傍に接続されていることを保証する。高次元空間の大域構造と低次元空間の局所構造のバランスを保つ。

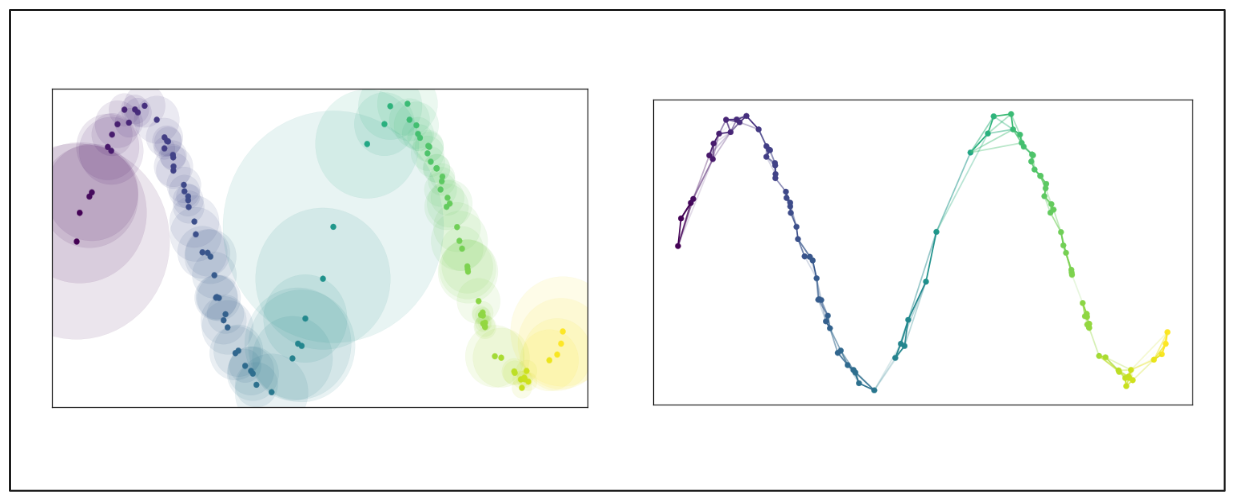
画像ソースUMAPドキュメント

高次元空間のグラフが構築されると、このアルゴリズムは、t-SNEに似た最適化関数によって、このレイアウトを低次元空間で再現し、可能な限り類似させることを目指す。

UMAPとt-SNEの最も顕著な違いの一つは、大域構造と局所構造のバランスである。ほとんどの場合、UMAPの方が、低次元空間への最終的な投影において、データの大域的な構造を保持することに優れている。これは、クラスタ間の関係がt-SNEよりも意味があることを意味する。

次元削減の実装

このセクションでは、前のセクションで説明した3つのアルゴリズムを使って、MNIST手書き数字データセットの次元削減を行います。そのために、一般的な機械学習ライブラリであるScikit-learnを利用します。まず手書き数字データを読み込みましょう。


!pip install umap-learn import seaborn as sns from umap import UMAP from sklearn.decomposition import PCA from sklearn.manifold import TSNE from sklearn.datasets import fetch_openml sns.set(style='white', rc={'figure.figsize':(12,8)})# Fetch data mnist = fetch_openml('mnist_784') data = mnist.data labels = mnist.target	.

画像ソースウィキペディア

我々のデータセットは、0から9までの手書き数字の画像で構成されており、合計70,000枚の画像がある。各画像は28×28ピクセルの行列を平坦化したもので、784次元になる。したがって、我々のデータの形状は (70,000, 784) である。

PCAとt-SNEはScikit-learnライブラリを使って初期化できますが、UMAPはScikit-learnをベースに作られたスタンドアロンライブラリから初期化する必要があります。各アルゴリズムのパラメータとして、ライブラリのデフォルト値を使用する。次に、各アルゴリズムをデータにフィットさせ、次元削減を適用する。


embeddings = { "PCA embedding"：PCA( n_components=2, random_state=0 ), "t-SNE embedding"：TSNE( n_components=2, random_state=0 ), "UMAP embedding"：UMAP( n_components=2, random_state=0 ) } projections = {}.for name, transformer in embeddings.items(): print(f'Computing {name}...') projections[name] = transformer.fit_transform(data)	.

著者による画像](https://assets.zilliz.com/PCA_8adeb8be33.png)

上の可視化からわかるように、PCAの次元削減は、データから意味のある情報を取り出すには不十分です。これは、PCAが投影アルゴリズムであり、データが線形分離可能なときに最もよく機能することから理解できる。最初のいくつかの主成分は、データの分散を説明できる。しかし、我々のMNISTデータセットの場合はそうではない。

一方、t-SNEとUMAPの結果は非常に良い。異なるクラスに属するデータポイントによって形成される明確なクラスタを観察することができる。UMAPによって形成されたクラスターはt-SNEによるクラスターよりも若干良好で、誤ったクラスターに配置された桁数が少ない。実行時間の観点からも、t-SNEはデータ点数が増えるにつれて計算量が増えるため、UMAPはt-SNEを上回る。

次元削減アルゴリズムの応用例

データの可視化に非常に有用であることに加え、この記事で取り上げたすべての次元削減アルゴリズムは、さまざまな使用ケースにわたってさまざまな利点を提供します：

自然言語処理**](https://zilliz.com/learn/A-Beginner-Guide-to-Natural-Language-Processing) (NLP)タスク：これらのアルゴリズムは、大規模なテキストコーパスから単語の埋め込みを可視化し、意味的に類似した単語の識別を容易にすることができる。
クラスタリングと分類タスク**：低次元空間におけるデータポイントのセグメントやクラスターを作成し、データ内のパターンや傾向の識別を容易にします。
異常検出**：これらのアルゴリズムはデータの異常値を識別し、データ分析中に適切に対処できるようにします。
コンピュータビジョン画像や動画データの圧縮を支援し、重要な情報を失うことなく効率的なデータ保存を実現します。
特徴選択と特徴工学**：これらのアルゴリズムは、冗長な特徴を除去し、機械学習モデルのパフォーマンスと解釈可能性を向上させます。

結論

データ中に特徴が多すぎると、特徴空間が過度に大きくなる「次元の呪い」問題が発生する。これは、データの疎らさ、モデルの性能低下、データの解釈の困難さなど、いくつかの問題を引き起こす。次元削減アルゴリズムは、データの大域的な構造を保持しながら、データを低次元空間に投影することで、これらの問題に対処します。

PCAは、データポイントが線形分離可能で、最初の数個の主成分でデータの分散を説明できる場合に優れた結果をもたらします。より複雑なデータ点に対しては、t-SNEとUMAPがより良い選択となる。しかし、多数のデータ点を扱う場合は、t-SNEに比べて計算効率が優れているUMAPが望ましい。

この記事が、あなたが次元削減の概念を始めるのに役立つことを願っています。よい学習を！

article.updateAt