スカラー量子化と積量子化
前回のチュートリアル](https://zilliz.com/learn/vector-index)では、最も基本的なインデックス作成アルゴリズムの2つ、フラットインデックスとインバーテッドファイル(IVF)を取り上げました。フラットインデキシングは最も単純で素朴なベクトル検索戦略ですが、データセットサイズが小さい場合（数千ベクトル）、および/またはクエリにGPUを使用している場合、驚くほどうまく機能します。一方、IVFは、他のインデックス戦略ともうまく連携しながら、高度に拡張可能です。
このチュートリアルでは、量子化技術、特にスカラー量子化（整数量子化とも呼ばれる）と積量子化について深く掘り下げることで、その知識の上に構築していきます。Pythonで独自のスカラー量子化アルゴリズムと積量子化アルゴリズムを実装します。
量子化と次元削減の比較
以前のベクトル類似度探索のチュートリアルで述べたように、量子化はベクトルの全体的な精度を下げることでデータベースの総サイズを小さくするテクニックです。これは、ベクトルの長さを削減する次元削減（PCA、LDAなど）とは大きく異なることに注意してください：
python
vector.size # 元のベクトルの長さ 128 quantized_vector.size # 量子化されたベクトルの長さ 128 reduced_vector.size # 量子化したベクトルの長さ 16
PCAのような**次元削減**手法は、線形代数を使って入力データを低次元の空間に投影します。ここではあまり深く考えずに、これらの方法は一般的に、データの分布に制限があるため、主なインデックス作成戦略としては使用されないということだけ知っておいてください。例えばPCAは、独立したガウス分布成分に分離できるデータに最もよく機能する。
一方、**量子化** は、データの分布について何の仮定もしません - むしろ、各次元（または次元のグループ）を個別に見て、各値を多数の離散バケットのいずれかに「ビン詰め」しようとします。元のベクトルすべてに対してフラットサーチを実行する代わりに、量子化されたベクトルに対してフラットサーチを実行することができます。
## スカラー量子化
スカラー量子化は、浮動小数点値を低次元の整数に変換する重要なデータ圧縮技術です。 例を見てみましょう：
例を見てみよう。
>>> vector.dtype # 元のベクトルのデータ型
dtype('float64')
>> 量子化_ベクトル.dtype
dtype('int8')
>> reduced_vector.dtype
dtype('float64')
上の例から、スカラー量子化によってベクトル（とベクトル・データベース）の合計サイズがなんと8倍も小さくなったことがわかる。素晴らしい。
スカラー量子化の仕組み
スカラー量子化は具体的にどのように機能するのでしょうか？まず、インデックス作成プロセス、つまり浮動小数点ベクトルを整数ベクトルに変換するプロセスを見てみましょう。各ベクトル次元について、スカラー量子化はデータベース全体で見たその特定の次元の最大値と最小値を取り、その次元をその範囲全体にわたって一様にビンに分割します。
これをコードで書いてみよう。まず、多変量分布からサンプリングされた1,000個の128D浮動小数点ベクトルからなるデータセットを生成します。これはおもちゃの例なので、ガウス分布からサンプリングすることにします。実際には、（変分オートエンコーダのように）モデルの学習時に制約として追加されない限り、実際の埋め込みがガウス分布になることはほとんどありません：
python
np として numpy をインポートする。 dataset = np.random.normal(size=(1000, 128))
このデータセットは、スカラー量子化の実装で使用するダミーデータの役割を果たします。次に、ベクトルの各次元の最大値と最小値を決定し、それを `ranges` という行列に格納しよう：
``python
>> ranges = np.vstack((np.min(dataset, axis=0), np.max(dataset, axis=0)))
入力データはゼロ平均の単位分散ガウシアンからサンプリングされているので、このおもちゃの例では、ここでの 最小値 と 最大値 はすべての次元にわたってかなり均一であることに気づくだろう。これで、データセット全体の各ベクトル次元の最小値と最大値がわかった。これで、各次元の「開始値」と「ステップサイズ」を決めることができる。開始値は単純に最小値で、ステップ・サイズは使用する整数型の離散ビンの数で決まります。この場合、8ビットの符号なし整数 uint8_t を使用し、合計256ビンとする：
python
starts = ranges[0,:] >> steps = (ranges[0,:])
ステップ = (ranges[1,:] - ranges[0,:]) / 255
必要な設定はこれだけだ。実際の量子化は、各次元のすべての開始値（`starts`）を引き、結果の値をステップサイズ（`steps`）で割ることで行われる：
python
>> dataset_quantized = np.uint8((dataset - starts) / steps)
>> dataset_quantized
array([[136, 58, 156, ..., 153, 182, 30]、
[210, 66, 175, ..., 68, 146, 33],
[100, 136, 148, ..., 142, 86, 108],
...,
[133, 146, 146, ..., 137, 209, 144],
[ 63, 131, 96, ..., 174, 174, 105],
[159, 78, 204, ..., 95, 87, 146]], dtype=uint8)
量子化されたデータセットの 最小値 と 最大値 をチェックすることもできる：
python
np.min(dataset_quantized, axis=0) array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0、 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], dtype=uint8) np.max(dataset_quantized, axis=1) array([255, 255, 255, 255, 255, 255, 255, 255, 254, 254, 255、 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 254, 255, 255, 255, 255, 254, 255, 255, 254, 254, 255, 255, 254, 255, 255, 255, 254, 255, 255, 255, 255, 255, 255, 255, 255, 255, 254, 255, 255, 255, 255, 255, 254, 255, 255, 255, 254, 255, 255, 255, 255, 255, 254, 254, 255, 255, 255, 255, 255, 255, 255, 254, 255, 255, 255, 255, 254, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255], dtype=uint8)
各次元に `uint8_t` の全範囲 `[0,255]` を使用していることに注意してください（浮動小数点の不正確さのため、最大値のいくつかは 255 ではなく 254 になっています）。
では、これを `ScalarQuantizer` クラスにまとめてみよう：
python
numpy を np としてインポートする。
クラス ScalarQuantizer：
def __init__(self)：
self._dataset = None
def create(self)：
"""入力データセットに基づいてSQパラメータを計算し、格納する。"""
self._dtype = dataset.dtype # 元のdtype
self._starts = np.min(dataset, axis=1)
self._steps = (np.max(dataset, axis=1) - self._starts) / 255
# 内部データセットは `uint8_t` の量子化を使用する。
self._dataset = np.uint8((dataset - self._starts) / self._steps)
def quantize(self, vector)：
"""SQパラメータに基づいて入力ベクトルを量子化する"""
return np.uint8((vector - self._starts) / self._steps)
def restore(self, vector)：
"""SQパラメータを使って元のベクトルを復元する。"""
return (vector * self._steps) + self._starts
プロパティ
def dataset(self)：
if self._dataset：
return self._dataset
raise ValueError("最初にScalarQuantizer.create()を呼び出す")
>>> データセット = np.random.normal(size=(1000, 128))
>>> 量子化器 = ScalarQuantizer(dataset)
スカラー量子化は以上である！スカラー量子化の変換関数は、上の例のように線形関数ではなく、2次関数や指数関数に変更することもできますが、ベクトルデータの全体的なメモリフットプリントを減らすために、各次元の空間全体を離散的なビンに分割するという一般的な考え方は変わりません。
積の量子化
積量子化(PQ)は、スカラー量子化と比較して、ベクトルを量子化するのに非常に強力で柔軟性がある別のデータ圧縮技術です。スカラー量子化の大きな欠点は、各次元における値の分布を考慮しないことです。例えば、次のような2次元ベクトルを持つデータセットがあるとしよう：
array([ [ 9.19, 1.55]、
[ 0.12, 1.55],
[ 0.40, 0.78],
[-0.04, 0.31],
[ 0.81, -2.07],
[ 0.29, 0.82],
[ 0.05, 0.96],
[ 0.12, -1.10]])
これらのベクトルを3ビットの整数（範囲 [0,7]）に量子化することにすると、0次元のビンのうち6ビンはまったく使われないことになる！特に次元の分布が一様でない場合、量子化を行うにはもっと良い方法があるはずです。そこで、積量子化が役に立つのです。
積量子化はどのように機能するのか？
積量子化の主な考え方は、高次元ベクトルを低次元の部分空間にアルゴリズム的に分割することで、部分空間の次元は元の高次元ベクトルの複数の次元に対応します。ロイドアルゴリズムは、k-meansクラスタリングに相当する量子化手法である。スカラー量子化と同様に、各元ベクトルは量子化後の整数ベクトルとなり、各整数は特定の重心に対応する。
これは複雑に聞こえるかもしれないが、アルゴリズムの観点から分解すると、はるかに理解しやすくなる。まずインデックス付けについて説明しよう：
N個のベクトルからなるデータセットが与えられたら、まず各ベクトルをM個の部分ベクトル（subspaceとしても知られている）に分割する。これらの部分ベクトルは必ずしも同じ長さである必要はないが、実際にはほとんどの場合同じ長さになる。- 次に、データセット内のすべての部分ベクトルに対してk-means（または他のクラスタリング・アルゴリズム）を使用する。これによって、それぞれの部分空間に対して
K個のセントロイドのコレクションが得られ、それぞれに固有のIDが割り当てられる。 - すべてのセントロイドが計算されたので、元のデータセットのすべての部分ベクトルを、最も近いセントロイドのIDで置き換える。
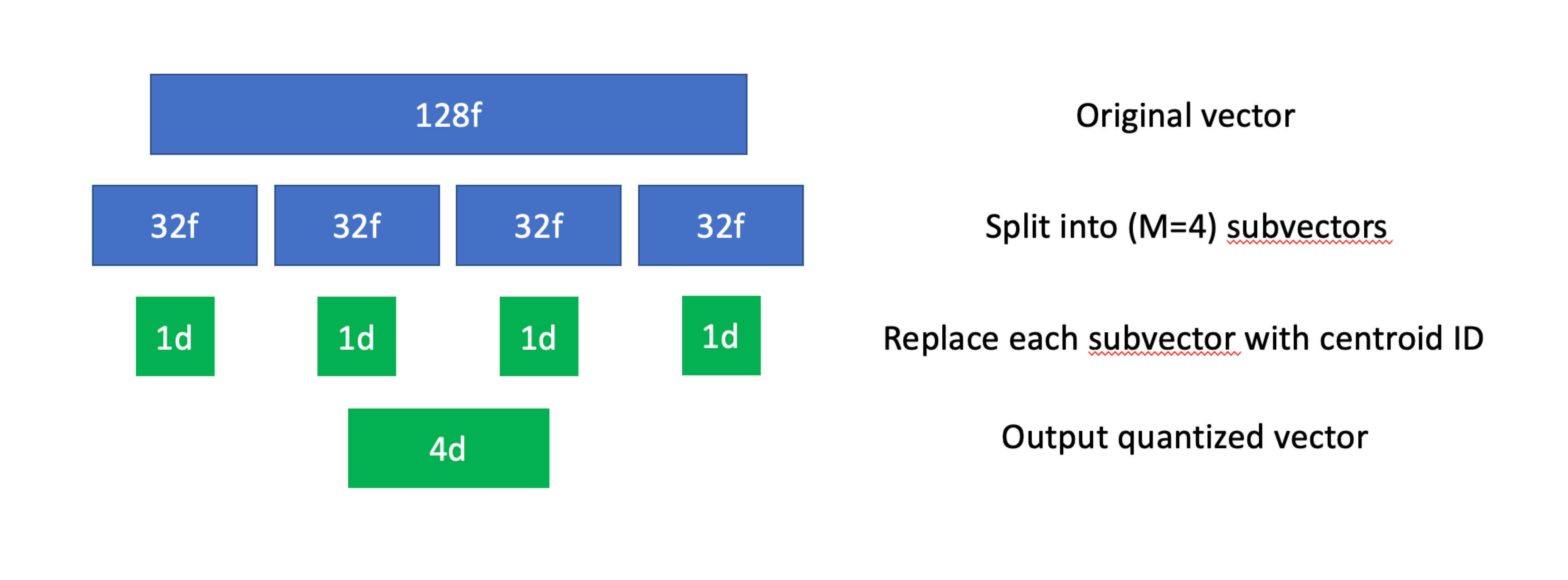積の量子化、可視化。
PQはメモリ使用量を削減し、精度を少し犠牲にすることで最近傍探索の速度を著しく向上させることができます。より多くのセントロイドとサブベクタを使用すると、検索精度は向上しますが、圧縮やスピードアップはあまり期待できません。
非常に単純なPQの実装を見てみよう。先ほどのスカラー量子化の例と同様に、M = 16とK = 256を使ってベクトルを8ビットの符号なし整数（uint8_t`）にします。つまり、各128Dベクトルをサイズ8の16個のサブベクトルに分割し、各サブベクトルを256個のバケットのいずれかに量子化します。
パイソン
(m, k) = (16, 256)
スカラー量子化の例でやったように、おもちゃのデータセットを生成することから始めよう：
python
>>> np として numpy をインポートする。
>> dataset = np.random.normal(size=(1000, 128))
データセットが手に入ったので、最初のサブベクトルのセットを分割してみよう：
``python
sublen = dataset.shape[1] // M subspace = dataset[:,0:sublen] # これは0番目の部分空間である． subspace.shape (1000, 8)
IVFと同様に、scipyの `kmeans2` 実装を用いてセントロイドを決定する：
python
>>> from scipy.cluster.vq import kmeans2
>> (centroids, assignments) = kmeans2(subspace, K, iter=32)
scipyのk-meansの実装はセントロイドのインデックスを int32_t フォーマットで返すので、 uint8_t に変換してまとめる：
python
quantized = np.uint8(assignments)
すべてのベクトルを量子化するまで、この処理を部分空間ごとに繰り返す。
スカラー量子化で行ったように、ここでもすべてをクラスにコンパイルしよう：
python
import numpy as np
from scipy.cluster.vq import kmeans2
class ProductQuantizer：
def __init__(self, M=16, K=256)：
self.M = 16
self.K = 256
self._dataset = None
def create(self, dataset)：
"""入力データセットに基づいてPQモデルをフィットする"""
sublen = dataset.shape[1] // self.M
self._centroids = np.empty((self.M, self.K, sublen), dtype=np.float64)
self._dataset = np.empty((dataset.shape[0], self.M), dtype=np.uint8)
for m in range(self.M)：
subspace = dataset[:,m*sublen:(m+1)*sublen].
(centroids, assignments) = kmeans2(subspace, self.K, iter=32)
self._centroids[m,:,:] = centroids
self._dataset[:,m] = np.uint8(assignments)
def quantize(self, vector)：
"""PQパラメータに基づいて入力ベクトルを量子化する"""
量子化 = np.empty((self.M,), dtype=np.uint8)
for m in range(self.M)：
セントロイド = self._centroids[m,:,:].
distances = np.linalg.norm(vector - centroids, axis=1)
量子化[m] = np.argmin(distances)
quantizedを返す
def restore(self, vector)：
"""PQパラメータを使って元のベクトルを復元する。"""
return np.hstack([self._centroids[m,vector[m],:] for m in range(M)])
プロパティ
def dataset(self)：
if self._dataset：
return self._dataset
raise ValueError("最初にProductQuantizer.create()を呼び出す")
>> dataset = np.random.normal(size=(1000, 128))
>> quantizer = ProductQuantizer()
>> quantizer.create(dataset)
これで積の量子化は完了だ！探索処理を高速化するために、各サブスペースのすべてのセントロイドのdistance tablesを計算するために少しメモリを消費することができますが、それは練習として残しておきます。
まとめ
このチュートリアルでは、スカラー量子化と積量子化について深く掘り下げ、簡単な実装を作成しました。スカラー量子化は良いツールですが、積量子化はより強力で、ベクトルデータの分布に関係なく使うことができます。PQはメモリフットプリントを減らしながらクエリー時間を大幅にスピードアップするのに役立ちますが、一般的にリコールにはあまり向いていないことを覚えておいてください。今後のチュートリアルで、PQと他のインデックス戦略をベンチマークします。
次回のチュートリアルでは、HNSW（Hierarchical Navigable Small Worlds：階層的ナビゲーシブルスモールワールド）を用いて、インデックス戦略を深く掘り下げていきます。次回のチュートリアルでお会いしましょう！
このチュートリアルのコードはすべてGithubで自由に利用できます: https://github.com/fzliu/vector-search.
ベクターデータベース101コースをもう一度見てみよう
1.非構造化データ入門 2.ベクターデータベースとは 3.ベクトルデータベース、ベクトル検索ライブラリ、ベクトル検索プラグインの比較 4.Milvusの紹介 5.Milvusクイックスタート 6.ベクトル類似検索入門 7.ベクトルインデックスの基本と反転ファイルインデックス 8.スカラー量子化と積量子化 9.階層的航行可能小世界(HNSW) 10.近似最近傍オーイェー(ANNOY) 11.プロジェクトに適したベクトルインデックスの選択 12.DiskANNとVamanaアルゴリズム
読み続けて
AI Integration in Video Surveillance Tools: Transforming the Industry with Vector Databases
Discover how AI and vector databases are revolutionizing video surveillance with real-time analysis, faster threat detection, and intelligent search capabilities for enhanced security.
Building Secure RAG Workflows with Chunk-Level Data Partitioning
Rob Quiros shared how integrating permissions and authorization into partitions can secure data at the chunk level, addressing privacy concerns.
Building RAG Applications with Milvus, Qwen, and vLLM
In this blog, we will explore Qwen and vLLM and how combining both with the Milvus vector database can be used to build a robust RAG system.