ベクトル探索のための類似度メトリクス
検索のための#ベクトル類似度メトリクス - Zilliz Blog
リンゴとオレンジを比べることはできない。そうだろうか？Milvus](https://zilliz.com/what-is-milvus)のようなベクターデータベースを使えば、あらゆるベクター化できるデータを比較することができる。Jupyter Notebook](https://zilliz.com/blog/exploring-magic-vector-databases-jupyter-notebooks)の中でだってできる。しかし、ベクトル類似性検索はどのように機能するのでしょうか？
ベクトル検索には、インデックスと距離メトリクスという2つの重要な概念的要素がある。よく使われるベクトル・インデックスには、HNSW、IVF、ScaNNなどがあります。3つの主要な距離メトリックがある：L2またはユークリッド距離、余弦類似度、内積である。マンハッタン距離は、各次元間の差の絶対値を合計することで点間の距離を計算し、外れ値の感度を最小化する必要があるシナリオで有利である。バイナリ・ベクトルに対する他のメトリックスには、ハミング距離とジャカード指数があります。
この記事では
ベクトル類似度メトリクス
L2またはユークリッド
L2 距離はどのように機能するのか？
どのような場合にユークリッド距離を使うべきか？
コサイン類似度
コサイン類似度はどのように機能するか？
コサイン類似度はいつ使うべきか？
内積
内積はどのように機能するか？
いつインナープロダクトを使用する必要がありますか？
その他の興味深いベクトル類似度または距離メトリクス
ハミング距離
ジャカード指数
ベクトル類似度検索指標の概要
ベクトルは数値のリストとして、または方向と大きさで表すことができます。これを理解する最も簡単な方法は、ベクトルを空間の特定の方向を指す線分として想像することです。
L2またはユークリッド計量は、2つのベクトルの「斜辺」計量です。L2またはユークリッド測度は、2つのベクトルの "斜辺 "測度です。これは、ベクトルの線の終点間の距離の大きさを測ります。
余弦類似度**は、2つの直線が交わる角度のことです。
内積**は、一方のベクトルを他方のベクトルに「投影」したものです。直感的には、ベクトル間の距離と角度の両方を測定します。
最も直感的な距離尺度はL2またはユークリッド距離です。これは、2つのオブジェクト間の空間の大きさと想像することができる。例えば、スクリーンとあなたの顔の距離だ。
L2距離が空間でどのように機能するかは想像できたが、数学ではどのように機能するのだろうか？まず、両方のベクトルを数字のリストとして想像してみよう。両者のリストを重ねて並べ、下に向かって引き算をする。次に、すべての結果を二乗して足し算する。最後に平方根をとる。
Milvusは平方根と非平方根の順位が同じなので平方根をスキップする。このように、演算をスキップしても同じ結果が得られるので、レイテンシとコストが下がり、スループットが向上する。以下は、ユークリッド距離またはL2距離がどのように機能するかの例である。
d(Queen, King) = √(0.3-0.5)2 + (0.9-0.7)2
= √(0.2)2 + (0.2)2
= √0.04 + 0.04
= √0.08 ≅ 0.28
ユークリッド[距離]を使う主な理由の一つは、ベクトル](https://zilliz.com/glossary/vector-distance)の大きさが異なる場合です。ユークリッド[距離]を使う主な理由のひとつは、ベクトルの大きさが異なる場合です]()。
私たちは、2つのベクトルの向きの違いを表すために、「余弦類似度」や「余弦距離」という言葉を使います。例えば、玄関のドアに向かうために、あなたはどこまで向きを変えるだろうか？
楽しくて応用可能な事実：「類似性」と「距離」は単独では異なる意味を持っているにもかかわらず、両方の用語の前にコサインを加えると、ほとんど同じ意味になる！これは、意味類似性のもう一つの例である。
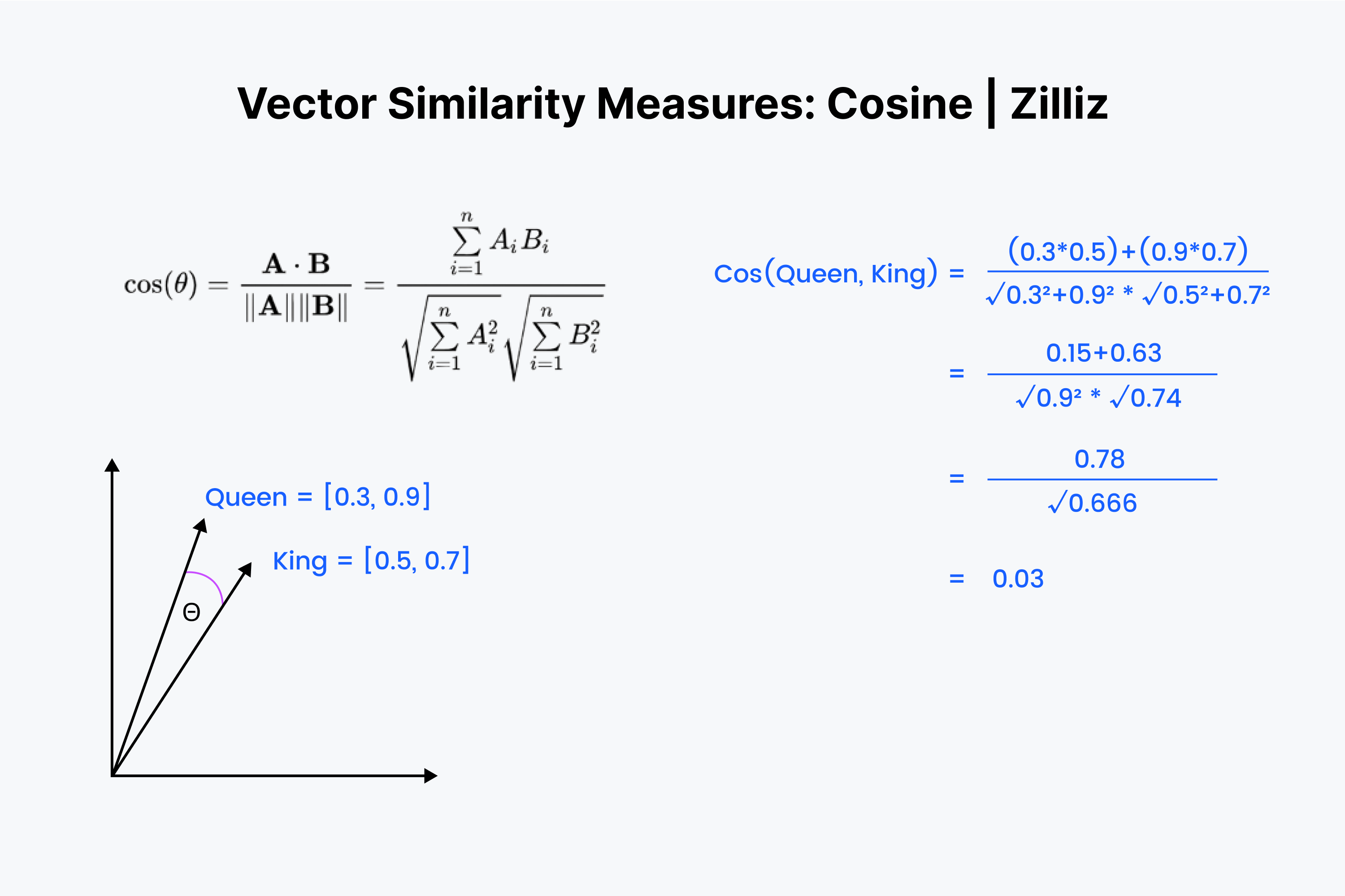
つまり、余弦類似度は2つのベクトル間の角度を測定することがわかります。もう一度、ベクトルを数値のリストとして想像してみよう。しかし、今回は少し複雑だ。
まず、ベクトル同士を重ねることから始める。まず数字を掛け算し、その結果をすべて足し算する。その数字を "x "と呼んで保存する。次に、各数値を2乗し、各ベクトルの数値を足す。それぞれの数字を水平に2乗し、両方のベクトルについて足し算することを想像してください。
両方の和の平方根をとり、それらを掛け合わせ、この結果を "y "と呼ぶ。x "を "y "で割ったものが余弦距離となる。
コサイン類似度は主にNLPアプリケーションで使われる。コサイン類似度が測定する主なものは、意味方向の違いである。正規化されたベクトルを扱う場合、コサイン類似度は内積と等価である。
内積は一方のベクトルを他方のベクトルに射影したものである。内積の値はベクトルの長さを引いたものである。2つのベクトル間の角度が大きいほど、内積は小さくなる。また、内積は小さい方のベクトルの長さに比例する。だから、向きや距離を気にするときには内積を使う。例えば、冷蔵庫まで壁を通って直線距離を走らなければならない。
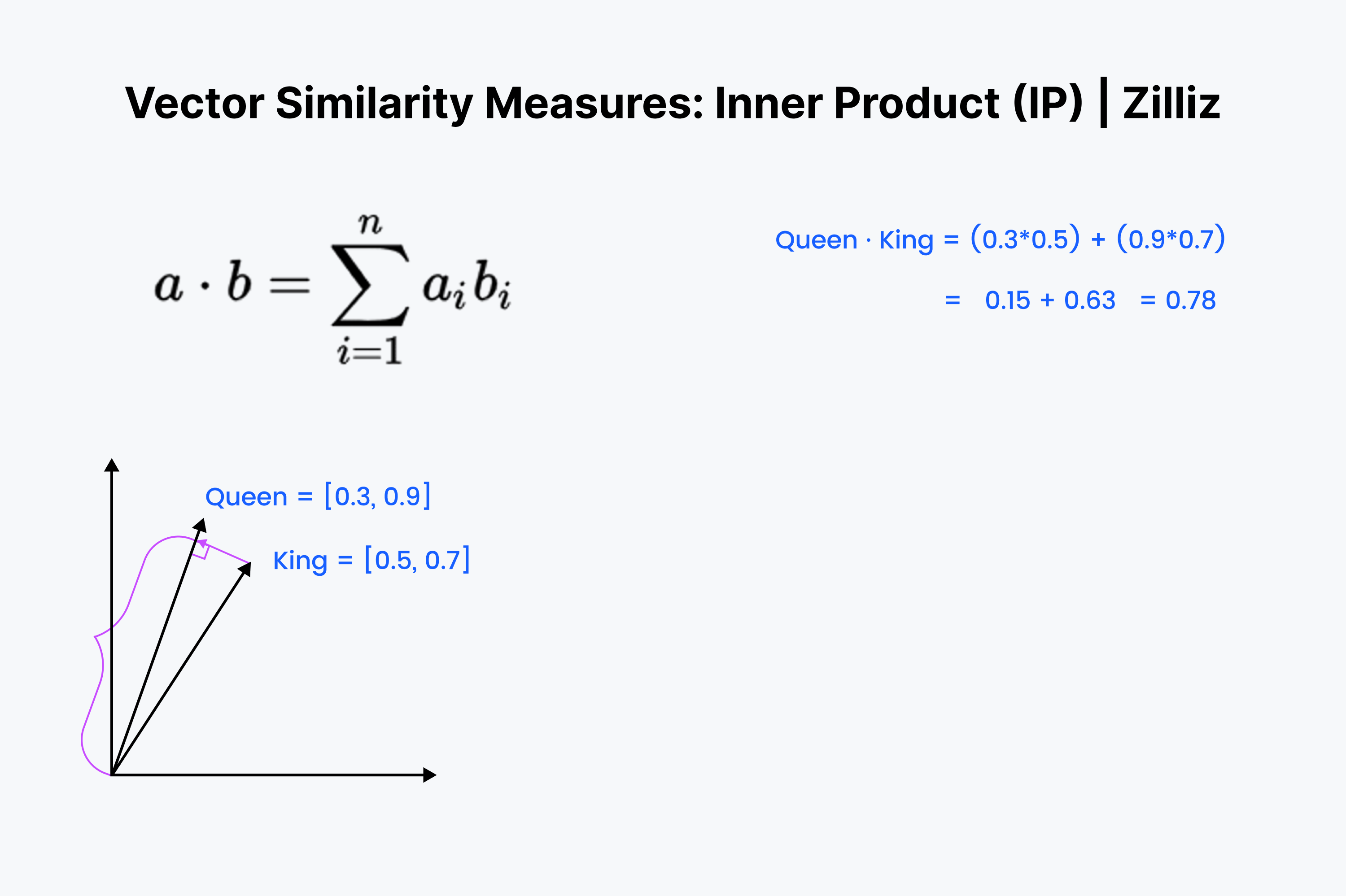
内積は見慣れたものだろう。これは余弦計算の最初の⅓に過ぎない。これらのベクトルを頭の中で並べ、行を下へ下へと掛け合わせる。そしてそれらを合計する。これは、あなたと最も近いディムサムとの間の直線距離を測定する。
内積はユークリッド距離と余弦類似度を掛け合わせたようなものだ。正規化されたデータセットに関しては、コサイン類似度と同じなので、IPは正規化されたデータセットにも正規化されていないデータセットにも適している。コサイン類似度よりも高速で、より柔軟なオプションである。
内積の注意点は、三角形の不等式に従わないことです。より大きな長さ（大きな大きさ）が優先されます。つまり、IPをInverted File IndexやHNSWのようなグラフ・インデックスと併用する場合は注意が必要です。
ベクトル埋め込み](https://zilliz.com/glossary/vector-embeddings)に関しては、上記の3つのベクトル・メトリクスが最も有用です。しかし、2つのベクトル間の距離を測る方法はこれだけではありません。ここでは、ベクトル間の距離や類似度を測定する他の2つの方法を紹介します。
グループ 13401.png](https://assets.zilliz.com/Group_13401_dc84119c7f.png)
ハミング距離はベクトルにも文字列にも適用できます。今回の使用例では、ベクトルに限って説明しよう。ハミング距離は、2つのベクトルの*エントリーの「差」を測定します。例えば、"1011 "と "0111 "のハミング距離は2である。
ベクトル埋め込みにおいて、ハミング距離が意味を持つのは2値ベクトルの場合だけです。ニューラルネットワークの最後から2番目の層の出力であるFloat vector embeddingsは、0～1の浮動小数点数で構成される。例えば、[˶[0.24, 0.111, 0.21, 0.51235]や[˶[0.33, 0.664, 0.125152, 0.1]などがある。
ご覧のように、2つのベクトル埋め込み間のハミング距離は、ほとんどの場合、ベクトル自体の長さだけになります。それぞれの値の可能性が多すぎるのです。そのため、ハミング距離は2値または疎なベクトルにしか適用できないのです。TF-IDF](https://zilliz.com/learn/tf-idf-understanding-term-frequency-inverse-document-frequency-in-nlp)、BM25、SPLADEのような処理から生成されるベクトルのタイプです。
ハミング距離は、2つのテキスト間の言葉遣いの違い、単語のスペルの違い、2つのバイナリ・ベクトルの違いなどを測定するのに適しています。しかし、ベクトル埋め込み間の差の測定には向いていません。
面白い事実があります。ハミング距離は、2つのベクトルに対するXOR演算の結果の和と等価です。
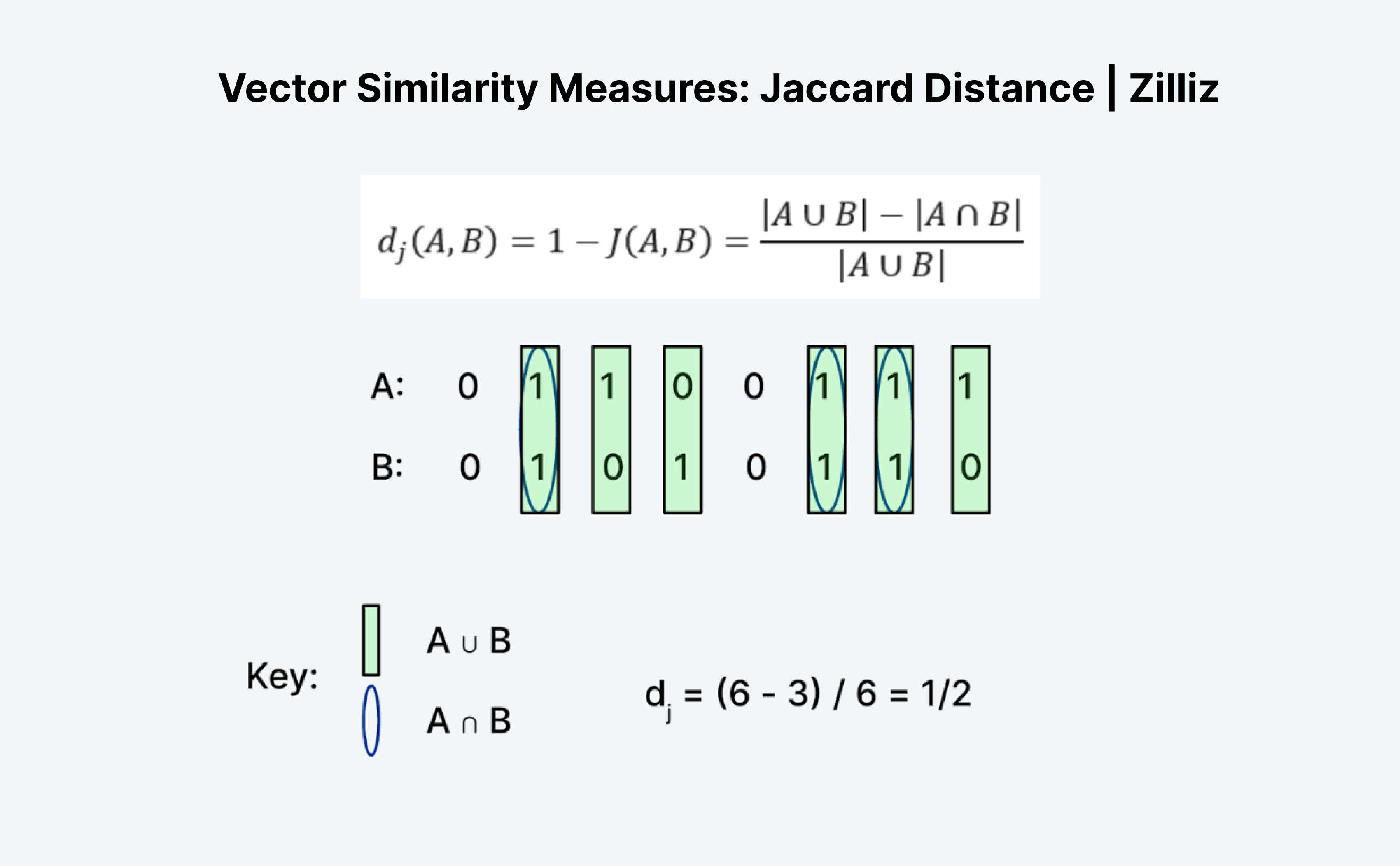
Jaccard距離は2つのベクトルの類似性や距離を測るもう1つの方法です。Jaccardの面白いところは、Jaccard IndexとJaccard Distanceの両方があることです。Jaccard距離は1からJaccardインデックスを引いたもので、Milvusが実装している距離メトリックです。
Jaccard距離やインデックスを計算するのは、一見すると正確には意味をなさないので、興味深い作業である。ハミング距離のように、ジャカードはバイナリデータにしか使えない。ユニオン」と「インターセクション」という伝統的な成り立ちが混乱させるのだ。私が考える方法は論理です。基本的には、A "OR "BからA "AND "Bを引いたものをA "OR "Bで割ったものだ。
上の図のように、AかBのどちらかが1であるエントリーの数を "ユニオン"、AとBの両方が1であるエントリーの数を "インターセクション "と数える。つまり、A(01100111)とB(01010110)のジャカード指数は1/2である。この場合、1からジャカード指数を引いたジャカード距離も1/2となる。
この投稿では、最も有用な3つのベクトル類似検索メトリクスについて学びました：L2（ユークリッド）距離、余弦距離、内積です。それぞれ、使用するケースが異なります。ユークリッド距離は、大きさの違いに注目する場合に使用します。コサインは方位の違いを気にするときに使う。内積は、大きさと向きの違いを気にするときに使う。
ベクトル類似度メトリクスの詳細についてはビデオを、Milvusでの設定方法についてはドキュメントを読むをご覧ください。
類似度メトリクス入門
類似度メトリクスは様々なデータ分析や機械学習タスクにおいて重要なツールです。これにより、異なるデータ間の類似性を比較・評価することができ、クラスタリング、分類、レコメンデーションなどの応用が容易になります。数多くの類似性メトリクスがあり、それぞれに長所と短所があるため、特定のタスクに適したものを選択することは困難です。このセクションでは、類似性メトリクスの概念とその重要性を紹介し、最も一般的に使用されているメトリクスの概要を示します。
コサイン類似度
コサイン類似度は、2つのベクトル間の角度の余弦を測定する、広く使用されている類似度メトリックです。自然言語処理や情報検索のタスクでよく使われます。コサイン類似度メトリックは、計算効率が高く、疎なデータを扱うことができるため、高次元データを扱う場合に特に有用である。2つのベクトル間の余弦類似度は、ベクトルのドット積をそれらの大きさの積で割ることで計算できる。
ユークリッド距離
ユークリッド距離は，直線距離としても知られ，n次元空間の2点間の距離を測定する，広く使われている距離尺度である．これは2つのベクトルの対応する要素間の差の2乗の和の平方根として計算される。ユークリッド距離は、クラスタリング、分類、回帰分析など様々なアプリケーションで一般的に使用されている。しかし、外れ値の影響を受けやすく、高次元データではうまく機能しないことがある。
正しい類似度メトリックの選択
適切な類似度メトリックの選択は、データの種類、分析目的、変数間の関係などの様々な要因に依存する。例えば、コサイン類似度は高次元データや自然言語処理タスクに適しており、ユークリッド距離はクラスタリングや分類タスクによく使われる。L1距離としても知られるマンハッタン距離は外れ値のあるデータに適しており、ハミング距離はバイナリデータに使用される。特定のタスクに最も適したものを選択するためには、各類似度メトリックの特性と限界を理解することが不可欠である。
実際のアプリケーション
類似度メトリクスは、以下のような様々な分野で実世界に数多く応用されています：
自然言語処理：コサイン類似度は、テキスト分類、感情分析、情報検索タスクに広く使用されている。
推薦システム：コサイン類似度やユークリッド距離のような類似度メトリクスは、ユーザの行動や嗜好に基づいて製品やサービスを推薦するために使用される。
画像・映像解析：ユークリッド距離やマンハッタン距離などの類似度メトリッ クは、画像や動画の分類、物体検出、追跡タスクに使用される。
クラスタリングと分類：クラスタリングと分類：ユークリッド距離やコサイン類似度などの類似度メトリクスは、クラスタリングと分類タスクで使用され、類似のデータポイントをグループ化します。
結論として、類似性メトリクスは様々なデータ分析や機械学習タスクにおいて重要なツールです。各類似度メトリックの特徴と限界を理解することは、特定のタスクに最も適切なものを選択するために不可欠である。適切な類似性メトリックを選択することで、結果の精度と関連性を向上させ、より良い意思決定と洞察につなげることができる。
Yujian TangYujian Tang is a Developer Advocate at Zilliz. He has a background as a software engineer working on AutoML at Amazon. Yujian studied Computer Science, Statistics, and Neuroscience with research papers published to conferences including IEEE Big Data. He enjoys drinking bubble tea, spending time with family, and being near water.
読み続けて
Beyond PGVector: When Your Vector Database Needs a Formula 1 Upgrade
This blog explores why Postgres, with its vector search add-on, pgvector, works well for smaller projects and simpler use cases but reaches its limits for large-scale vector search.
Semantic Search vs. Lexical Search vs. Full-text Search
Lexical search offers exact term matching; full-text search allows for fuzzy matching; semantic search understands context and intent.
Designing Multi-Tenancy RAG with Milvus: Best Practices for Scalable Enterprise Knowledge Bases
We’ve explored how multi-tenancy frameworks play a critical role in the scalability, security, and performance of RAG-powered knowledge bases.