Understanding the CURE Algorithm: A Comprehensive Exploration of Clustering with Representatives

Glossary
CURE Algorithm

Understanding the CURE Algorithm: A Comprehensive Exploration of Clustering with Representatives

Visual Representation of Clustering

Figure 1: Visual Representation of Clustering

How can businesses navigate the ever-changing marketplace and effectively group customers with similar patterns? Traditional clustering methods often fall short when dealing with irregular data shapes and outliers. The complexity of modern datasets demands smarter, more adaptable solutions.

Enter the CURE (Clustering Using Representatives) algorithm, an effective method that addresses the constraints of standard clustering approaches. CURE uses a selection of representative points to differentiate itself from classic clustering methods, thus improving its intelligence in discerning complex data distributions. These representative points move closer to the mean of the cluster, making the algorithm more advanced by allowing it to deal with arbitrary-shaped clusters.

CURE can become computationally intensive when applied to large datasets. Despite this, its approach to handling anomalies and complex clusters remains highly effective. Let’s discuss the CURE algorithm operations by exploring its core approach, advantages, and practical applications. We will also go over the challenges you may face while implementing CURE.

What Is the CURE Algorithm?

The CURE algorithm uses a hierarchical clustering approach, which identifies intricate cluster shapes and effectively handles outliers. ****Unlike centroid-based algorithms such as k-means, CURE represents clusters using multiple representative points. These points move toward cluster means with a fixed shrink factor to create resilient cluster representations.

CURE demonstrates better flexibility than k-means because its design allows it to work with various irregular dataset types. Its ability to overcome traditional algorithm constraints regarding convex or equidistant clusters leads to the precise detection of cluster boundaries and shapes.

How It Works

CURE algorithms involve multiple steps to produce the final output. Let's uncover how they select data to create a cluster free of outliers.

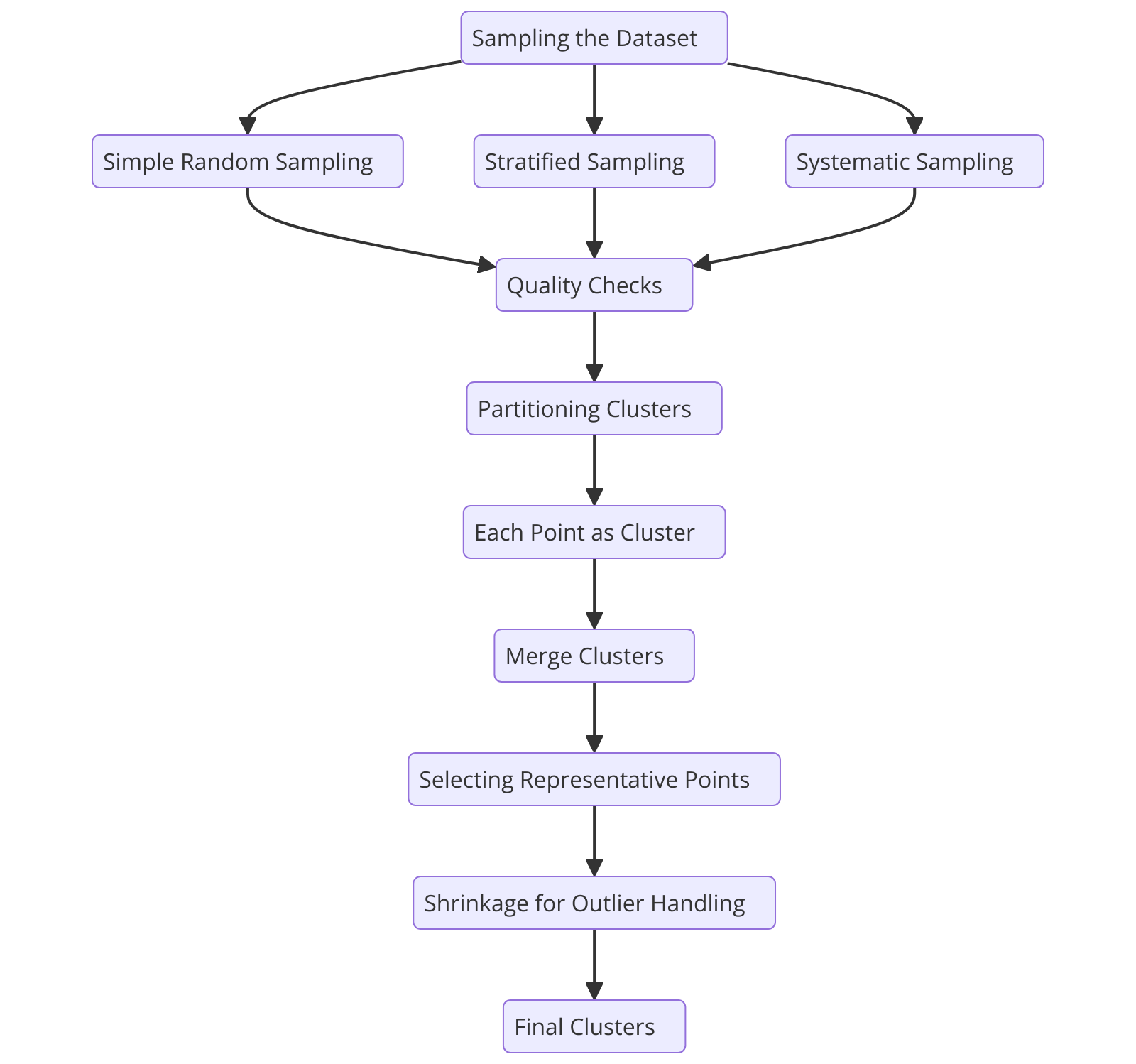CURE Clustering Algorithm Process Flow

Figure 2: CURE Clustering Algorithm Process Flow

CURE Clustering Algorithm Process Flow

To understand how the CURE algorithm works, let's break down its process step by step, starting with sampling the dataset.

Sampling the Dataset

CURE starts by selecting a representative random sample from the dataset. The sampling process decreases the number of data points, accelerating computation speed while maintaining cluster integrity.

Simple random sampling provides quick implementation but fails to capture crucial edge cases. This produces inadequate representation of minority groups in unbalanced datasets. Stratified sampling becomes necessary when the proportionate distribution of different classes in the data needs to be maintained.

This method ensures that all significant small subsets of data remain visible for analysis. Another method is systematic sampling, which picks data points through a regular interval system. Systematic sampling excels in time series and ordered data since it preserves the temporal nature and sequential ordering pattern in datasets.

Quality checks verify the sample's consistency with the original dataset distribution after collection. Comparing mean values, variance levels, and distribution characteristics helps assess the similarities between the obtained sample and the complete original dataset. Rigorous sampling strategies implemented by CURE enable subsequent clustering to accurately represent the complexity and diversity of the entire dataset.

Partitioning Clusters

After sampling the dataset, CURE applies a hierarchical method that divides the data into manageable subsets. Notably, it uses a bottom-up merging strategy for clustering. The algorithm measures data point similarities through distance metrics that use Euclidean distance or Manhattan distance. The distance calculation metrics are essential for determining point proximity while establishing a solid basis for effective cluster merging.

At the beginning of the process, each data point functions as its cluster to represent the fine-grained nature of the data. The algorithm performs successive cluster merges using proximity standards to group similar points. The algorithm continues through cluster merging operations until a defined number of clusters is reached or an alternative termination condition activates.

The group selection process in CURE creates clusters that align with the natural categories present in the data. By using hierarchical partitioning, CURE overcomes the limitations of traditional clustering algorithms that require clusters to have convex shapes.

Selecting Representative Points

CURE selects multiple representative points to represent each cluster rather than depending on a single centroid. These points, carefully chosen from the cluster, capture its spatial range and structure. CURE achieves better cluster boundary recognition and internal structure comprehension by using multiple points to represent each cluster.

After selecting representative points, the algorithm moves them toward the cluster mean with a specified shrinkage amount. The shrinkage procedure makes the algorithm less reactive to outliers by moving distant points toward cluster central points.

The algorithm's success depends heavily on how many representative points are used during execution. The appropriate selection of representative points is crucial. Using few representative points may fail to capture the cluster complexity, while using too many can increase computational costs.

Merging Clusters

After identifying the representative points, the algorithm merges clusters using a systematic iterative approach. The procedure depends on measuring the distance between representative points of different clusters. Predefined metrics, such as Euclidean distance, are used to measure distances, thus eliminating conflicts in finding the nearest clusters.

The algorithm identifies which cluster pairs have the least distance from the representative point separation during every evaluation step. The algorithm makes accurate cluster merging decisions while preserving spatial relationships and natural data alignment patterns inside clusters.

The process iterates until some predetermined clusters are achieved or another termination criterion is achieved. The termination criterion depends on factors such as the minimum distance between clusters or the maximum allowable similarity within clusters. This assures that the produced clusters correspond to the natural groupings in the data and are flexible enough to capture irregular and complex shapes.

Outlier Handling

When outliers exist, the results become distorted because they cause incorrect cluster shapes and misinterpret the data structure. The CURE algorithm solves these limitations using multiple representative points, which accurately identify clusters' actual shape and distribution.

The shrinking mechanism represents another fundamental advancement in CURE, making the system more resilient and increasing its sophistication. This deliberate adjustment decreases the algorithm's sensitivity to extreme values, moving representative points toward cluster center positions.

The shrink factor is a tuning parameter that allows users to customize its value according to dataset characteristics. This enables flexible outlier mitigation while preserving cluster natural boundaries.

Comparison with Other Clustering Methods

The CURE algorithm’s innovative approach distinguishes it from other popular clustering techniques. Here’s a deeper comparison:


Aspect	CURE	k-means	DBSCAN
Representation	Multiple representative points	Single centroid	Density-based
Outlier Handling	Excellent	Poor	Good
Shape Flexibility	Arbitrary shapes	Convex shapes only	Arbitrary shapes
Scalability	High (with sampling)	High	Moderate
Complexity	Higher	Lower	Moderate

Benefits and Challenges

When applied to real-world scenarios, CURE offers a mix of advantages and challenges. Let’s discuss how CURE can offer value while also presenting certain hurdles in practical applications.

Benefits

Scalability: CURE achieves scalability through its data sampling strategy, which reduces computational workloads without compromising cluster precision accuracy.
Robustness: CURE increases robustness by using multiple representative point to capture the form and structure of a cluster. Thus, clustering will yield reliable and stable results even when the data is noisy and inconsistent.
Versatility: CURE captures clusters of any shape and handles irregularities or non-convex structures. This is particularly useful in diverse datasets, where traditional techniques such as k-means fail to represent them accurately.

Challenges

Parameter Sensitivity: The algorithm requires precise parameter adjustment for the shrink factor and the number of representative points. Finding the right balance is crucial for optimal performance, requiring both experimentation and domain expertise.
Sampling Bias: Insufficient sampling techniques produce inaccurate cluster formation and poor outcomes. Maintaining unbiased representative samples is essential to ensuring that dataset structures remain intact.
Computational Demands: CURE's scalability challenges increase with large, high-dimensional, or unstructured datasets due to the need for multiple distance evaluations. Techniques like PCA and parallel computing can reduce dimensionality, lowering computational costs while preserving key relationships.

Use Cases

To see the CURE algorithm's practical impact, let’s go over how it can solve real-world clustering challenges across various domains.

Anomaly detection

CURE effectively identifies anomalies by grouping typical transactions and isolating irregular ones that may indicate fraud. This enables financial institutions to detect suspicious activities quickly and enhance their security measures.

Market segmentation

In marketing, CURE can segment customers based on attributes such as purchasing behavior, demographics, and preferences. This enable targeted marketing campaigns, improving customer retention, and predicting future trends. For example, high-value customers can be clustered for exclusive offers to increase loyalty.

Geospatial data analysis

Urban planners can implement CURE to categorize regions with similar climates, population densities, or infrastructure developments. Environmental scientists can use it to cluster areas according to their biodiversity and resource availability while studying ecosystems.

Document clustering

CURE demonstrates excellent effectiveness in text mining by grouping extensive document catalogs based on their standard themes and topics. Search engines use this method to create precise result categories that enable users to find relevant content quickly.

CURE enables recommendation systems to identify articles and research papers with similar subjects. This results in personalized, meaningful recommendations for users. CURE can effectively cluster diverse text structures to maintain precise grouping results regardless of the complexity and size of high-dimensional datasets. The algorithm adapts well to multilingual text datasets and heterogeneous data entries, positioning it as an essential solution for contemporary information retrieval platforms.

Conclusion

The CURE clustering algorithm stands as a major breakthrough in clustering methods. It delivers an effective and scalable solution for contemporary data problems. The algorithm uses representative points alongside hierarchical principles to overcome traditional clustering limitations while ensuring flexible and accurate results. While the algorithm faces challenges with parameter optimization and computational requirements, its ability to manage noisy data and complex patterns is essential for multiple business sectors.

The growing complexity of datasets will continue to boost the need for flexible clustering algorithms like CURE in the future. Data scientists and machine learning practitioners who understand CURE principles will be able to maximize their potential for generating meaningful insights from complex datasets.

FAQs

What makes CURE unique compared to k-means?

CURE distinguishes itself from k-means by utilizing multiple representative points instead of a single cluster centroid. The method enables the detection of irregular cluster shapes and non-linear patterns across complex datasets without requiring convex cluster assumptions.

How does CURE handle large datasets?

CURE manages large datasets through random sampling techniques that minimize computational processing requirements. The sampling strategy enables the algorithm to process reduced data subsets, preserving the integrity of cluster relationships.

What is the role of the shrink factor in CURE?

The CURE shrink factor controls the distance at which representative points move toward their cluster's mean position. This factor enables users to achieve optimal results between accuracy and robustness. The success of CURE implementations depends heavily on discovering the correct shrink factor for each dataset.

Can CURE work with high-dimensional data?

Using CURE algorithms on high-dimensional data requires prior preprocessing through techniques such as PCA. High-dimensional data processing requires efficient dimension reduction to find essential patterns even when maintaining data simplicity.

What are the typical applications of CURE?

CURE's typical applications include anomaly detection, market segmentation, geospatial analysis, and document clustering analysis. It can identify unusual financial patterns for fraud detection, group customers by behavior, and analyze regions based on characteristics.

Content

Start Free, Scale Easily

Try the fully-managed vector database built for your GenAI applications.

Try Zilliz Cloud for Free

Share this article

Related Resources

What is a Vector Database?

A vector database is a fully managed, no-frills solution for storing, indexing and searching across a massive dataset of unstructured data that leverages the power of embeddings from machine learning models.

Milvus Performance Evaluation 2023

This is tutorial you will learn about text-based unstructured data.

Introduction to Vector Similarity Search

How semantically similar pieces of unstructured data are “near” and “far” from one another.