Метрики сходства для векторного поиска
Метрики векторного сходства для поиска - Блог Zilliz
Нельзя сравнивать яблоки и апельсины. А вы можете? Векторные базы данных, такие как Milvus, позволяют сравнивать любые данные, которые вы можете векторизовать. Вы даже можете сделать это прямо в своем Jupyter Notebook. Но как работает поиск векторного сходства?
Векторный поиск имеет два важнейших концептуальных компонента: индексы и метрики расстояния. Некоторые популярные векторные индексы включают HNSW, IVF и ScaNN. Существует три основных метрики расстояния: L2 или евклидово расстояние, косинусное сходство и внутреннее произведение. Манхэттенское расстояние рассчитывает расстояние между точками путем суммирования абсолютных разностей по каждому измерению и является преимуществом в сценариях, где необходимо минимизировать чувствительность к выбросам. Другие метрики для бинарных векторов включают расстояние Хэмминга и индекс Жаккара.
В этой статье мы рассмотрим:
Метрики сходства векторов
L2 или евклидово
Как работает расстояние L2?
Когда следует использовать евклидово расстояние?
Косинусное сходство
Как работает косинусное сходство?
Когда следует использовать косинусное сходство?
Внутреннее произведение
Как работает внутреннее произведение?
Когда следует использовать Inner Product?
Другие интересные метрики векторного сходства или расстояния
Расстояние Хэмминга
Индекс Жаккара
Сводка метрик поиска векторного сходства
Векторы могут быть представлены в виде списков чисел или в виде ориентации и величины. Чтобы проще понять это, можно представить векторы как отрезки прямых, направленные в определенные стороны в пространстве.
Метрика L2 или евклидова метрика** - это метрика "гипотенузы" двух векторов. Она измеряет величину расстояния между точками, на которых заканчиваются линии векторов.
Косинусное подобие - это угол между вашими прямыми в месте их пересечения.
Внутреннее произведение - это "проекция" одного вектора на другой. Интуитивно оно измеряет как расстояние, так и угол между векторами.
Наиболее интуитивно понятной метрикой расстояния является L2 или евклидово расстояние. Мы можем представить его как объем пространства между двумя объектами. Например, как далеко ваш экран находится от вашего лица.
Итак, мы представили, как расстояние L2 работает в пространстве, а как оно работает в математике? Для начала давайте представим оба вектора в виде списка чисел. Выстройте списки друг на друге и вычтите их в сторону уменьшения. Затем возведите все результаты в квадрат и сложите их. И наконец, извлеките квадратный корень.
Milvus пропускает квадратный корень, потому что порядок рангов с квадратным корнем и без квадратного корня одинаков. Таким образом, мы можем пропустить операцию и получить тот же результат, уменьшив время ожидания и стоимость и увеличив пропускную способность. Ниже приведен пример того, как работает евклидово или L2-расстояние.
d(Queen, King) = √(0,3-0,5)2 + (0,9-0,7)2
= √(0.2)2 + (0.2)2
= √0.04 + 0.04
= √0.08 ≅ 0.28
Одна из главных причин использовать евклидово расстояние - это когда ваши векторы имеют разные величины. Вас в первую очередь интересует, насколько далеко друг от друга находятся слова в пространстве, или семантическое расстояние.
Мы используем термин "косинусное сходство" или "косинусное расстояние" для обозначения разницы между ориентацией двух векторов. Например, как далеко вы повернетесь, чтобы встать лицом к входной двери?
Забавный и применимый факт: несмотря на то, что "сходство" и "расстояние" имеют разные значения сами по себе, добавление косинуса перед обоими терминами заставляет их означать почти одно и то же! Это еще один пример семантического сходства в игре.
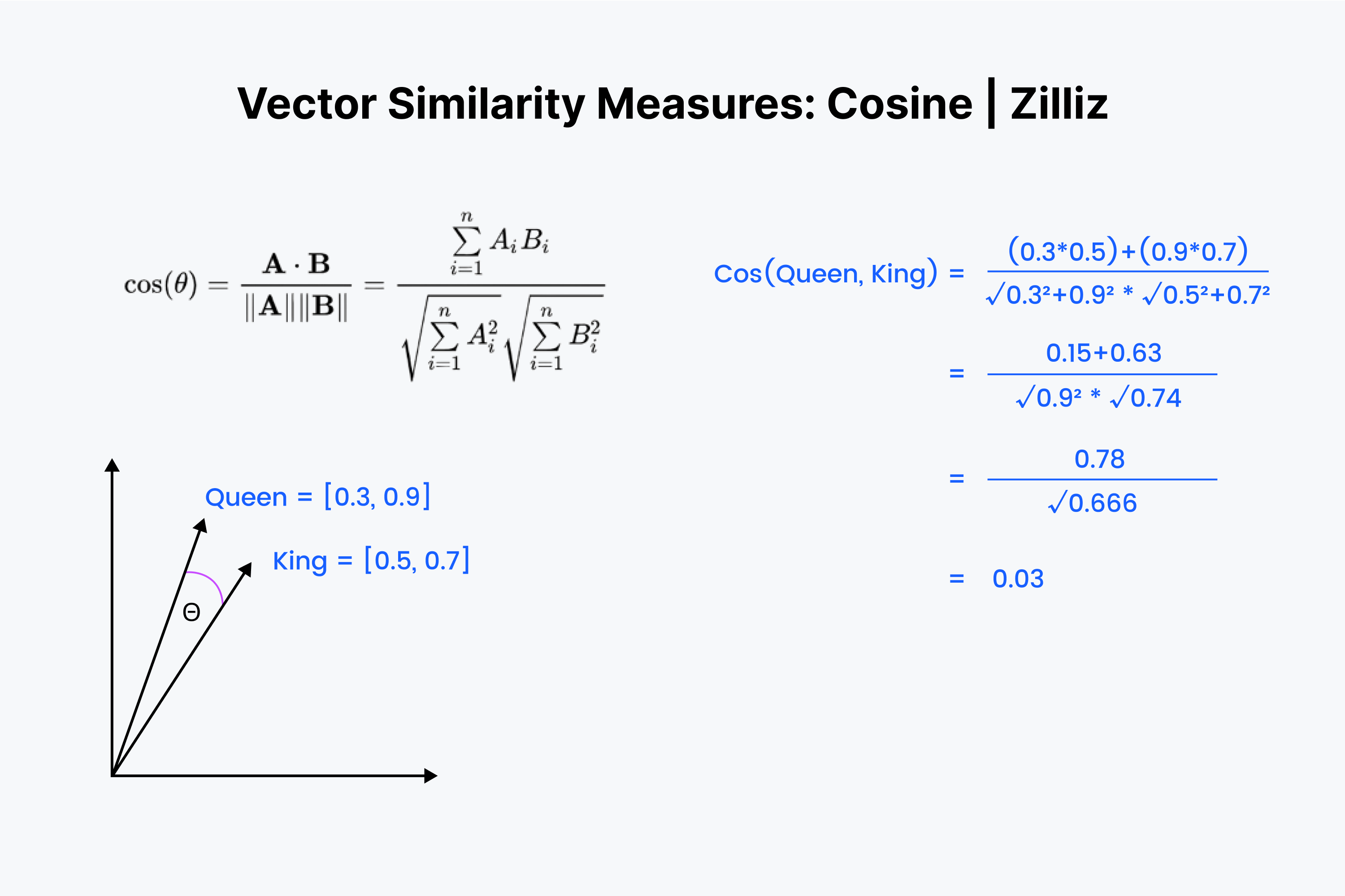
Итак, мы знаем, что косинусное сходство измеряет угол между двумя векторами. И снова мы представляем наши векторы в виде списка чисел. Однако на этот раз процесс немного сложнее.
Начнем с того, что снова наложим векторы друг на друга. Начните с умножения чисел вниз, а затем сложите все результаты. Теперь сохраните это число; назовите его "x". Далее мы должны возвести каждое число в квадрат и сложить числа в каждом векторе. Представьте, что вы возводите в квадрат каждое число по горизонтали и складываете их по обоим векторам.
Возьмите квадратный корень из обеих сумм, затем перемножьте их и назовите этот результат "y". Мы находим значение косинуса расстояния как "x", деленное на "y".
Косинусное сходство в основном используется в NLP-приложениях. Главное, что измеряет косинусное сходство, - это разница в семантической ориентации. Если вы работаете с нормализованными векторами, косинусное сходство эквивалентно внутреннему произведению.
Внутреннее произведение - это проекция одного вектора на другой. Величина внутреннего произведения - это вытянутая длина вектора. Чем больше угол между двумя векторами, тем меньше внутреннее произведение. Оно также увеличивается с ростом длины меньшего вектора. Поэтому мы используем внутреннее произведение, когда нам важны ориентация и расстояние. Например, вам нужно пройти по прямой через стены к холодильнику.
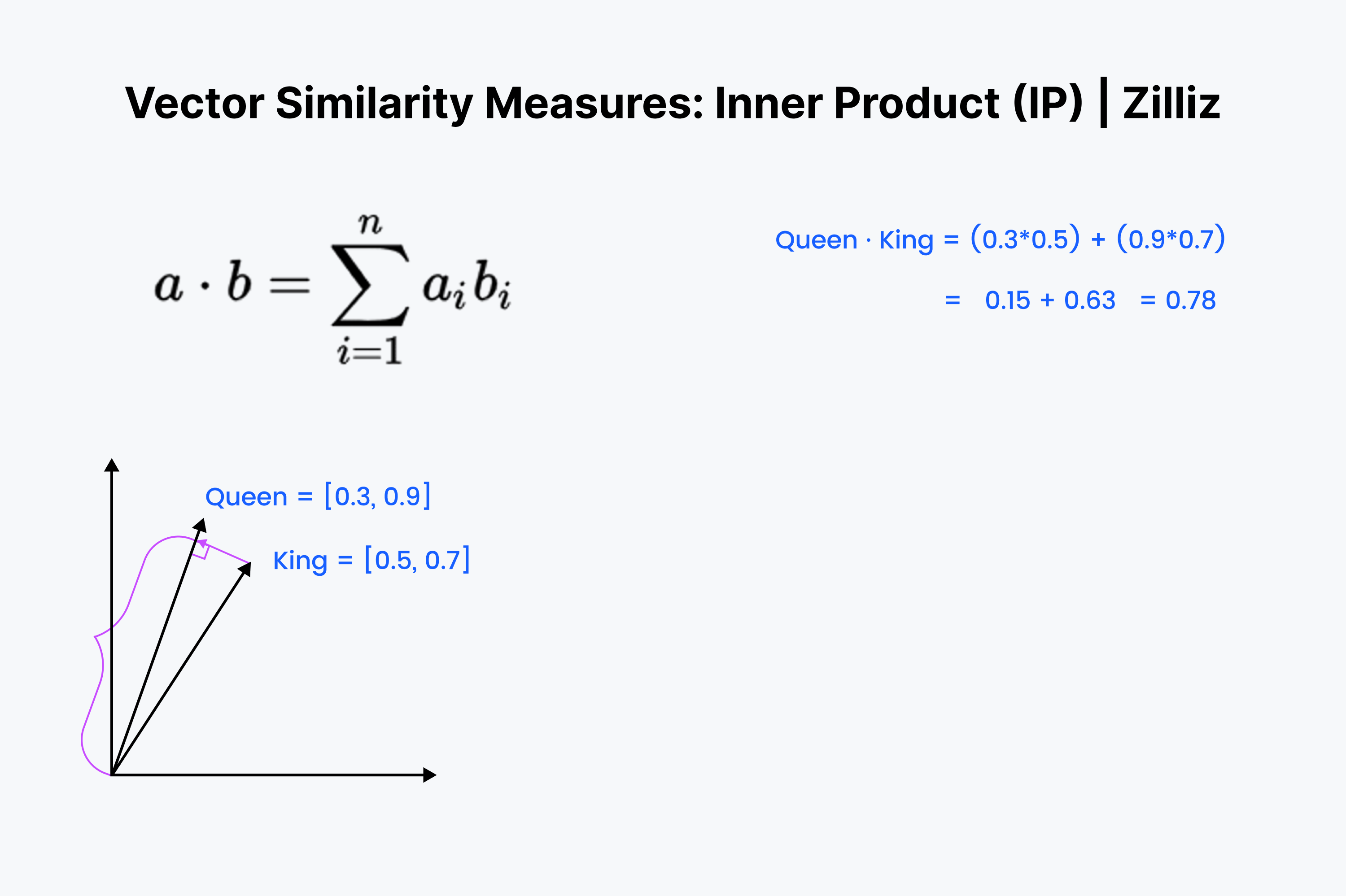
Внутреннее произведение должно выглядеть знакомо. Это всего лишь первая ⅓ вычисления косинуса. Мысленно выстройте эти векторы в ряд и пройдитесь по ряду, умножая в сторону уменьшения. Затем просуммируйте их. Это измеряет расстояние по прямой между вами и ближайшей диммой.
Внутреннее произведение - это нечто среднее между евклидовым расстоянием и косинусным сходством. Когда речь идет о нормализованных наборах данных, оно совпадает с косинусным сходством, поэтому IP подходит как для нормализованных, так и для ненормализованных наборов данных. Это более быстрый вариант, чем косинусное сходство, и более гибкий.
При использовании Inner Product следует помнить, что он не следует неравенству треугольника. Приоритет отдается большим длинам (большим величинам). Это означает, что нужно быть осторожным при использовании IP с Inverted File Index или графовым индексом, например HNSW.
Три векторные метрики, упомянутые выше, наиболее полезны в отношении vector embeddings. Однако это не единственные способы измерения расстояния между двумя векторами. Вот еще два способа измерения расстояния или сходства между векторами.
Group 13401.png
Расстояние Хэмминга можно применять как к векторам, так и к строкам. Для наших случаев будем придерживаться векторов. Расстояние Хэмминга измеряет "разницу" в вхождениях двух векторов. Например, "1011" и "0111" имеют расстояние Хэмминга, равное 2.
С точки зрения векторных вкраплений, расстояние Хэмминга имеет смысл измерять только для бинарных векторов. Float vector embeddings, выходы предпоследнего слоя нейронных сетей, состоят из чисел с плавающей точкой от 0 до 1. Примерами могут служить [0.24, 0.111, 0.21, 0.51235] и [0.33, 0.664, 0.125152, 0.1].
Как видите, расстояние Хэмминга между двумя векторными вложениями почти всегда будет равняться длине самого вектора. Просто существует слишком много возможностей для каждого значения. Именно поэтому расстояние Хэмминга можно применять только к двоичным или разреженным векторам. Такие векторы получаются в результате таких процессов, как TF-IDF, BM25 или SPLADE.
Расстояние Хэмминга хорошо подходит для измерения таких параметров, как разница в формулировках двух текстов, разница в написании слов или разница между любыми двумя двоичными векторами. Но оно не годится для измерения разницы между векторными вкраплениями.
Вот интересный факт. Расстояние Хэмминга эквивалентно суммированию результата операции XOR над двумя векторами.
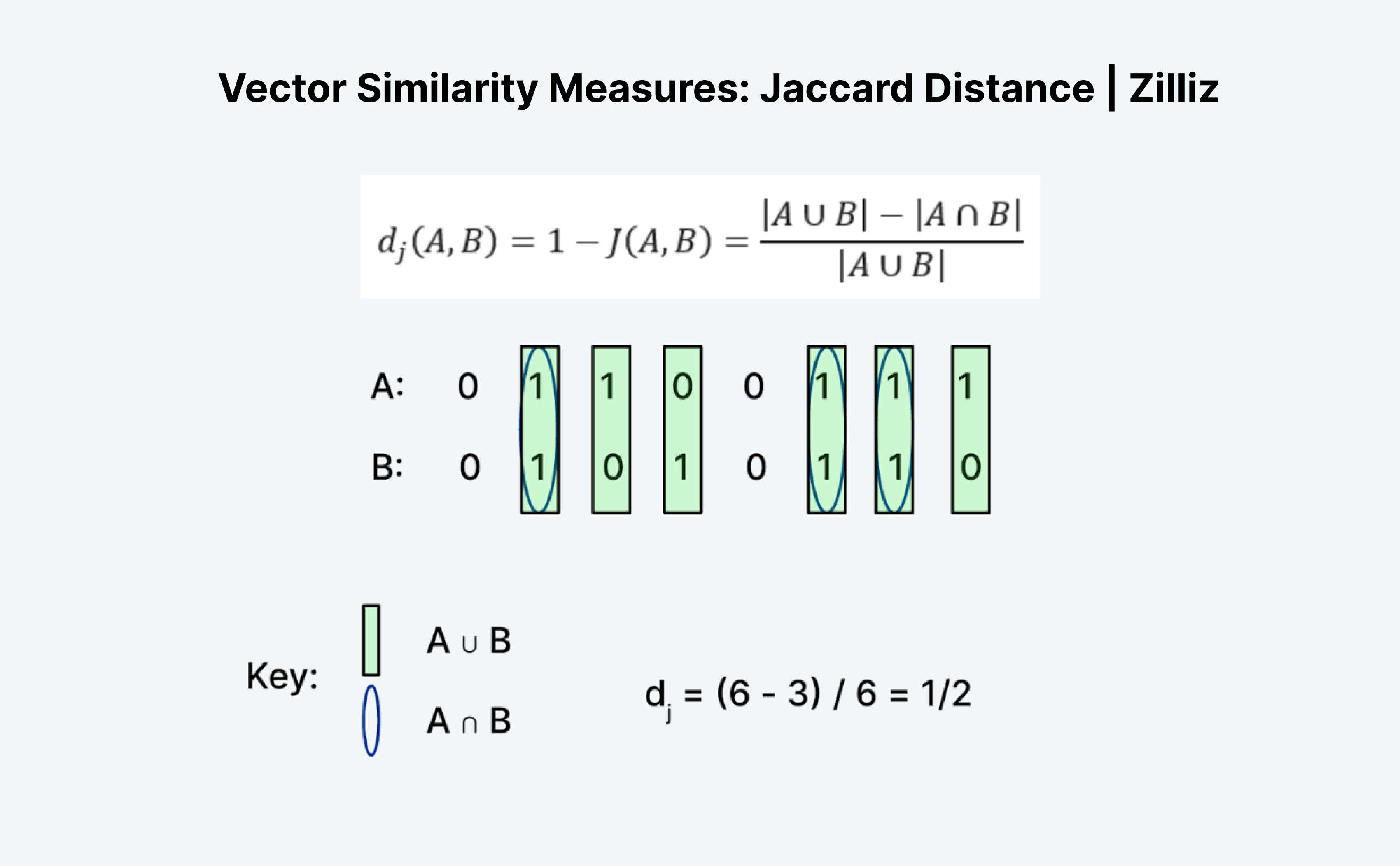
Расстояние Жаккара - это еще один способ измерения сходства или расстояния между двумя векторами. Интересно то, что существует как индекс Жаккара, так и расстояние Жаккара. Расстояние Жаккара равно 1 минус индекс Жаккара, метрика расстояния, которую реализует Milvus.
Вычисление расстояния или индекса Жаккара - интересная задача, потому что на первый взгляд она не совсем логична. Как и расстояние Хэмминга, Жаккард работает только с двоичными данными. Традиционное формирование "союзов" и "пересечений" кажется мне запутанным. Я думаю об этом на примере логики. По сути, это A "OR" B минус A "AND" B, деленное на A "OR" B.
Как показано на рисунке выше, мы считаем количество записей, где либо A, либо B равны 1, как "объединение", а где и A, и B равны 1, как "пересечение". Таким образом, индекс Жаккара для A (01100111) и B (01010110) равен ½. В этом случае расстояние Жаккара, 1 минус индекс Жаккара, также равно ½.
В этом посте мы узнали о трех наиболее полезных метриках поиска векторного сходства: L2 (также известное как евклидово) расстояние, косинусное расстояние и внутреннее произведение. Каждая из этих метрик имеет различные варианты использования. Евклидово расстояние - это когда нам важна разница в величине. Косинус - когда нам важна разница в ориентации. Внутреннее произведение используется, когда нам важна разница в величине и ориентации.
Посмотрите эти видео, чтобы узнать больше о метрике векторного сходства, или read the docs, чтобы узнать, как настроить эти метрики в Milvus.
Введение в метрику сходства
Метрики сходства - важнейший инструмент в различных задачах анализа данных и машинного обучения. Они позволяют сравнивать и оценивать сходство между различными фрагментами данных, облегчая такие приложения, как кластеризация, классификация и рекомендации. Поскольку существует множество метрик сходства, каждая из которых имеет свои сильные и слабые стороны, выбор правильной метрики для конкретной задачи может оказаться непростой задачей. В этом разделе мы представим концепцию метрик сходства, их важность и сделаем обзор наиболее часто используемых метрик.
Косинусное сходство
Косинусное сходство - это широко используемая метрика сходства, которая измеряет косинус угла между двумя векторами. Она широко используется в задачах обработки естественного языка и информационного поиска. Косинусная метрика сходства особенно полезна при работе с высокоразмерными данными, поскольку она эффективна с вычислительной точки зрения и может работать с разреженными данными. Косинусное сходство между двумя векторами может быть рассчитано с помощью точечного произведения векторов, деленного на произведение их величин.
Евклидово расстояние
Евклидово расстояние, также известное как расстояние по прямой, - это широко используемая метрика расстояния, которая измеряет расстояние между двумя точками в n-мерном пространстве. Оно вычисляется как квадратный корень из суммы квадратов разностей между соответствующими элементами двух векторов. Евклидово расстояние широко используется в различных приложениях, включая кластеризацию, классификацию и регрессионный анализ. Однако оно может быть чувствительно к выбросам и плохо работать с высокоразмерными данными.
Выбор правильной метрики сходства
Выбор правильной метрики сходства зависит от различных факторов, включая тип данных, цели анализа и связь между переменными. Например, косинусоидальное сходство подходит для высокоразмерных данных и задач обработки естественного языка, а евклидово расстояние обычно используется для задач кластеризации и классификации. Манхэттенское расстояние, также известное как расстояние L1, подходит для данных с выбросами, а расстояние Хэмминга - для бинарных данных. Важно понимать характеристики и ограничения каждой метрики сходства, чтобы выбрать наиболее подходящую для конкретной задачи.
Применение в реальном мире
Метрики сходства имеют множество реальных применений в различных областях, включая:
Обработка естественного языка: Косинусное сходство широко используется в задачах классификации текстов, анализа настроения и информационного поиска.
Рекомендательные системы: Метрики сходства, такие как косинусоидальное сходство и евклидово расстояние, используются для рекомендации продуктов или услуг на основе поведения и предпочтений пользователей.
Анализ изображений и видео: Метрики сходства, такие как евклидово расстояние и манхэттенское расстояние, используются в задачах классификации изображений и видео, [обнаружения объектов] (https://zilliz.com/learn/what-is-object-detection) и отслеживания.
Кластеризация и классификация: Метрики сходства, такие как евклидово расстояние и косинусное сходство, используются в задачах кластеризации и классификации для объединения схожих точек данных в группы.
В заключение следует отметить, что метрики сходства являются важнейшим инструментом в различных задачах анализа данных и машинного обучения. Понимание характеристик и ограничений каждой метрики сходства необходимо для выбора наиболее подходящей для конкретной задачи. Выбрав правильную метрику сходства, мы сможем повысить точность и релевантность наших результатов, что приведет к принятию более эффективных решений.
Yujian TangYujian Tang is a Developer Advocate at Zilliz. He has a background as a software engineer working on AutoML at Amazon. Yujian studied Computer Science, Statistics, and Neuroscience with research papers published to conferences including IEEE Big Data. He enjoys drinking bubble tea, spending time with family, and being near water.
- Введение в метрику сходства
- Косинусное сходство
- Евклидово расстояние
- Выбор правильной метрики сходства
- Применение в реальном мире
Контент
Начните бесплатно, масштабируйтесь легко
Попробуйте полностью управляемую векторную базу данных, созданную для ваших GenAI приложений.
Попробуйте Zilliz Cloud бесплатноЧитать далее
Zilliz Cloud Update: Tiered Storage, Business Critical Plan, Cross-Region Backup, and Pricing Changes
This release offers a rebuilt tiered storage with lower costs, a new Business Critical plan for enhanced security, and pricing updates, among other features.
Smarter Autoscaling in Zilliz Cloud: Always Optimized for Every Workload
With the latest upgrade, Zilliz Cloud introduces smarter autoscaling—a fully automated, more streamlined, elastic resource management system.
Vector Databases vs. Document Databases
Use a vector database for similarity search and AI-powered applications; use a document database for flexible schema and JSON-like data storage.