Flajolet-Martin Algorithm: Scalable Cardinality Estimation in Data Streams
Flajolet-Martin Algorithm: Scalable Cardinality Estimation in Data Streams
Accurately counting unique visitors, distinct IP addresses, or diverse search queries is essential for organizations looking to gain meaningful insights. However, tracking every single data point can be resource-intensive, slowing down real-time analysis. Traditional methods, such as maintaining hash sets, require heavy computation and memory, making them impractical as data grows.
Figure 1 Visualization of Data Stream and Hashing
Figure 1: Visualization of Data Stream and Hashing
The Flajolet-Martin algorithm effectively solves this issue. It estimates distinct element counts in extensive data flows through efficient operations while minimizing memory requirements and delivering accurate results.
The algorithm uses hash functions to analyze patterns in hashed values to estimate uniqueness instead of explicitly tracking each entity. This method reduces memory requirements, enabling quick processing and real-time analytical capabilities.
Organizations using the Flajolet-Martin algorithm obtain real-time scalability for monitoring and analytics. This enables them to make quick decisions at lower costs than traditional counting methods. Its memory-efficient design makes it well-suited for data-intensive environments, balancing accuracy and performance without the overhead of storing every individual data point.
In this piece, we will explain the FMA algorithm's concept, workings, and main use cases. We will also see how it can benefit individuals or organizations and what challenges will arise while implementing it.
What is the Flajolet-Martin Algorithm?
The Flajolet-Martin algorithm is a probabilistic approach to evaluating the distinct element count (cardinality) within large datasets or streaming information. Philippe Flajolet and G. Nigel Martin introduced the algorithm in 1984 to solve situations where exact counting becomes impractical because of memory or computational limitations.
The algorithm offers maximum memory efficiency through its approximation technique. This helps analyze large datasets under time-sensitive real-time conditions. Unlike deterministic methods that require extensive storage, its probabilistic approach significantly reduces memory consumption while maintaining efficiency. This makes it well-suited for large-scale data processing.
The algorithm's approximation method trades exact precision for faster data processing while reducing computational costs. This allows organizations to analyze and respond to data-driven insights within near real-time operations using minimal resources.
How the Flajolet-Martin Algorithm Works
The Flajolet-Martin algorithm employs probabilistic techniques to efficiently estimate the number of unique elements in large datasets. The fundamental principle uses hash function randomness to create an efficient cardinality approximation method, eliminating the need to maintain extensive data structures or exact counts. Here is how it works:
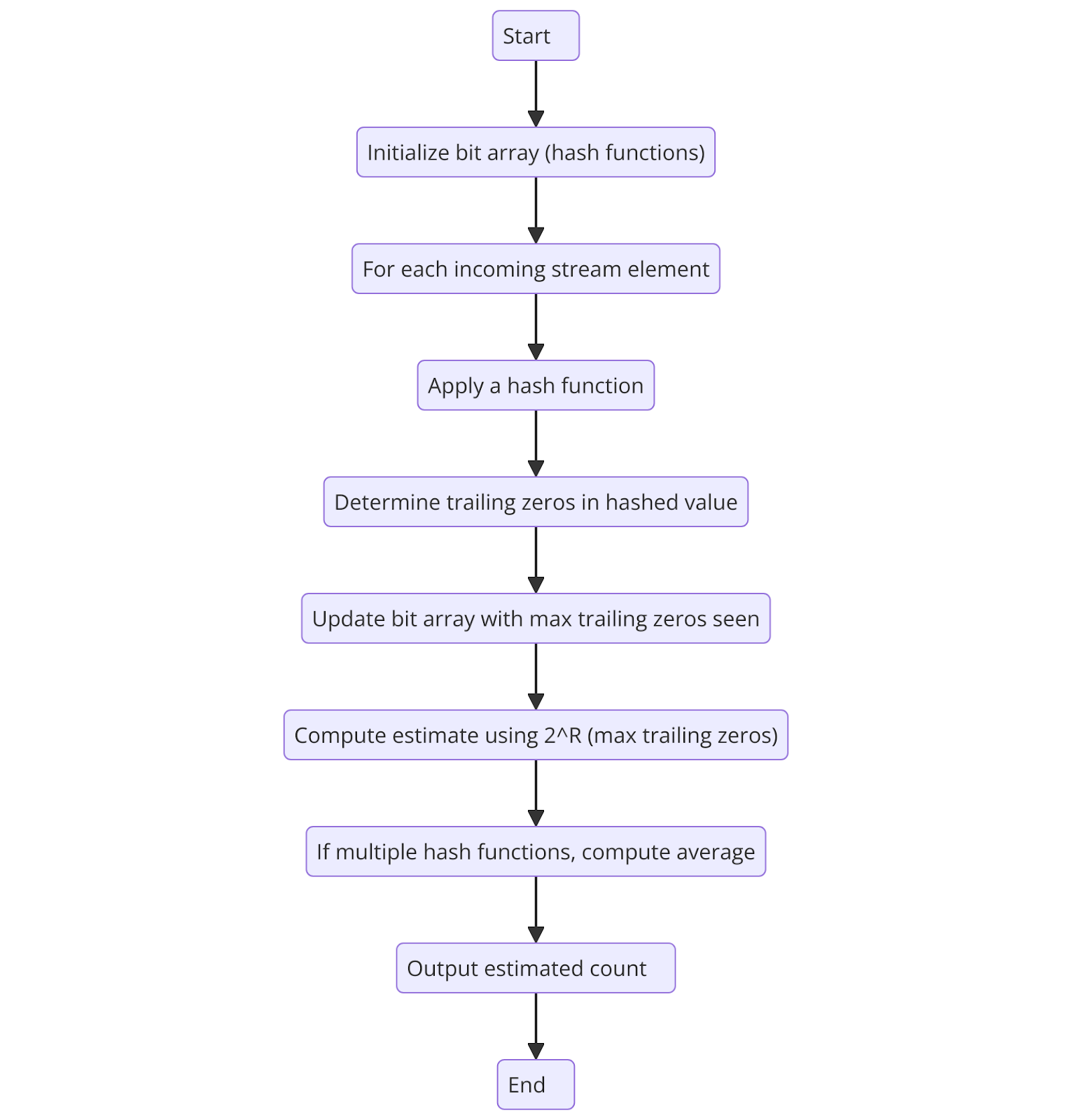Figure 2 Flowchart of the Flajolet-Martin Algorithm
Figure 2: Flowchart of the Flajolet-Martin Algorithm
Hashing the Input
The hash function processes incoming elements into randomly distributed binary numbers. The uniform distribution method ensures that each bit has an equal probability of being '0' or '1'. This maximizes randomness in the hashing process. A well-designed hash function is crucial for minimizing collisions, improving accuracy, and ensuring reliable cardinality estimates.
Identifying Trailing Zeros
The algorithm determines trailing zero counts for each hashed value by starting from the right side (least significant bit) until it reaches the first '1'. These trailing zero counts reflect the probability distribution of the hashed values. The Flajolet-Martin algorithm estimates the number of distinct values by counting the trailing zeros in the hashed numbers of elements.
Higher maximum trailing zero counts indicate greater cardinality. An estimate of distinct elements is calculated by raising 2 to the power of the maximum trailing zero count. The algorithm relies on binary hash functions to generate precise cardinality estimates using minimal memory resources.
Recording Maximum Trailing Zeros
The algorithm tracks the maximum number of trailing zeros that appear in any hashed value rather than monitoring all dataset elements. The appearance of additional unique elements in the dataset raises the probability that hashed values with longer trailing zero sequences will be observed.
The statistical distribution of trailing zeros enables the algorithm to derive an indirect measurement of unique element count. The algorithm works best for streaming data and large-scale operations because it does not store individual data items. This design ensures excellent memory efficiency and enables fast processing speed.
Estimating Cardinality
The algorithm determines unique element counts through this essential mathematical expression:
E = 2R
where:
- R is the highest number of trailing zeros observed among all hashed values.
The probability-based logic suggests that datasets with more distinct elements produce hashed values that end with numerous trailing zeros.
The algorithm estimates dataset distinct elements by assuming values with at least trailing zeros occur about once per element. The method is fast for estimating large data counts while eliminating the need to store all individual items.
Comparison
It's useful to compare the Flajolet-Martin algorithm with other methods to see how it measures up. How accurate is it? How much memory does it need? How fast does it process data? These factors help determine its effectiveness.
| Feature | Flajolet-Martin | HyperLogLog | Count-Min Sketch |
| Primary Use Case | Estimating the number of distinct elements (cardinality) in large datasets or streams. | Improved accuracy in cardinality estimation with reduced memory usage. | Estimating the frequency of elements in data streams, identifying heavy hitters. |
| Memory Usage | Requires sublinear space, specifically O(log log n) bits, where n is the number of distinct elements. | Optimized to use O(log log n) bits; for example, counting billions of distinct items with ~2% error can be achieved with approximately 1.5 kilobytes of memory. | Utilizes O(w × d) space, where w is the width and d is the depth of the sketch; typically requires kilobytes to a few megabytes, depending on desired accuracy and input size. |
| Accuracy | Provides an estimate with a standard error; accuracy improves with more hash functions and larger bitmaps. | Offers high accuracy with a standard error of approximately 1.04/√m, where m is the number of registers used. | May overestimate frequencies due to hash collisions; accuracy depends on the number of hash functions and the sketch size. |
| Time Complexity | Processes each element in constant time, O(1), making it suitable for high-speed data streams. | Constant time, O(1), per element for insertion and query operations. | Constant time, O(1), per update and query; efficiency depends on the number of hash functions and sketch dimensions. |
| Handling Duplicates | Naturally, it accounts for duplicates; each unique element contributes to the estimate based on its hashed value. | Effectively handles duplicates; multiple occurrences of the same element do not affect the cardinality estimate. | Records the frequency of elements, so duplicates increase the count for that element. |
| Mergeability | It supports merging multiple FM sketches to combine estimates from different data streams. | Easily mergeable; multiple HyperLogLog structures can be combined to produce an aggregate estimate. | Mergeable by element-wise summation of corresponding counters from different sketches. |
| Use in Industry | Foundational algorithms lead to more advanced structures like HyperLogLog, which are used in network traffic analysis and large-scale data processing. | Widely adopted in systems like Redis, Apache Druid, and Google BigQuery for efficient cardinality estimation. | Utilized in applications requiring frequency estimation, such as network monitoring, natural language processing, and database systems. |
Benefits and Challenges
While the flajolet-martin algorithm offers various benefits, it also comes with challenges. Let’s uncover both the benefits and challenges:
Benefits
Memory efficiency: The algorithm attains its efficiency through hash functions and bit manipulation techniques, which optimize data representation.
Single-pass processing: The algorithm estimates unique counts in just one pass through the data. This makes it ideal for real-time analytics.
Scalability: The Flajolet-Martin algorithm demonstrates natural scalability because it processes large datasets using minimal memory resources due to its logarithmic space complexity.
Applicability to big data analytics: The algorithm demonstrates strong applicability to big data analytics through its efficient and scalable design. This enables quick, unique element approximations.
Foundation for advanced algorithms: The Flajolet-Martin algorithm is a fundamental base for developing advanced cardinality estimation algorithms, including HyperLogLog, which delivers higher accuracy.
Challenges
Variance in estimates: The algorithm demonstrates high estimate variance. This requires multiple hash function runs to produce accurate results.
Sensitivity to hash function selection: Inadequate hash function selection produces incorrect results because the algorithm requires hash values to distribute uniformly for optimal performance.
Limited to cardinality estimation: The algorithm functions exclusively for cardinality estimation because it determines the number of distinct items but fails to identify individual elements or their occurrence counts.
Applicability constraints: The algorithm proves effective for large datasets, yet it becomes less appropriate when working with small datasets.
Implementation complexity: Adoption of the Flajolet-Martin algorithm becomes harder because experts who understand hash functions and probabilistic counting methods need to be trained.
Use Cases and Tools
Now that we understand the Flajolet-Martin algorithm's benefits and challenges, let's discuss its real-world applications. We'll also look at the key tools that help implement it effectively.
Use Cases
FMA demonstrates its effectiveness through several application scenarios that include:
Web analytics: Websites frequently need to estimate their unique visitor numbers while avoiding the storage of personal user information. The FMA method delivers memory-efficient calculations to estimate visitor counts, thus helping websites track site usage and user interaction.
Network monitoring: Network security depends on identifying the exact number of unique IP addresses accessing the network. This detection helps identify security threats and anomalies. FMA delivers real-time calculations of distinct IP addresses, which helps organizations detect and respond rapidly to abnormal network behavior.
Database management: Databases execute regular operations to count the entries within their columns. FMA provides rapid count estimation, which helps databases optimize their query planning and resource management processes.
Big data processing: Big data environments need algorithms to process continuous data streams through limited memory resources during data stream analysis. FMA functions as part of the Apache Spark and Flink frameworks to deliver high-efficiency real-time streaming data analytics.
Real-time processing: Applications such as financial tickers, social media feeds, and sensor networks create data that requires instant processing. FMA delivers rapid estimates of unique elements, making it an essential tool for instant decision-making applications.
Tools
Multiple tools alongside libraries exist to implement Flajolet-Martin’s algorithm and its variants, simplifying system integration. These include:
Apache DataSketches: The open-source library DataSketches provides multiple stochastic streaming algorithms, including Flajolet-Martin-based algorithms for approximate data analysis. The Flajolet-Martin algorithm finds wide application in real-time systems that process and analyze massive data streams, including telemetry systems and network monitoring operations.
PostgreSQL Flajolet-Martin Extension: The PostgreSQL Flajolet-Martin extension adds algorithm-based functions to PostgreSQL databases, enabling users to execute approximate distinct count operations through SQL queries. This extension benefits database performance by delivering quick, unique value estimations in large tables without the need for exact calculations.
Python Implementation by ApoorvaSaxena1: A Python-based implementation of the Flajolet-Martin algorithm showcases its ability to estimate the number of distinct items in streaming data.
Probabilistic Counting with Stochastic Averaging: The algorithm PCSA employs bitmaps to track trailing zeros in hashed values, which enables stream unique element estimation.
FAQs
What problem does the Flajolet-Martin algorithm solve efficiently?
The Flajolet-Martin algorithm estimates unique elements in large data streams while discarding the need to store all aspects. The algorithm performs efficient estimation with sublinear space requirements, making it appropriate for network monitoring, database queries, and web analytics applications.
How does the algorithm handle duplicate values in a stream?
The algorithm keeps track of the rightmost 1-bit in hashed values, which helps detect repeated occurrences without storing the full list. This approach ensures an accurate estimate of unique counts while automatically filtering out duplicates in data streams with a lot of repetition.
Can the Flajolet-Martin algorithm be used for real-time analytics?
The algorithm is suitable for real-time data processing because it streams data while needing only minimal memory resources. Practical applications include website traffic monitoring, active user counting on platforms, network connection identification, and hashtag tracking on social media platforms.
What are the main limitations of the Flajolet-Martin algorithm?
It shows reduced effectiveness when hash functions produce errors or when the data distribution is unbalanced. The algorithm faces difficulties processing highly skewed data but requires stochastic averaging methods to achieve accurate results without increasing memory consumption.
How does the algorithm compare to HyperLogLog?
The advanced version of Flajolet-Martin, HyperLogLog, implements improved statistical methods and advanced data structures to enhance estimation quality. The technique decreases errors without compromising its memory-efficient design.
Related Resources
- What is the Flajolet-Martin Algorithm?
- How the Flajolet-Martin Algorithm Works
- Comparison
- Benefits and Challenges
- Use Cases and Tools
- FAQs
- Related Resources
Content
Start Free, Scale Easily
Try the fully-managed vector database built for your GenAI applications.
Try Zilliz Cloud for Free