Métricas de similitud para la búsqueda vectorial
Métricas de similitud vectorial para la búsqueda - Zilliz Blog
No se pueden comparar manzanas y naranjas. ¿O sí? Las bases de datos vectoriales como Milvus te permiten comparar cualquier dato que puedas vectorizar. Incluso puedes hacerlo directamente en tu Jupyter Notebook. Pero, ¿cómo funciona la búsqueda de similitud vectorial?
La búsqueda vectorial tiene dos componentes conceptuales críticos: índices y métricas de distancia. Algunos índices vectoriales populares son HNSW, IVF y ScaNN. Existen tres métricas de distancia principales: L2 o distancia euclidiana, similitud coseno y producto interior. La distancia Manhattan calcula la distancia entre puntos sumando las diferencias absolutas en cada dimensión y es ventajosa en escenarios en los que es necesario minimizar la sensibilidad a los valores atípicos. Otras métricas para vectores binarios son la distancia de Hamming y el índice de Jaccard.
En este artículo trataremos:
Métricas de similitud de vectores
L2 o Euclídea
¿Cómo funciona la distancia L2?
¿Cuándo utilizar la distancia euclídea?
Coseno de similitud
¿Cómo funciona la similitud coseno?
¿Cuándo se debe utilizar la similitud del coseno?
Producto interior
¿Cómo funciona el producto interior?
¿Cuándo debe utilizar el Producto Interior?
Otras métricas interesantes de similitud o distancia vectorial
Distancia Hamming
Índice de Jaccard
Resumen de métricas de búsqueda de similitud vectorial
Los vectores pueden representarse como listas de números o como una orientación y una magnitud. Para entenderlo de la forma más sencilla, puede imaginar los vectores como segmentos de línea que apuntan en direcciones específicas en el espacio.
La métrica L2 o euclídea es la métrica de la "hipotenusa" de dos vectores. Mide la magnitud de la distancia entre donde terminan las líneas de sus vectores.
La similitud coseno es el ángulo entre sus líneas donde se encuentran.
El producto interior es la "proyección" de un vector sobre el otro. Intuitivamente, mide tanto la distancia como el ángulo entre los vectores.
La métrica de distancia más intuitiva es L2 o distancia euclídea. Podemos imaginarla como la cantidad de espacio entre dos objetos. Por ejemplo, la distancia entre tu pantalla y tu cara.
Ya hemos imaginado cómo funciona la distancia L2 en el espacio; ¿cómo funciona en matemáticas? Empecemos imaginando ambos vectores como una lista de números. Alinea las listas una encima de otra y réstalas hacia abajo. A continuación, eleva al cuadrado todos los resultados y súmalos. Por último, saca la raíz cuadrada.
Milvus se salta la raíz cuadrada porque el orden de rango con raíz cuadrada y sin raíz cuadrada es el mismo. De este modo, podemos omitir una operación y obtener el mismo resultado, reduciendo la latencia y el coste y aumentando el rendimiento. A continuación se muestra un ejemplo de cómo funciona la distancia euclídea o L2.
d(Reina, Rey) = √(0,3-0,5)2 + (0,9-0,7)2
= √(0.2)2 + (0.2)2
= √0.04 + 0.04
= √0.08 ≅ 0.28
Una de las principales razones para utilizar la [distancia] euclídea es cuando tus vectores](https://zilliz.com/glossary/vector-distance) tienen magnitudes diferentes. Principalmente te importa lo lejos que están tus palabras en el espacio o distancia semántica.
Utilizamos el término "similitud coseno" o "distancia coseno" para denotar la diferencia entre la orientación de dos vectores. Por ejemplo, ¿a qué distancia te girarías para mirar hacia la puerta principal?
Dato divertido y aplicable: a pesar de que "similitud" y "distancia" tienen significados diferentes por sí solos, ¡añadir coseno delante de ambos términos hace que signifiquen casi lo mismo! Este es otro ejemplo de similitud semántica en juego.
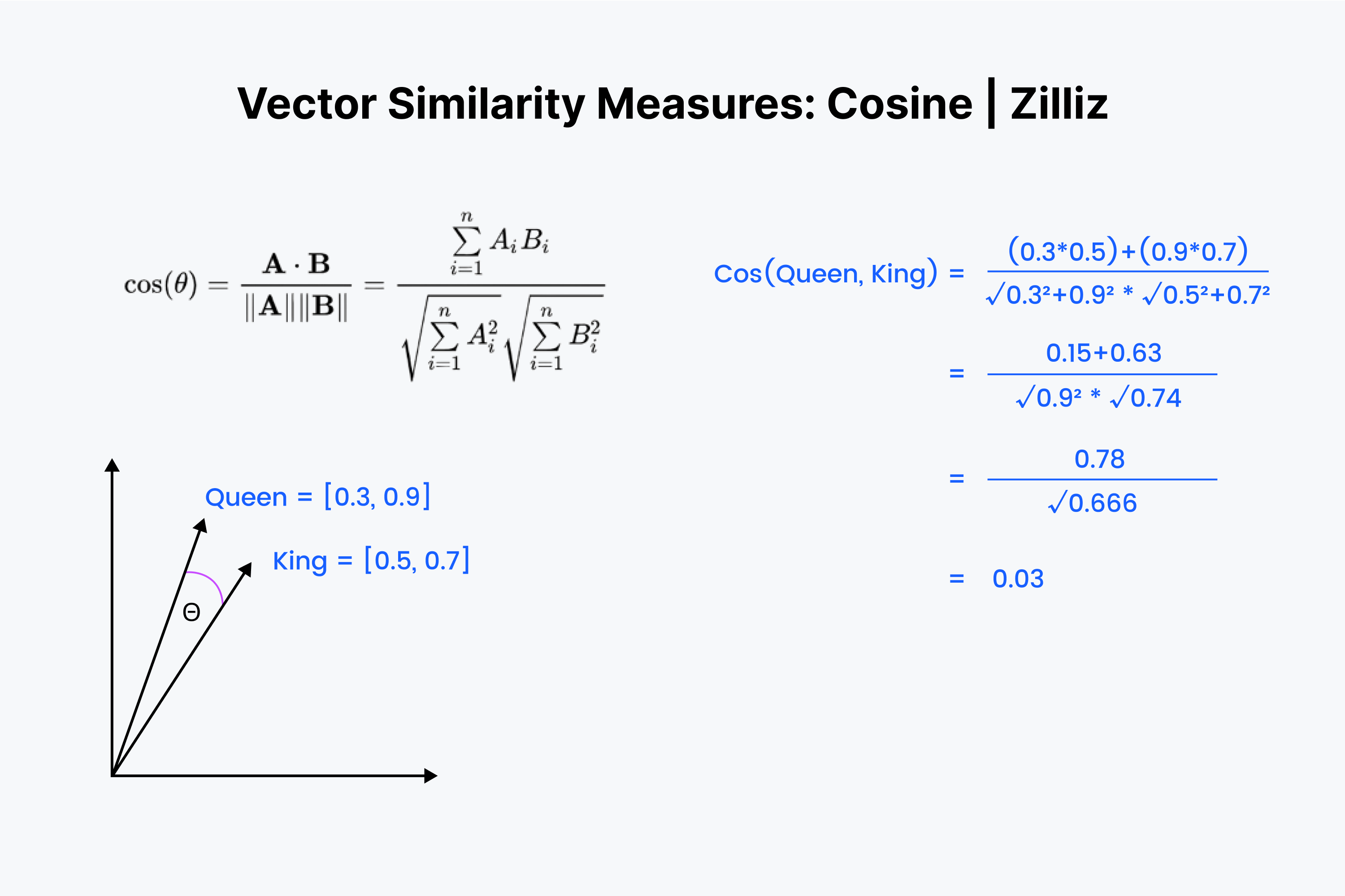
Sabemos que la similitud coseno mide el ángulo entre dos vectores. Una vez más, imaginamos nuestros vectores como una lista de números. Pero esta vez el proceso es un poco más complejo.
Empezamos de nuevo alineando los vectores uno encima de otro. Empieza multiplicando los números y sumando todos los resultados. Ahora guarda ese número; llámalo "x". A continuación, debemos elevar al cuadrado cada número y sumar los números de cada vector. Imagina que elevas al cuadrado cada número horizontalmente y los sumas para ambos vectores.
Saca la raíz cuadrada de ambas sumas, multiplícalas y llama a este resultado "y". Hallamos el valor de nuestra distancia coseno como "x" dividido por "y".
La similitud coseno se utiliza principalmente en aplicaciones de PNL. Lo principal que mide la similitud coseno es la diferencia de orientación semántica. Si se trabaja con vectores normalizados, la similitud coseno es equivalente al producto interior.
El producto interior es la proyección de un vector sobre otro. El valor del producto interior es la longitud extraída del vector. Cuanto mayor sea el ángulo entre los dos vectores, menor será el producto interior. También aumenta con la longitud del vector más pequeño. Por lo tanto, utilizamos el producto interior cuando nos preocupamos por la orientación y la distancia. Por ejemplo, tendrías que recorrer una distancia recta a través de las paredes hasta tu frigorífico.
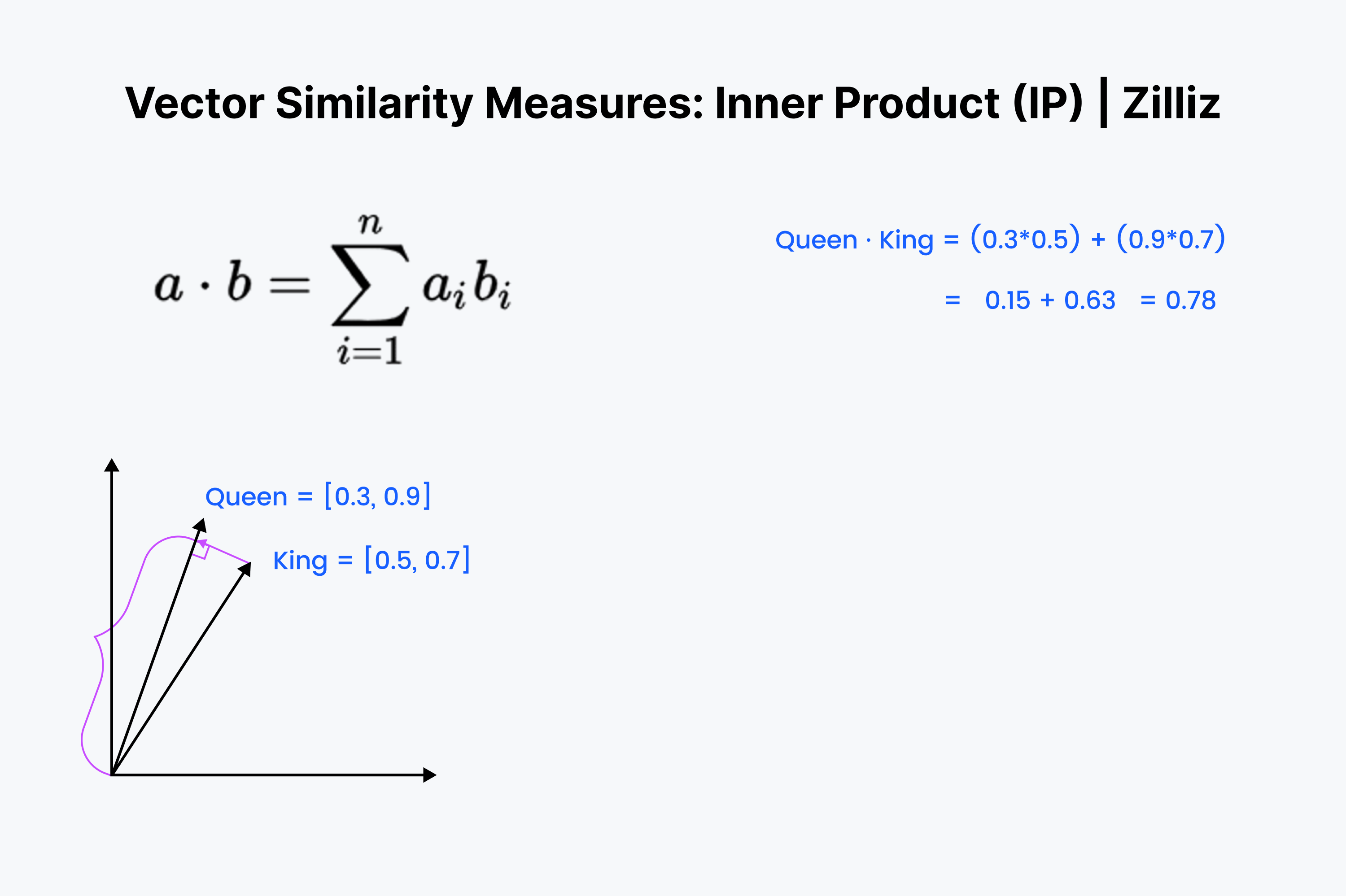
El producto interior debería resultarte familiar. Es sólo el primer ⅓ del cálculo del coseno. Alinea esos vectores en tu mente y baja por la fila, multiplicando hacia abajo. Luego, súmalos. Esto mide la distancia en línea recta entre tú y la suma dim más cercana.
El producto interior es como un cruce entre la distancia euclidiana y la similitud coseno. Cuando se trata de conjuntos de datos normalizados, es lo mismo que la similitud coseno, por lo que el PI es adecuado para conjuntos de datos normalizados o no normalizados. Es una opción más rápida que la similitud coseno y más flexible.
Una cosa a tener en cuenta con el Producto Interior es que no sigue la desigualdad del triángulo. Se da prioridad a las longitudes mayores (magnitudes grandes). Esto significa que debemos tener cuidado cuando utilicemos IP con Inverted File Index o un índice gráfico como HNSW.
Las tres métricas vectoriales mencionadas anteriormente son las más útiles en relación con vector embeddings. Sin embargo, no son las únicas formas de medir la distancia entre dos vectores. He aquí otras dos formas de medir la distancia o similitud entre vectores.
Grupo 13401.png](https://assets.zilliz.com/Group_13401_dc84119c7f.png)
La distancia de Hamming puede aplicarse a vectores o cadenas. Para nuestros casos de uso, vamos a ceñirnos a los vectores. La distancia de Hamming mide la "diferencia" entre las entradas de dos vectores. Por ejemplo, "1011" y "0111" tienen una distancia Hamming de 2.
En términos de incrustación de vectores, la distancia Hamming sólo tiene sentido para vectores binarios. Los Float vector embeddings, las salidas de la penúltima capa de las redes neuronales, se componen de números de coma flotante entre 0 y 1. Algunos ejemplos son [0,24, 0,111, 0,21, 0,51235] y [0,33, 0,664, 0,125152, 0,1].
Como se puede ver, la distancia de Hamming entre dos incrustaciones vectoriales casi siempre será igual a la longitud del propio vector. Hay demasiadas posibilidades para cada valor. Por eso la distancia de Hamming sólo puede aplicarse a vectores binarios o dispersos. El tipo de vectores que se producen a partir de un proceso como TF-IDF, BM25 o SPLADE.
La distancia de Hamming es buena para medir algo como la diferencia de redacción entre dos textos, la diferencia en la ortografía de las palabras o la diferencia entre dos vectores binarios cualesquiera. Pero no es buena para medir la diferencia entre incrustaciones de vectores.
He aquí un dato curioso. La distancia de Hamming equivale a sumar el resultado de una operación XOR sobre dos vectores.
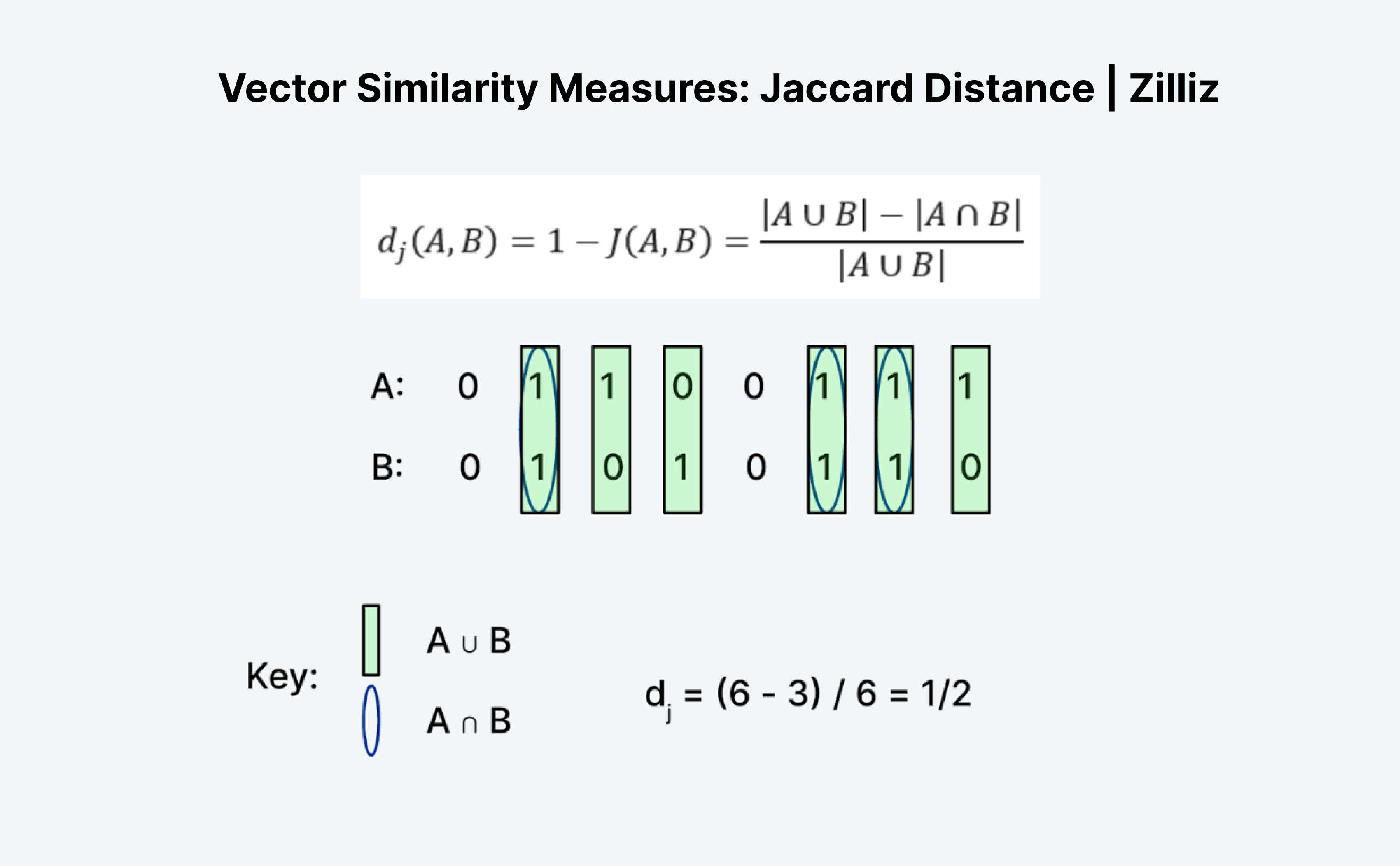
La distancia de Jaccard es otra forma de medir la similitud o distancia de dos vectores. Lo interesante de Jaccard es que existe tanto un índice de Jaccard como una distancia de Jaccard. La distancia de Jaccard es 1 menos el índice de Jaccard, la métrica de distancia que implementa Milvus.
Calcular la distancia o el índice Jaccard es una tarea interesante porque no tiene exactamente sentido a primera vista. Al igual que la distancia Hamming, Jaccard sólo funciona con datos binarios. La formación tradicional de "uniones" e "intersecciones" me parece confusa. La forma en que yo lo veo es con la lógica. Es esencialmente A "O" B menos A "Y" B dividido por A "O" B.
Como se muestra en la imagen de arriba, contamos el número de entradas donde A o B es 1 como la "unión" y donde ambos A y B son 1 como la "intersección". Así pues, el índice de Jaccard para A (01100111) y B (01010110) es ½. En este caso, la distancia de Jaccard, 1 menos el índice de Jaccard, también es ½.
En este post, aprendimos sobre las tres métricas de búsqueda de similitud vectorial más útiles: La distancia L2 (también conocida como euclidiana), la distancia coseno y el producto interior. Cada una de ellas tiene diferentes casos de uso. La euclídea es para cuando nos importa la diferencia de magnitud. El coseno es para cuando nos importa la diferencia de orientación. El producto interior es cuando nos preocupamos por la diferencia en magnitud y orientación.
Vea estos videos para aprender más sobre las métricas de similitud vectorial, o lea los documentos para aprender a configurar estas métricas en Milvus.
Introducción a las métricas de similitud
Las métricas de similitud son una herramienta crucial en varias tareas de análisis de datos y aprendizaje automático. Nos permiten comparar y evaluar la similitud entre distintas piezas de datos, facilitando aplicaciones como la agrupación, la clasificación y las recomendaciones. Con numerosas métricas de similitud disponibles, cada una con sus puntos fuertes y débiles, elegir la adecuada para una tarea específica puede ser todo un reto. En esta sección, introduciremos el concepto de métrica de similitud, su importancia y ofreceremos una visión general de las métricas más utilizadas.
Similitud Coseno
La similitud coseno es una métrica de similitud ampliamente utilizada que mide el coseno del ángulo entre dos vectores. Se utiliza habitualmente en tareas de procesamiento del lenguaje natural y recuperación de información. La métrica de similitud del coseno es particularmente útil cuando se trabaja con datos de alta dimensión, ya que es computacionalmente eficiente y puede manejar datos dispersos. La similitud coseno entre dos vectores puede calcularse utilizando el producto punto de los vectores dividido por el producto de sus magnitudes.
Distancia euclidiana
La distancia euclídea, también conocida como distancia en línea recta, es una métrica de distancia ampliamente utilizada que mide la distancia entre dos puntos en un espacio n-dimensional. Se calcula como la raíz cuadrada de la suma de las diferencias al cuadrado entre los elementos correspondientes de los dos vectores. La distancia euclídea se utiliza habitualmente en diversas aplicaciones, como la agrupación, la clasificación y el análisis de regresión. Sin embargo, puede ser sensible a los valores atípicos y puede no funcionar bien con datos de alta dimensión.
Elegir la métrica de similitud adecuada
La elección de la métrica de similitud adecuada depende de varios factores, como el tipo de datos, los objetivos del análisis y la relación entre las variables. Por ejemplo, la similitud coseno es adecuada para datos de alta dimensión y tareas de procesamiento de lenguaje natural, mientras que la distancia euclidiana se utiliza habitualmente para tareas de agrupación y clasificación. La distancia Manhattan, también conocida como distancia L1, es adecuada para datos con valores atípicos, mientras que la distancia Hamming se utiliza para datos binarios. Es esencial comprender las características y limitaciones de cada métrica de similitud para elegir la más adecuada para una tarea específica.
Aplicaciones reales
Las métricas de similitud tienen numerosas aplicaciones en el mundo real en diversos campos, entre ellos:
Procesamiento del lenguaje natural: La similitud del coseno se utiliza ampliamente en tareas de clasificación de textos, análisis de sentimientos y recuperación de información.
Sistemas de recomendación: Las métricas de similitud, como la similitud coseno y la distancia euclídea, se utilizan para recomendar productos o servicios en función del comportamiento y las preferencias de los usuarios.
Análisis de imágenes y vídeos: Las métricas de similitud, como la distancia euclídea y la distancia Manhattan, se utilizan en tareas de clasificación de imágenes y vídeos, detección de objetos y seguimiento.
Agrupación y clasificación: Las métricas de similitud, como la distancia euclidiana y la similitud coseno, se utilizan en tareas de agrupación y clasificación para agrupar puntos de datos similares.
En conclusión, las métricas de similitud son una herramienta crucial en diversas tareas de análisis de datos y aprendizaje automático. Comprender las características y limitaciones de cada métrica de similitud es esencial para elegir la más adecuada para una tarea específica. Seleccionando la métrica de similitud adecuada, podemos mejorar la precisión y relevancia de nuestros resultados, lo que conduce a una mejor toma de decisiones y conocimientos.
Yujian TangYujian Tang is a Developer Advocate at Zilliz. He has a background as a software engineer working on AutoML at Amazon. Yujian studied Computer Science, Statistics, and Neuroscience with research papers published to conferences including IEEE Big Data. He enjoys drinking bubble tea, spending time with family, and being near water.
- Introducción a las métricas de similitud
- Similitud Coseno
- Distancia euclidiana
- Elegir la métrica de similitud adecuada
- Aplicaciones reales
Contenido
Comienza Gratis, Escala Fácilmente
Prueba la base de datos vectorial completamente gestionada construida para tus aplicaciones GenAI.
Prueba Zilliz Cloud GratisSigue leyendo
Zilliz Cloud Update: Tiered Storage, Business Critical Plan, Cross-Region Backup, and Pricing Changes
This release offers a rebuilt tiered storage with lower costs, a new Business Critical plan for enhanced security, and pricing updates, among other features.
Vector Databases vs. Spatial Databases
Use a vector database for AI-powered similarity search; use a spatial database for geographic and geometric data analysis and querying.
DeepSeek vs. OpenAI: A Battle of Innovation in Modern AI
Compare OpenAI's o1 and o3-mini with DeepSeek R1's open-source alternative. Discover which AI model offers the best balance of reasoning capabilities and cost efficiency.