Metriche di somiglianza per la ricerca vettoriale
Metriche di similarità vettoriale per la ricerca - Blog Zilliz
Non si possono confrontare mele e arance. O forse sì? I database vettoriali come Milvus permettono di confrontare qualsiasi dato che si può vettorializzare. Potete anche farlo direttamente nel vostro Jupyter Notebook. Ma come funziona la ricerca di similarità vettoriale?
La ricerca vettoriale ha due componenti concettuali fondamentali: gli indici e le metriche di distanza. Alcuni popolari indici vettoriali includono HNSW, IVF e ScaNN. Esistono tre metriche di distanza principali: L2 o distanza euclidea, somiglianza coseno e prodotto interno. La distanza di Manhattan calcola la distanza tra i punti sommando le differenze assolute in ogni dimensione ed è vantaggiosa negli scenari in cui è necessario ridurre al minimo la sensibilità agli outlier. Altre metriche per vettori binari includono la distanza di Hamming e l'indice di Jaccard.
In questo articolo tratteremo di:
Metriche di somiglianza vettoriale
L2 o Euclidea
Come funziona la distanza L2?
Quando si dovrebbe usare la distanza euclidea?
Similitudine del coseno
Come funziona la somiglianza cosinica?
Quando si dovrebbe usare la somiglianza del coseno?
Prodotto interno
Come funziona il prodotto interno?
Quando si dovrebbe usare il Prodotto Interno?
Altre interessanti metriche di somiglianza vettoriale o di distanza
Distanza di Hamming
Indice di Jaccard
Sintesi delle metriche di ricerca della somiglianza vettoriale
I vettori possono essere rappresentati come elenchi di numeri o come un orientamento e una grandezza. Per capire meglio, si possono immaginare i vettori come segmenti di linea che puntano in direzioni specifiche nello spazio.
La metrica L2 o euclidea** è la metrica dell'ipotenusa di due vettori. Misura la grandezza della distanza tra i punti in cui finiscono le linee dei vettori.
La simmetria del coseno è l'angolo tra le linee che si incontrano.
Il prodotto interno** è la "proiezione" di un vettore sull'altro. Intuitivamente, misura sia la distanza che l'angolo tra i vettori.
La metrica di distanza più intuitiva è la L2 o distanza euclidea. Possiamo immaginarla come la quantità di spazio tra due oggetti. Ad esempio, la distanza tra il vostro schermo e il vostro viso.
Abbiamo immaginato come funziona la distanza L2 nello spazio; come funziona in matematica? Iniziamo immaginando entrambi i vettori come un elenco di numeri. Allineiamo gli elenchi l'uno sull'altro e sottraiamo verso il basso. Quindi, elevare al quadrato tutti i risultati e sommarli. Infine, si esegue la radice quadrata.
Milvus salta la radice quadrata perché l'ordine di rango con radice quadrata e senza radice quadrata è lo stesso. In questo modo, possiamo saltare un'operazione e ottenere lo stesso risultato, riducendo la latenza e il costo e aumentando il throughput. Di seguito è riportato un esempio di come funziona la distanza euclidea o L2.
d(Regina, Re) = √(0,3-0,5)2 + (0,9-0,7)2
= √(0.2)2 + (0.2)2
= √0.04 + 0.04
= √0.08 ≅ 0.28
Una delle ragioni principali per usare la distanza euclidea è quando i vettori hanno grandezze diverse. Ci si preoccupa soprattutto di quanto le parole siano distanti nello spazio o della distanza semantica.
Si usa il termine "somiglianza del coseno" o "distanza del coseno" per indicare la differenza tra l'orientamento di due vettori. Ad esempio, quanto vi girereste per affrontare la porta d'ingresso?
Fatto divertente e applicabile: nonostante il fatto che "somiglianza" e "distanza" abbiano significati diversi da soli, l'aggiunta del coseno prima di entrambi i termini li fa significare quasi la stessa cosa! Questo è un altro esempio di somiglianza semantica.
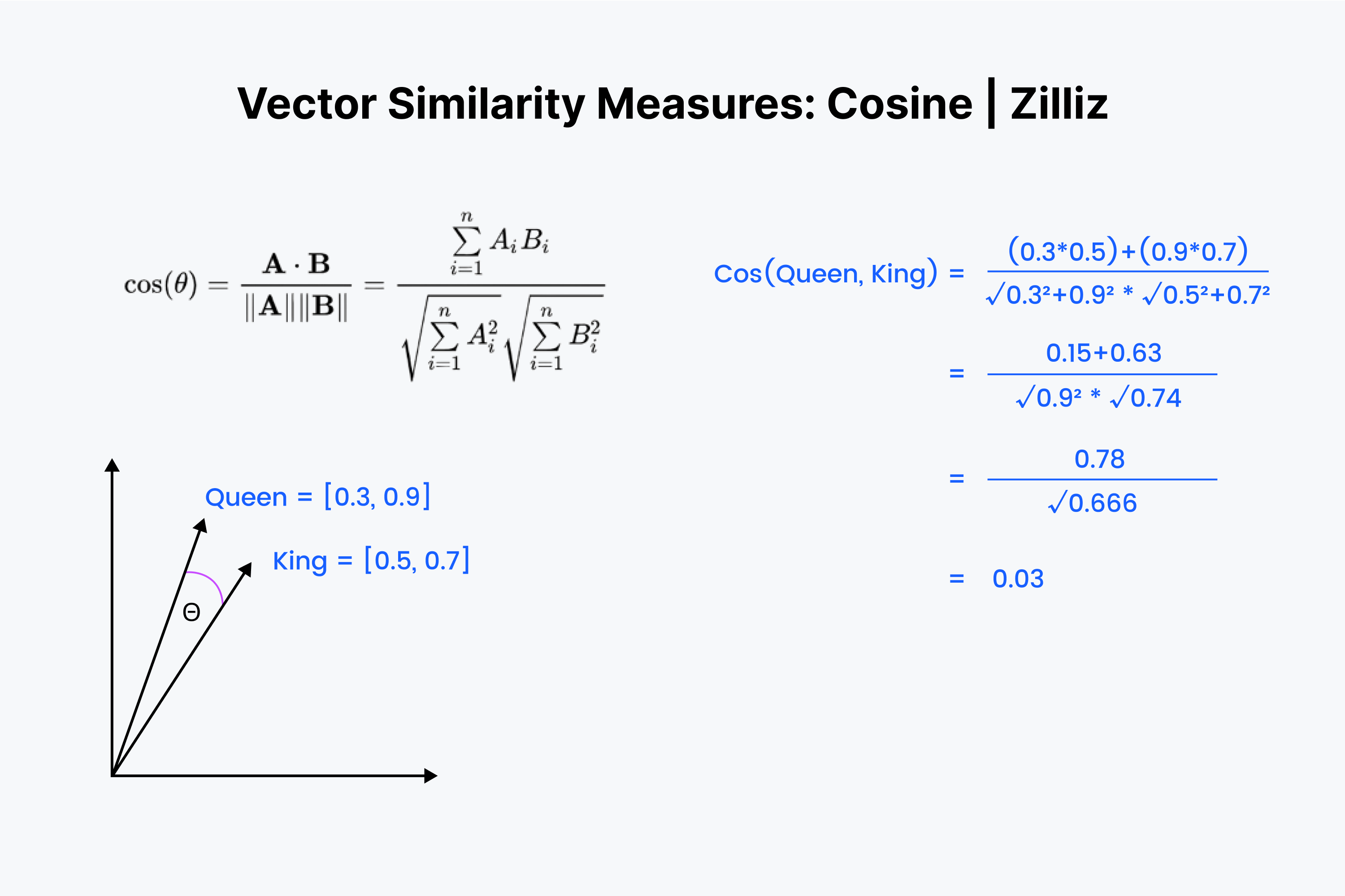
Sappiamo quindi che la somiglianza del coseno misura l'angolo tra due vettori. Ancora una volta, immaginiamo i nostri vettori come un elenco di numeri. Questa volta, però, il processo è un po' più complesso.
Cominciamo ad allineare di nuovo i vettori l'uno sull'altro. Si inizia moltiplicando i numeri e poi sommando tutti i risultati. Ora salviamo questo numero; chiamiamolo "x". Successivamente, dobbiamo elevare al quadrato ogni numero e sommare i numeri di ciascun vettore. Immaginate di squadrare ogni numero in orizzontale e di sommarli per entrambi i vettori.
Prendiamo la radice quadrata di entrambe le somme, poi moltiplichiamole e chiamiamo questo risultato "y". Il valore della distanza coseno è dato da "x" diviso per "y".
La somiglianza del coseno è utilizzata principalmente nelle [applicazioni NLP] (https://zilliz.com/learn/top-5-nlp-applications). L'elemento principale che misura la somiglianza coseno è la differenza di orientamento semantico. Se si lavora con vettori normalizzati, la somiglianza coseno è equivalente al prodotto interno.
Il prodotto interno è la proiezione di un vettore sull'altro. Il valore del prodotto interno è la lunghezza del vettore estratto. Più grande è l'angolo tra i due vettori, più piccolo è il prodotto interno. Inoltre, il prodotto interno cresce con la lunghezza del vettore più piccolo. Pertanto, utilizziamo il prodotto interno quando ci interessano l'orientamento e la distanza. Ad esempio, per raggiungere il frigorifero si deve percorrere una distanza rettilinea attraverso le pareti.
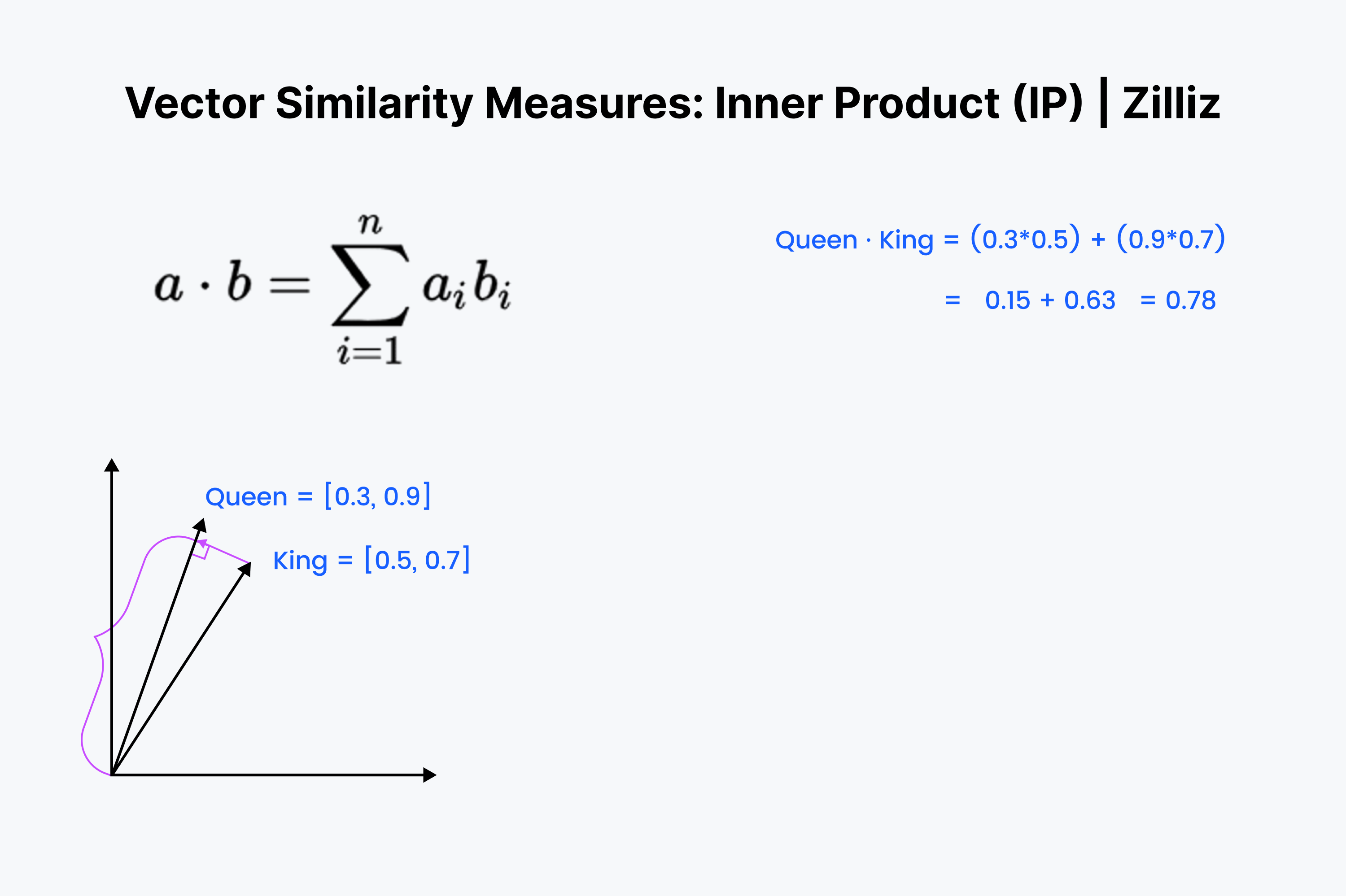
Il prodotto interno dovrebbe risultare familiare. È solo il primo ⅓ del calcolo del coseno. Allineate i vettori nella vostra mente e scendete lungo la riga, moltiplicando verso il basso. Poi, sommateli. Questo misura la distanza in linea retta tra voi e la somma dim più vicina.
Il prodotto interno è un incrocio tra la distanza euclidea e la somiglianza del coseno. Quando si tratta di set di dati normalizzati, è uguale alla somiglianza del coseno, quindi IP è adatto a set di dati normalizzati o non normalizzati. È un'opzione più veloce della somiglianza cosinica e più flessibile.
Una cosa da tenere presente con il Prodotto interno è che non segue la disuguaglianza dei triangoli. Le lunghezze maggiori (grandi grandezze) hanno la priorità. Questo significa che bisogna fare attenzione quando si usa IP con Inverted File Index o un indice grafico come HNSW.
Le tre metriche vettoriali sopra menzionate sono le più utili per quanto riguarda vector embeddings. Tuttavia, non sono gli unici modi per misurare la distanza tra due vettori. Ecco altri due modi per misurare la distanza o la somiglianza tra vettori.
Gruppo 13401.png
La distanza di Hamming può essere applicata a vettori o a stringhe. Per i nostri casi d'uso, ci limitiamo ai vettori. La distanza di Hamming misura la "differenza" tra gli entri di due vettori. Ad esempio, "1011" e "0111" hanno una distanza di Hamming pari a 2.
In termini di incorporazioni vettoriali, la distanza di Hamming ha senso misurarla solo per i vettori binari. Le [Float vector embeddings] (https://youtube.com/shorts/d_XNrd8PrTc?feature=share), le uscite del penultimo livello delle reti neurali, sono costituite da numeri in virgola mobile compresi tra 0 e 1. Alcuni esempi possono essere [0.24, 0.111, 0.21, 0.51235] e [0.33, 0.664, 0.125152, 0.1].
Come si può notare, la distanza di Hamming tra due incorporazioni vettoriali sarà quasi sempre pari alla lunghezza del vettore stesso. Ci sono troppe possibilità per ogni valore. Ecco perché la distanza di Hamming può essere applicata solo a vettori binari o radi. Il tipo di vettori prodotti da un processo come TF-IDF, BM25 o SPLADE.
La distanza di Hamming è ottima per misurare qualcosa come la differenza di formulazione tra due testi, la differenza nell'ortografia delle parole o la differenza tra due vettori binari. Ma non va bene per misurare la differenza tra le incorporazioni di vettori.
Ecco un fatto divertente. La distanza di Hamming è equivalente alla somma del risultato di un'operazione XOR su due vettori.
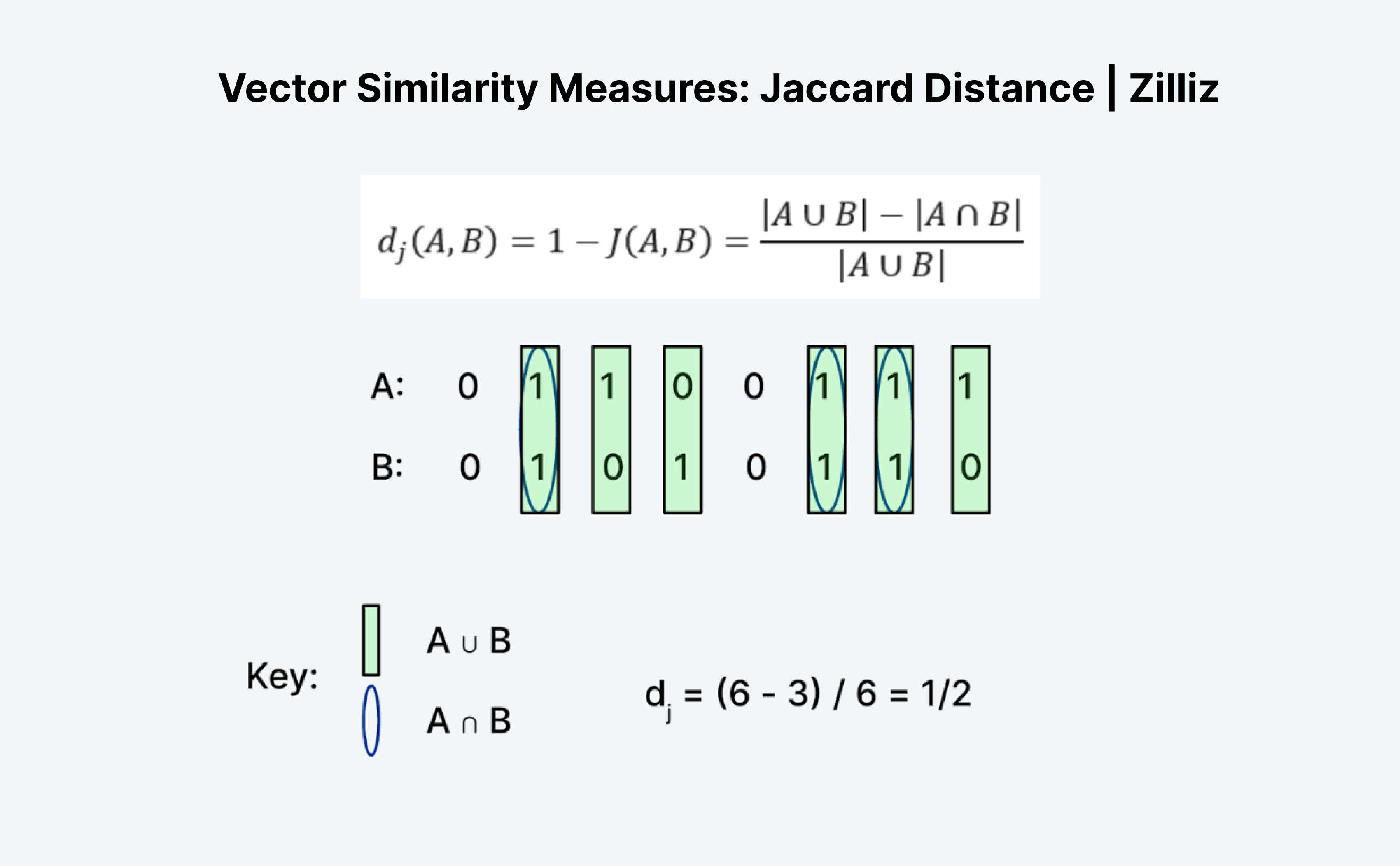
La distanza di Jaccard è un altro modo per misurare la somiglianza o la distanza di due vettori. L'aspetto interessante di Jaccard è che esistono sia un indice di Jaccard sia una distanza di Jaccard. La distanza di Jaccard è 1 meno l'indice di Jaccard, la metrica di distanza che Milvus implementa.
Il calcolo della distanza o dell'indice di Jaccard è un compito interessante perché a prima vista non ha molto senso. Come la distanza di Hamming, Jaccard funziona solo su dati binari. La formazione tradizionale di "unioni" e "intersezioni" mi confonde. Il mio modo di pensare è quello della logica. È essenzialmente A "OR" B meno A "AND" B diviso per A "OR" B.
Come mostrato nell'immagine precedente, contiamo il numero di voci in cui A o B sono 1 come "unione" e in cui sia A che B sono 1 come "intersezione". Quindi l'indice di Jaccard per A (01100111) e B (01010110) è ½. In questo caso, anche la distanza di Jaccard, 1 meno l'indice di Jaccard, è ½.
In questo post abbiamo imparato a conoscere le tre metriche di ricerca della similarità vettoriale più utili: La distanza L2 (nota anche come distanza euclidea), la distanza coseno e il prodotto interno. Ognuna di queste ha casi d'uso diversi. La distanza euclidea serve quando ci interessa la differenza di grandezza. Il coseno serve quando ci interessa la differenza di orientamento. Il prodotto interno è utile quando ci interessa la differenza di grandezza e di orientamento.
Guardate questi video per saperne di più sulle metriche di somiglianza vettoriale, oppure leggete i documenti per imparare a configurare queste metriche in Milvus.
Introduzione alle metriche di somiglianza
Le metriche di somiglianza sono uno strumento fondamentale in varie attività di analisi dei dati e di apprendimento automatico. Ci permettono di confrontare e valutare la somiglianza tra diversi dati, facilitando applicazioni come il clustering, la classificazione e le raccomandazioni. Con numerose metriche di somiglianza disponibili, ognuna con i suoi punti di forza e di debolezza, la scelta di quella giusta per un compito specifico può essere impegnativa. In questa sezione introdurremo il concetto di metriche di similarità, la loro importanza e forniremo una panoramica delle metriche più comunemente utilizzate.
Similitudine del coseno
La somiglianza coseno è una metrica di somiglianza molto utilizzata che misura il coseno dell'angolo tra due vettori. È comunemente utilizzata nell'elaborazione del linguaggio naturale e nelle attività di information retrieval. La metrica della somiglianza del coseno è particolarmente utile quando si tratta di dati ad alta dimensionalità, in quanto è efficiente dal punto di vista computazionale e può gestire dati sparsi. La somiglianza del coseno tra due vettori può essere calcolata utilizzando il prodotto del punto dei vettori diviso per il prodotto delle loro grandezze.
Distanza euclidea
La distanza euclidea, nota anche come distanza rettilinea, è una metrica di distanza ampiamente utilizzata che misura la distanza tra due punti nello spazio n-dimensionale. È calcolata come la radice quadrata della somma delle differenze al quadrato tra gli elementi corrispondenti dei due vettori. La distanza euclidea è comunemente utilizzata in varie applicazioni, tra cui il clustering, la classificazione e l'analisi di regressione. Tuttavia, può essere sensibile agli outlier e può non funzionare bene con i dati ad alta dimensionalità.
Scegliere la giusta metrica di somiglianza
La scelta della giusta metrica di similarità dipende da vari fattori, tra cui il tipo di dati, gli obiettivi dell'analisi e la relazione tra le variabili. Ad esempio, la somiglianza del coseno è adatta per i dati ad alta dimensione e per le attività di elaborazione del linguaggio naturale, mentre la distanza euclidea è comunemente utilizzata per le attività di clustering e classificazione. La distanza di Manhattan, nota anche come distanza L1, è adatta ai dati con outlier, mentre la distanza di Hamming è utilizzata per i dati binari. È essenziale comprendere le caratteristiche e i limiti di ciascuna metrica di similarità per scegliere quella più appropriata per un compito specifico.
Applicazioni del mondo reale
Le metriche di similarità hanno numerose applicazioni reali in vari campi, tra cui:
Elaborazione del linguaggio naturale: La somiglianza del coseno è ampiamente utilizzata nella classificazione dei testi, nell'analisi del sentiment e nel reperimento di informazioni.
Sistemi di raccomandazione: Le metriche di somiglianza, come la somiglianza del coseno e la distanza euclidea, sono utilizzate per raccomandare prodotti o servizi in base al comportamento e alle preferenze degli utenti.
Analisi di immagini e video: Le metriche di somiglianza, come la distanza euclidea e la distanza di Manhattan, sono utilizzate nella classificazione di immagini e video, nel [rilevamento di oggetti] (https://zilliz.com/learn/what-is-object-detection) e nelle attività di tracciamento.
Clustering e classificazione: Le metriche di somiglianza, come la distanza euclidea e la somiglianza coseno, sono utilizzate nelle attività di clustering e classificazione per raggruppare punti di dati simili.
In conclusione, le metriche di somiglianza sono uno strumento cruciale in varie attività di analisi dei dati e di apprendimento automatico. Comprendere le caratteristiche e i limiti di ciascuna metrica di similarità è essenziale per scegliere quella più appropriata per un compito specifico. Selezionando la metrica di similarità giusta, possiamo migliorare l'accuratezza e la pertinenza dei nostri risultati, portando a migliori decisioni e approfondimenti.
Yujian TangYujian Tang is a Developer Advocate at Zilliz. He has a background as a software engineer working on AutoML at Amazon. Yujian studied Computer Science, Statistics, and Neuroscience with research papers published to conferences including IEEE Big Data. He enjoys drinking bubble tea, spending time with family, and being near water.
- Introduzione alle metriche di somiglianza
- Similitudine del coseno
- Distanza euclidea
- Scegliere la giusta metrica di somiglianza
- Applicazioni del mondo reale
Contenuto
Inizia gratis, scala facilmente
Prova il database vettoriale completamente gestito progettato per le tue applicazioni GenAI.
Prova Zilliz Cloud gratuitamenteContinua a leggere
Why and How to Migrate from Self-Hosted Milvus to Zilliz Cloud
A simple, step-by-step guide to migrating from Milvus to Zilliz Cloud. Learn both endpoint and backup methods for a smooth, scalable vector database migration.
Vector Databases vs. Hierarchical Databases
Use a vector database for AI-powered similarity search; use a hierarchical database for organizing data in parent-child relationships with efficient top-down access patterns.
RocketQA: Optimized Dense Passage Retrieval for Open-Domain Question Answering
RocketQA is a highly optimized dense passage retrieval framework designed to enhance open-domain question-answering (QA) systems.